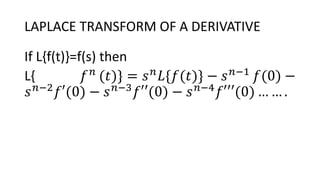The document discusses the Laplace transformation and its properties. The Laplace transformation takes a function of time and transforms it into a function of a complex variable. Some key properties are the shifting property, division property, and the property regarding the Laplace transform of a derivative. The Laplace transformation is useful for solving differential equations and has applications in fields like engineering and signal processing. It was invented by Pierre-Simon Laplace and further developed by Oliver Heaviside.

1. LAPLACE TRANSFORMATION
& IT’S PROPERTIES
NAME :- AANCHAL SINGH
CLASS :- M.Sc. I YEAR (SEMESTER-I)
COLLEGE :–VMV COLLEGE,WARDHAMAN
NAGAR,NAGPUR

2. CONTENT
• INTRODUCTION
• LAPLACE TRANSFORMATION
• PROPERTIES
1)SHIFTING PROPERTY
2)DIVISION PROPERTY
3)TRANSFORM OF INTEGRAL
4)MULTIPLICATION PROPERTY
5)LAPLACE TRANSFORM OF A DERIVATIVE
• APPLICATION

3. HISTORY OF LAPLACE TRANSFORMATION
SYSTEMATICALLY DEVELOPED BY:
BRITISH PHYSICIST
OLIVER
HEAVISIDE
(1850-1925)
INVENTED BY:
FRENCH MATHEMATICIAN
PIERRE-SIMON
LAPLACE
(1749-1827)

4. LAPLACE TRANSFORMATION
Let f(t) be a function of ‘t’defined for all positive
values of ‘t’ ,then the LAPLACE TRANSFORM of
f(t) denoted by L{f(t)} is defined by
𝐿 𝑓 𝑡 = 0
∞
𝑒−𝑠𝑡
.f(t)dt
Provided the integral exist
Where s- parameter which may be real or
complex no.

5. PROPERTIES
1)SHIFTING PROPERTY
If L{F(t)}=f(s) then
L{ 𝑒𝑎𝑡
. 𝐹(𝑡)} = 𝑓(𝑠 − 𝑎)
Ex: 𝑒−2𝑡
sin3t=
3
𝑠2+4𝑠+13

6. DIVISION PROPERTY
If L{f(t)}=f(s) then
L{
1
𝑡
.F(t)}= 𝑠
∞
𝑓 𝑠 𝑑𝑠
L{
𝑠𝑖𝑛𝑡
𝑡
}= 𝑠
∞ 1
𝑠2+1
ds
=𝑐𝑜𝑡−1
s

7. TRANSFORM OF INTEGRAL
If L{f(t)}=f(s) then
L{ 0
𝑡
𝐹 𝑡 𝑑𝑡} =
1
𝑆
𝑓(𝑠)

8. MULTIPLICATION PROPERTY
If L{f(t)}=f(s) then
L{𝑡𝑛
. 𝐹(𝑡)} = (−1)𝑛 𝑑𝑛
𝑑𝑠𝑛[f(s)]
L{t.sin3t}=(−1)1 𝑑
𝑑𝑠
(
3
𝑠2+9
)
=
6𝑠
(𝑠2+9)2

9. LAPLACE TRANSFORM OF A DERIVATIVE
If L{f(t)}=f(s) then
L{ 𝑓𝑛
(𝑡)} = 𝑠𝑛
𝐿{𝑓(𝑡)} − 𝑠𝑛−1
𝑓(0) −
𝑠𝑛−2𝑓′(0) − 𝑠𝑛−3𝑓′′(0) − 𝑠𝑛−4𝑓′′′(0) … … .

10. APPLICATION
• It is used to convert complex differential equation to a
simpler form having polynomials.
• It is used in the telecommunication field to send signals to
both the sides of the medium.
• It is also used for many engineering task such as Electrical
Circuit Analysis,Digital Signal Processing,System
Modelling,etc.
• Laplace Transform is widely used by electronic engineers to
solve quickly differential equations occurring in the analysis
of electronic circuits.

11. CREATED BY:-
AANCHAL SINGH