Uploaded bygoehnert
1,601 views

LAK13 Tutorial Social Network Analysis 4 Learning Analytics

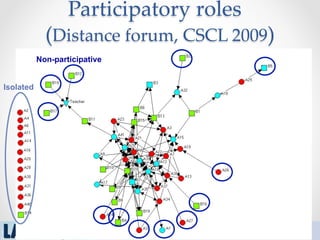
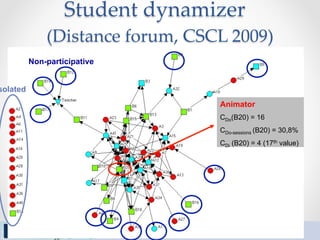
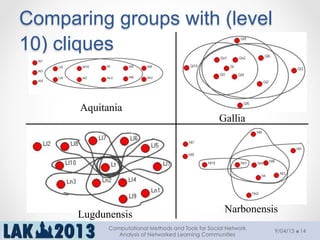
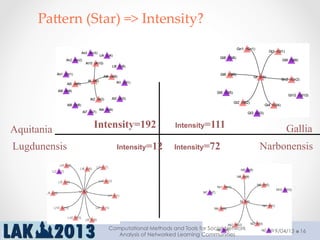
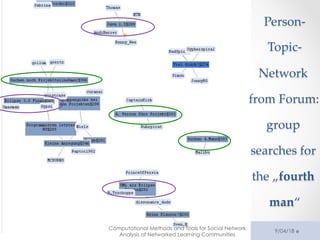
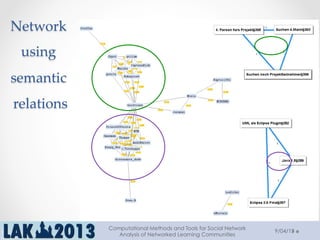
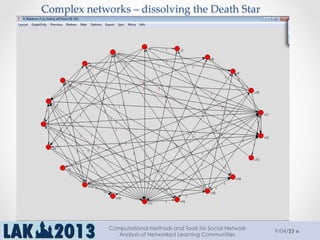
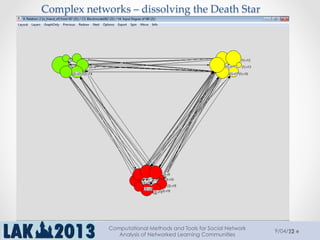
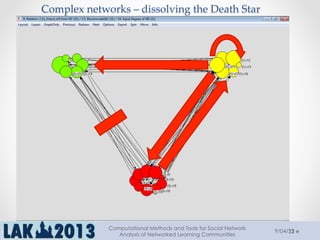
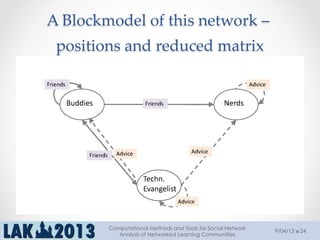
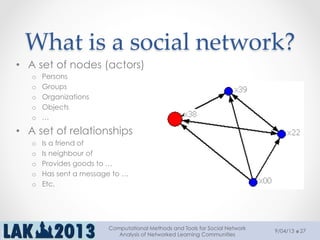
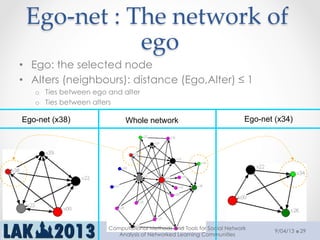
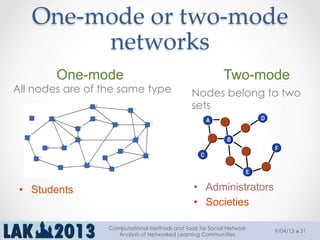
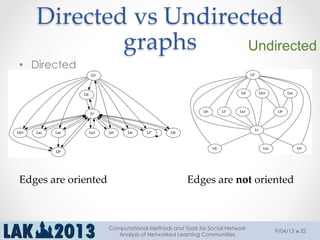
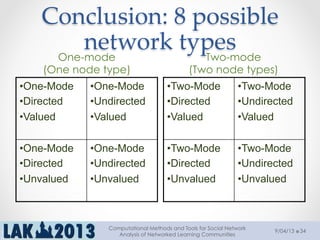
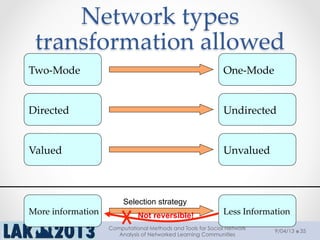
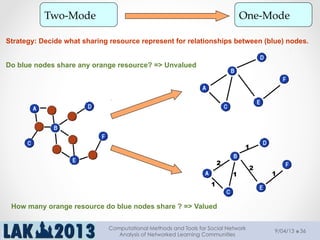
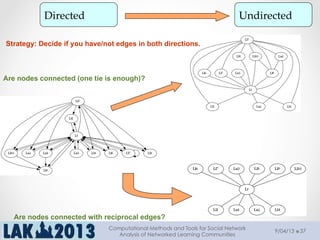
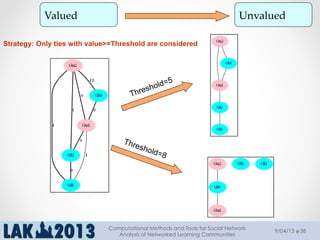
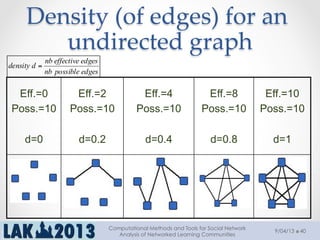
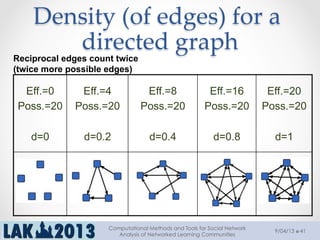
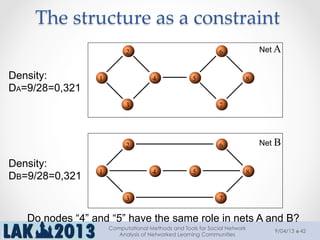
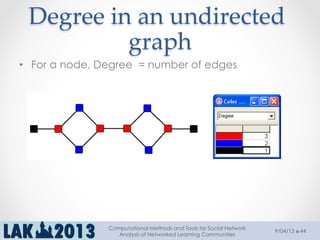
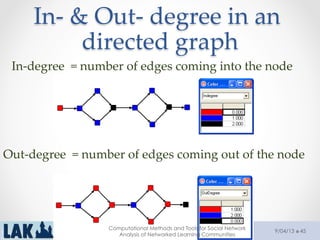
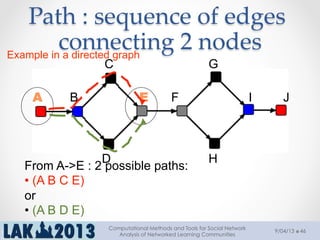
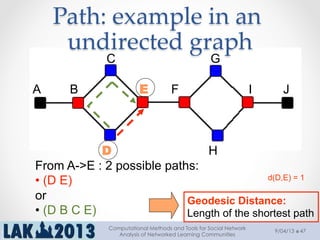
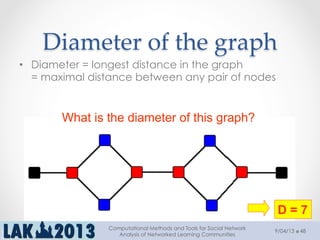
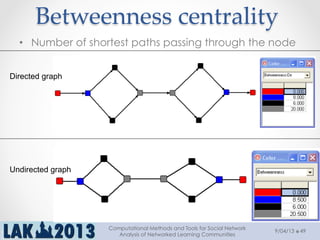
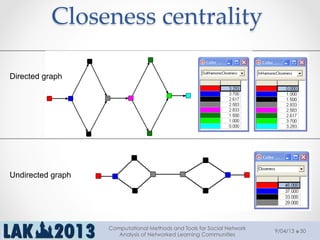
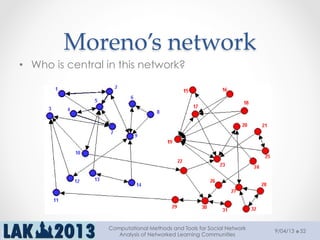
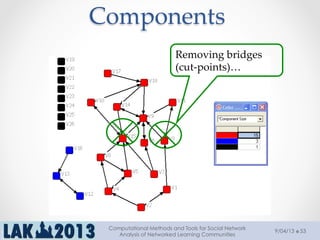
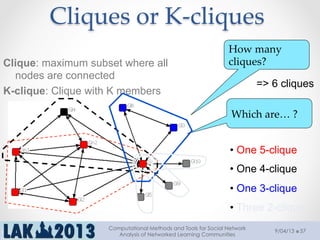
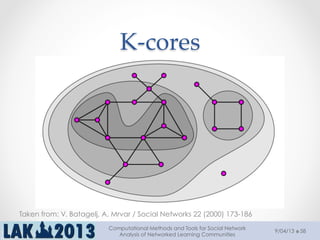
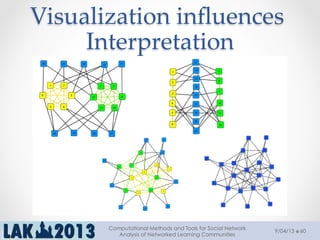
The document outlines a tutorial on computational methods and tools for social network analysis (SNA) conducted at LAK 2013, covering topics such as participatory roles, cohesion in online groups, and various SNA basics including types and transformations of social networks. It introduces specific use cases and technical measures such as centrality, path distances, and density relevant to network analysis. Participants were engaged through hands-on experiences using a practical workbench for SNA application in networked learning communities.

Embed presentation

Computational  Methods   and  Tools  for  Social   Network  Analysis  of   Networked  Learning   Communities Tutorial at LAK 2013, 9/4/2013 Andreas Harrer, Tilman Göhnert, Alejandra Martínez-Monés & Christophe Reffay
Agenda 13.30 Introduction of presenters and participants 13.45 Use Cases of SNA4LA 14.15 SNA Basics 15.15 Description of the practical workbench 15.30 COFFEE BREAK 16.00 Hands-on experiences using the workbench 17.30 End of the tutorial 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 2
Introduction  of  presenters   &  participants 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 3
Tutorial  Presenters •  Andreas Harrer •  Tillman Göhnert •  Alejandra Martínez-Monés •  Christophe Reffay 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 4
Use  Cases  of  SNA  for  LA 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 5
Identifying  Participatory   Roles  in  CSCL  scenarios Marcos García, J.A.,  Martínez Monés, A.,  Dimitriadis, Y.,  Anguita Martínez, R. A role-based approach for the support of collaborative learning activities e-Service Journal. 6(1):40-58, Diciembre 2007 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 6
Participatory  roles •  Goal: Identifying roles based on their position within a network of relationships o  Description of expected roles, based on centrality indexes o  Identify the emergence of those roles in an experience o  Provide them with information adapted to their needs •  Approach: o  Description of roles based on “fuzzy” combinatios of SNA indexes 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 7
Participatory  roles     (Distance  forum,  CSCL  2009) Isolated Non-participative
Role: Dynamizer student Indicators Outdegree CDo(i) Description Number of links initiated by this actor. V a l u e s / Interpretation A high value, indicates a high participation of the actor R e l e v a n c e rank First Outdegree sessions Description Specifies the relation between participation and number of sessions V a l u e s / Interpretation A high value indicates a high participation of the actor in the overall activity R e l e v a n c e rank Second Indegree CDi(i) Description Number of links terminating by this actor V a l u e s / Interpretation A medium value indicates a medium relevance R e l e v a n c e rank Third. Participatory  roles   Dynamizer  student 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 9
Student  dynamizer     (Distance  forum,  CSCL  2009) Animator CDo(B20) = 16 CDo-sessions (B20) = 30,8% CDi (B20) = 4 (17th value) solated Non-participative
Student  dynamizer     (Web-­‐‑based  document  sharing) 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 11 aalobel abalarr aordboa arodull cfergon cgeiveg cgonzrol cjimcab emonveg emunsei epadgon esasbaz estibaliz ggj ibalala ilizmar imunado jjimrio jorge lcaravi lconase lhergar Lmunbla marnmar Mcamalo mferrub mlauroth mmaygom mmiggut ncalgua Noelia papajim plagvel ppersan profe rapaduq rfueote rgorvil rmarcol rpermar Rumbram scilram scunfer sfermar smarmor vdiefer Vmaybar Animator
Cohesion  in  subgroups   Reffay, C. and Chanier, T., (2003) How social network analysis can help to measure cohesion in collaborative distance learning, Proc of CSCL, 2003 Reffay, C., Teplovs, C., & Blondel, F.-M. (2011). Productive re- use of CSCL data and analytic tools to provide a new perspective on group cohesion. Proc of CSCL 2011. 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 12
Cohesion •  Simugline data set o  4 online groups working on an French as foreign language simulation o  Each group had an instructor and a •  Data o  Discussion forums that are local to each of the 4 groups •  Network o  The relation between “a” and “b” represents messages sent by “a” and opened by “b” plus messages posted by “b” and opened by “a” •  Indexes o  Cliques at level “c”: subgroup in which the ties between all pairs of agents have values c or greater (i.e., have exchanged c or more messages). o  “c” can be a value announced by the teacher as the desirable level of interaction 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 13
Comparing groups with (level 10) cliques Aquitania Gallia Lugdunensis Gallia Narbonensis 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 14
Hierarchical Clusters GALLIA G G G G G G G G G G l l l n l G l n l l l 1 Level 3 2 1 1 t 4 2 6 5 9 0 ----- - - - - - - - - - - - 167 . . . XXX . . . . . . 108 . . . XXXXX . . . . . 83 . . XXXXXXX . . . . . 64 . . XXXXXXXXX . . . . 52 . XXXXXXXXXXX . . . . 42 XXXXXXXXXXXXX . . . . 29 XXXXXXXXXXXXXXX . . . 9 XXXXXXXXXXXXXXX XXXXX 5 XXXXXXXXXXXXXXXXXXXXX 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 15
PaNern  (Star)  =>  Intensity? Aquitania Lugdunensis Narbonensis GalliaIntensity=192 Intensity=12 Intensity=72 Intensity=111 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 16
The  “fourth”  man Malzahn, N., Harrer, A., & Zeini, S. (2007). The Fourth Man - Supporting self-organizing group formation in learning communities. In Proc. of CSCL 2007 (pp. 547–550). 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 17
18 Person-­‐‑ Topic-­‐‑ Network   from  Forum:   group   searches  for   the  „fourth   man“ 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
19 Network   using   semantic   relations 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
Blockmodeling Harrer, A. & Schmidt, A. (to appear 2013). Blockmodeling and role analysis in multi-relational networks. Social Networks and Mining. Springer. 2013 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 20
21 Complex  networks  –  dissolving  the  Death  Star 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
22 Complex  networks  –  dissolving  the  Death  Star 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
23 Complex  networks  –  dissolving  the  Death  Star 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
A  Blockmodel  of  this  network  –   positions  and  reduced  matrix 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 24
SNA  basics 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 25
SNA  basics •  What is a Social Network? •  Types of networks and network transformations •  Useful definitions and measures on graphs •  Grouping concepts 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 26
What  is  a  social  network? •  A set of nodes (actors) o  Persons o  Groups o  Organizations o  Objects o  … •  A set of relationships o  Is a friend of o  Is neighbour of o  Provides goods to … o  Has sent a message to … o  Etc. 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 27
What  is  a  social  network? •  Complexity may increase. •  Analysis cannot be done by hand 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 28
Ego-­‐‑net  :  The  network  of   ego •  Ego: the selected node •  Alters (neighbours): distance (Ego,Alter) ≤ 1 o  Ties between ego and alter o  Ties between alters Whole network Ego-net (x34)Ego-net (x38) 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 29
Types  of  Social  Networks   According  to… •  Number of sets of actors o  One-mode : one set of actors o  Two-mode : (Bi-partite, affiliation networks) two sets of actors •  Relationships o  Directed or undirected o  Valued or un-valued (1/0) •  How are they built o  Complete networks o  Ego-networks 9/04/13Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 3030
One-­‐‑mode  or  two-­‐‑mode   networks All nodes are of the same type •  Administrators •  Societies Two-modeOne-mode 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 31 Nodes belong to two sets •  Students
Directed  vs  Undirected   graphs •  Directed Undirected Edges  are  oriented Edges  are  not  oriented 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 32
Weighted  (valued)  vs   Unvalued  graphs •  Weighted/Valued •  Unvalued Edges  have  values Edges  have  no  value 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 33
Conclusion:  8  possible   network  types One-mode (One node type) Two-mode (Two node types) • One-Mode • Directed • Valued • One-Mode • Undirected • Valued • One-Mode • Directed • Unvalued • One-Mode • Undirected • Unvalued • Two-Mode • Directed • Valued • Two-Mode • Undirected • Valued • Two-Mode • Directed • Unvalued • Two-Mode • Undirected • Unvalued 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 34
Network  types   transformation  allowed Two-­‐‑Mode One-­‐‑Mode Directed Undirected Valued Unvalued More  information Less  Information Selection strategy Not reversible! 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 35
Two-­‐‑Mode One-­‐‑Mode 2 2 1 1 1 1 Do blue nodes share any orange resource? => Unvalued How many orange resource do blue nodes share ? => Valued Strategy: Decide what sharing resource represent for relationships between (blue) nodes. 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 36
Directed Undirected Are nodes connected (one tie is enough)? Are nodes connected with reciprocal edges? Strategy: Decide if you have/not edges in both directions. 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 37
Valued Unvalued Threshold=5 Strategy: Only ties with value>=Threshold are considered 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 38
Useful  measures  of  social   networks •  Density •  Degree, In-degree, Out-degree •  Path, Geodesic distance, Diameter •  Centrality indexes (for nodes) o  Degree centrality o  Betweenness centrality, o  Closeness centrality 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 39
Eff.=0 Poss.=10 d=0 Eff.=2 Poss.=10 d=0.2 Eff.=4 Poss.=10 d=0.4 Eff.=8 Poss.=10 d=0.8 Eff.=10 Poss.=10 d=1 Density  (of  edges)  for  an   undirected  graph edgespossiblenb edgeseffectivenb ddensity = 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 40
Density  (of  edges)  for  a   directed  graph Eff.=0 Poss.=20 d=0 Eff.=4 Poss.=20 d=0.2 Eff.=8 Poss.=20 d=0.4 Eff.=16 Poss.=20 d=0.8 Eff.=20 Poss.=20 d=1 Reciprocal edges count twice (twice more possible edges) 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 41
1 4 2 6 5 8 3 7 Net A 1 2 4 5 6 8 3 7 Net B The  structure  as  a  constraint   Do nodes “4” and “5” have the same role in nets A and B? Density: DA=9/28=0,321 Density: DB=9/28=0,321 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 42
Centrality •  Who is central in this network? 439/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
Degree  in  an  undirected   graph •  For a node, Degree = number of edges 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 44
In-­‐‑  &  Out-­‐‑  degree  in  an   directed  graph In-­‐‑degree    =  number  of  edges  coming  into  the  node Out-­‐‑degree    =  number  of  edges  coming  out  of  the  node 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 45
Path  :  sequence  of  edges   connecting  2  nodes A H B C G D E F I J From A->E : 2 possible paths: • (A B C E) or • (A B D E) Example in a directed graph 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 46
Path:  example  in  an   undirected  graph A H B C G D E F I J From A->E : 2 possible paths: • (D E) or • (D B C E) Geodesic Distance: Length of the shortest path d(D,E) = 1 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 47
Diameter  of  the  graph •  Diameter = longest distance in the graph = maximal distance between any pair of nodes What is the diameter of this graph? D = 7 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 48
Betweenness  centrality   •  Number of shortest paths passing through the node Directed graph Undirected graph 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 49
Closeness  centrality   Scoring the closeness of one node to all others Undirected graph Directed graph 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 50
The Moreno’s experiments (1943) Pupils relation in the classroom: •  Pupils of various age range •  Gender study « If you could choose freely, which are the (2) kids you would like to have as direct neighbour? » Main results: At <age> => pupils tend to <?> • 6-8 years old => mix • 8-13 years old => separate • 13-15 years old => mix • 15-17 years old => separate 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 51
Moreno’s  network •  Who is central in this network? 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 52
Components   Removing  bridges     (cut-­‐‑points)… 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 53
…This  results  in  breaking   the  component   9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 54
Grouping  concepts  –  an   overview Groups can be determined according to different criteria •  Reachability and Distance – group member is connected via short ways to all other group members o  Direct links – Clique as complete subgraph o  Relaxing the distance – n-Clique requires all nodes being connected via short path (lesser and equal than n) •  Node degree – group member should be connected to many group members o  Leaving out a small number of group members: k-Plex o  Having at least k group members as direct neighbours – k-Core •  Contrasting “ingroup” and “outgroup” – density inside is much higher than outside o  Alliance: only links to ingroup, no links to outside 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 55
Grouping  concepts  –  an   overview •  Group concepts fall in two categories: o  Overlapping concepts •  e.g. Cliques o  Disjunct concepts •  e.g. k-cyclic blocks •  Depending on the type of analysis both categories have their merits o  Disjunct concepts allow clear-cut assignment to one group o  Overlapping concepts allow analysis of transfer ideas, e.g. Clique percolation 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 56
Cliques  or  K-­‐‑cliques   Clique: maximum subset where all nodes are connected K-clique: Clique with K members How  many     cliques? • One 5-clique • One 4-clique • One 3-clique • Three 2-cliques => 6 cliques Which  are…  ? 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 57
K-­‐‑cores 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 58 Taken from: V. Batagelj, A. Mrvar / Social Networks 22 (2000) 173-186
Clique  Percolation   Method •  CPM allows overlapping communities •  Idea: a k-clique “percolates” through the graph •  Overlapping members can be “brokers” between groups 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 59 Taken from: Wikipedia
Visualization  influences   Interpretation 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 60
Practical  Workbench     Presentation 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 61
Task  one:  Simuligne   Data  Preprocessing 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 62 Raw Data: A network with weighted, directed edges (Number of forum posts opened) Preprocessing: Symmetrisation of edge weights (by minimum, maximum, sum, or average)
Task  one:  Simuligne •  Choose the data set based on preprocessing o  Narbo_Max: Maximum of both directions o  Narbo_Mean: Average of both directions o  Narbo_Min: Minimum of both directions o  Narbo_Sum: Sum of both directions •  Think of the format transformation (UCINET -> SISOB) •  Focus on the appropriate intensity level of the relation •  Identify groups •  Choose an appropriate output representation 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 63
Task  two:  Collaboration   over  Artifacts  (BSCW) 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 64 •  Two node types o  BSCW (document sharing) folders as artifacts (-..) •  One folder for general information •  Folders for individual case studies o  Pairs of students, each working mainly on a single case (x..) •  Edges weighted by access
Task  two:  Collaboration   over  Artifacts  (BSCW) 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 65 •  Choose one of the data sets o  sp1_B_cli_cp_U.txt o  sp2_B_cli_cp_U.txt o  sp3_B_cli_cp_U.txt o  spf_B_cli_cp_U.txt •  Think of the format transformation (UCINET -> SISOB) •  Try to identify the general folder •  Try to identify the projects the pairs of students worked on •  Analyse the collaboration between the students (hint: Folding is also in the R-Analysis)

More Related Content

PPT
Social Network Analysis
byGiorgos Cheliotis
 
PPTX
Social Network Analysis: What It Is, Why We Should Care, and What We Can Lear...
byXiaohan Zeng
 
PDF
Network Visualization guest lecture at #DataVizQMSS at @Columbia / #SNA at PU...
byDenis Parra Santander
 
PPTX
Social network analysis
byWorld Agroforestry (ICRAF)
 
PDF
Social network analysis intro part I
byTHomas Plotkowiak
 
PDF
Preso on social network analysis for rtp analytics unconference
byBruce Conner
 
PPT
Making the invisible visible through SNA
byMYRA School of Business
 
PPTX
Social Network Analysis Workshop
byData Works MD
 
Social Network Analysis
byGiorgos Cheliotis
 
Social Network Analysis: What It Is, Why We Should Care, and What We Can Lear...
byXiaohan Zeng
 
Network Visualization guest lecture at #DataVizQMSS at @Columbia / #SNA at PU...
byDenis Parra Santander
 
Social network analysis
byWorld Agroforestry (ICRAF)
 
Social network analysis intro part I
byTHomas Plotkowiak
 
Preso on social network analysis for rtp analytics unconference
byBruce Conner
 
Making the invisible visible through SNA
byMYRA School of Business
 
Social Network Analysis Workshop
byData Works MD
 

What's hot

PPT
How to conduct a social network analysis: A tool for empowering teams and wor...
byJeromy Anglim
 
PPT
Overview Of Network Analysis Platforms
byNoah Flower
 
PPTX
Social Network Analysis
byFred Stutzman
 
PDF
Subscriber Churn Prediction Model using Social Network Analysis In Telecommun...
byBAINIDA
 
PPT
The Basics of Social Network Analysis
byRory Sie
 
PPTX
Social Network Analysis (SNA) 2018
byArsalan Khan
 
PPTX
Social Network Analysis
byScott Gomer
 
PPTX
Social Network Analysis power point presentation
byRatnesh Shah
 
PPT
01 Introduction to Networks Methods and Measures
bydnac
 
PPTX
A Guide to Social Network Analysis
byOlivier Serrat, PhD
 
PPTX
01 Network Data Collection (2017)
byDuke Network Analysis Center
 
PPTX
03 Communities in Networks (2017)
byDuke Network Analysis Center
 
PPTX
Social Network Analysis Introduction including Data Structure Graph overview.
byDoug Needham
 
PPT
Social network analysis course 2010 - 2011
byguillaume ereteo
 
PPT
2009 Node XL Overview: Social Network Analysis in Excel 2007
byMarc Smith
 
PDF
Social Network Analysis
bySujoy Bag
 
PDF
Big social data analytics - social network analysis
byJari Jussila
 
PPTX
02 Descriptive Statistics (2017)
byDuke Network Analysis Center
 
PDF
Social network analysis & Big Data - Telecommunications and more
byWael Elrifai
 
PDF
Exploring Social Media with NodeXL
byShalin Hai-Jew
 
How to conduct a social network analysis: A tool for empowering teams and wor...
byJeromy Anglim
 
Overview Of Network Analysis Platforms
byNoah Flower
 
Social Network Analysis
byFred Stutzman
 
Subscriber Churn Prediction Model using Social Network Analysis In Telecommun...
byBAINIDA
 
The Basics of Social Network Analysis
byRory Sie
 
Social Network Analysis (SNA) 2018
byArsalan Khan
 
Social Network Analysis
byScott Gomer
 
Social Network Analysis power point presentation
byRatnesh Shah
 
01 Introduction to Networks Methods and Measures
bydnac
 
A Guide to Social Network Analysis
byOlivier Serrat, PhD
 
01 Network Data Collection (2017)
byDuke Network Analysis Center
 
03 Communities in Networks (2017)
byDuke Network Analysis Center
 
Social Network Analysis Introduction including Data Structure Graph overview.
byDoug Needham
 
Social network analysis course 2010 - 2011
byguillaume ereteo
 
2009 Node XL Overview: Social Network Analysis in Excel 2007
byMarc Smith
 
Social Network Analysis
bySujoy Bag
 
Big social data analytics - social network analysis
byJari Jussila
 
02 Descriptive Statistics (2017)
byDuke Network Analysis Center
 
Social network analysis & Big Data - Telecommunications and more
byWael Elrifai
 
Exploring Social Media with NodeXL
byShalin Hai-Jew
 

Similar to LAK13 Tutorial Social Network Analysis 4 Learning Analytics

PPTX
CIC Networked Learning Practices Workshop - Caroline Haythornthwaite
byConnected Intelligence Centre, University of Technology, Sydney
 
PPTX
2010-November-8-NIA - Smart Society and Civic Culture - Marc Smith
byMarc Smith
 
PPTX
LSS'11: Charting Collections Of Connections In Social Media
byLocal Social Summit
 
PDF
socialnetworkanalysis-100225055227-phpapp02.pdf
byBalasundaramSr
 
PPTX
20111103 con tech2011-marc smith
byMarc Smith
 
PDF
Marc Smith - Charting Collections of Connections in Social Media: Creating Ma...
bySaratoga
 
PPTX
Acen presentation
byPaul Sijpkes
 
PDF
Social Network Analysis
byMesay Sata
 
PPTX
20120301 strata-marc smith-mapping social media networks with no coding using...
byMarc Smith
 
PDF
Socialnetworkanalysis 100225055227-phpapp02
byAdil Alpkoçak
 
PDF
The Mathematics of Social Network Analysis: Metrics for Academic Social Networks
byEditor IJCATR
 
PDF
Social Network Analysis [1994]
bysub-alkhalissi
 
PPTX
Learning with me Mate: Analytics of Social Networks in Higher Education
byDragan Gasevic
 
PDF
Social listening: how to do it and how to use (SNA Perspective)
byToronto Metropolitan University
 
PPTX
Visualizing Community through Social Network Analysis
byStephanie Richter
 
PPTX
20110128 connected action-node xl-sea of connections
byMarc Smith
 
PDF
Simple SNA.pdf
byBalasundaramSr
 
PPTX
AI Class Topic 5: Social Network Graph
byValue Amplify Consulting
 
PPTX
20111123 mwa2011-marc smith
byMarc Smith
 
PPTX
To understand importance of the the social networks insights and research dir...
byManonmani40
 
CIC Networked Learning Practices Workshop - Caroline Haythornthwaite
byConnected Intelligence Centre, University of Technology, Sydney
 
2010-November-8-NIA - Smart Society and Civic Culture - Marc Smith
byMarc Smith
 
LSS'11: Charting Collections Of Connections In Social Media
byLocal Social Summit
 
socialnetworkanalysis-100225055227-phpapp02.pdf
byBalasundaramSr
 
20111103 con tech2011-marc smith
byMarc Smith
 
Marc Smith - Charting Collections of Connections in Social Media: Creating Ma...
bySaratoga
 
Acen presentation
byPaul Sijpkes
 
Social Network Analysis
byMesay Sata
 
20120301 strata-marc smith-mapping social media networks with no coding using...
byMarc Smith
 
Socialnetworkanalysis 100225055227-phpapp02
byAdil Alpkoçak
 
The Mathematics of Social Network Analysis: Metrics for Academic Social Networks
byEditor IJCATR
 
Social Network Analysis [1994]
bysub-alkhalissi
 
Learning with me Mate: Analytics of Social Networks in Higher Education
byDragan Gasevic
 
Social listening: how to do it and how to use (SNA Perspective)
byToronto Metropolitan University
 
Visualizing Community through Social Network Analysis
byStephanie Richter
 
20110128 connected action-node xl-sea of connections
byMarc Smith
 
Simple SNA.pdf
byBalasundaramSr
 
AI Class Topic 5: Social Network Graph
byValue Amplify Consulting
 
20111123 mwa2011-marc smith
byMarc Smith
 
To understand importance of the the social networks insights and research dir...
byManonmani40
 

Recently uploaded

PPTX
28 January 2026 Rebecca Frankum Are high-stakes exams and assessments still r...
byEduSkills OECD
 
PPTX
HABIT. Cognitive process. I Semester Shilpa Hotakar pptx
bySHILPA HOTAKAR
 
PPTX
Powerpoint for testing in embed test with Sway
byjeanpierrefort3
 
PPTX
Reimagining Academic Library Services through Artificial Intelligence: A Case...
byDon Bosco College, Itanagar
 
PPTX
Poster Based Ethical Reflection - Dharma and Values Poster.pptx
byRajshreeBeneymadoo
 
PPTX
COMMUNICATION ITS PROCESS ELEMENTS & BARRIER .pptx
byPoojaSen20
 
PPTX
Appreciations - Jan 26 01.pptxkjkjkkjkjkjkj
bypreetheshparmar
 
PPTX
Mohan - "A man of silence and authority"
bynidhibachauhan46
 
PPTX
MENTAL STATUS EXAMINATION Part-1.Shilpa hotakar.pptx
bySHILPA HOTAKAR
 
PPTX
Unit 3- Culture.pptx....................
byAkanksha Kotangale
 
PPTX
TLE 8 W1 Q4 D2.pptx COMMON FLOOR PLAN SYMBOLS PLUMBING SYMBOLS
byraquelanaaltres1
 
PPTX
Drug Distribution in Pharmacology: Mechanisms, Barriers, Factors & Volume of ...
byamrin3379
 
PPTX
Central Line Associated Bloodstream Infection
bynabinabhaila40
 
PPT
West Hatch High School - GCSE History Option
byWestHatch
 
PPTX
YSPH VMOC Special Report - Measles - The Americas 1-25-2026
byYale School of Public Health - The Virtual Medical Operations Center (VMOC)
 
PDF
Risks and opportunities of artificial intelligence in education: A critical view
byYannis
 
PPTX
West Hatch High School - GCSE Art Presentation
byWestHatch
 
PPTX
Toba Tek Singh - Visualising Partition through Manto's Lens
bymiraljoshi48
 
PDF
Bishan_Singh_Presentation - Toba tek Singh
bygopalsinhchauhan9313
 
PPTX
Metabolism ( BIOCHEMISTRY & CLINICAL PATHOLOGY )
byBushraDeshpande
 
28 January 2026 Rebecca Frankum Are high-stakes exams and assessments still r...
byEduSkills OECD
 
HABIT. Cognitive process. I Semester Shilpa Hotakar pptx
bySHILPA HOTAKAR
 
Powerpoint for testing in embed test with Sway
byjeanpierrefort3
 
Reimagining Academic Library Services through Artificial Intelligence: A Case...
byDon Bosco College, Itanagar
 
Poster Based Ethical Reflection - Dharma and Values Poster.pptx
byRajshreeBeneymadoo
 
COMMUNICATION ITS PROCESS ELEMENTS & BARRIER .pptx
byPoojaSen20
 
Appreciations - Jan 26 01.pptxkjkjkkjkjkjkj
bypreetheshparmar
 
Mohan - "A man of silence and authority"
bynidhibachauhan46
 
MENTAL STATUS EXAMINATION Part-1.Shilpa hotakar.pptx
bySHILPA HOTAKAR
 
Unit 3- Culture.pptx....................
byAkanksha Kotangale
 
TLE 8 W1 Q4 D2.pptx COMMON FLOOR PLAN SYMBOLS PLUMBING SYMBOLS
byraquelanaaltres1
 
Drug Distribution in Pharmacology: Mechanisms, Barriers, Factors & Volume of ...
byamrin3379
 
Central Line Associated Bloodstream Infection
bynabinabhaila40
 
West Hatch High School - GCSE History Option
byWestHatch
 
YSPH VMOC Special Report - Measles - The Americas 1-25-2026
byYale School of Public Health - The Virtual Medical Operations Center (VMOC)
 
Risks and opportunities of artificial intelligence in education: A critical view
byYannis
 
West Hatch High School - GCSE Art Presentation
byWestHatch
 
Toba Tek Singh - Visualising Partition through Manto's Lens
bymiraljoshi48
 
Bishan_Singh_Presentation - Toba tek Singh
bygopalsinhchauhan9313
 
Metabolism ( BIOCHEMISTRY & CLINICAL PATHOLOGY )
byBushraDeshpande
 

LAK13 Tutorial Social Network Analysis 4 Learning Analytics

  • 1.
    Computational  Methods   and Tools  for  Social   Network  Analysis  of   Networked  Learning   Communities Tutorial at LAK 2013, 9/4/2013 Andreas Harrer, Tilman Göhnert, Alejandra Martínez-Monés & Christophe Reffay
  • 2.
    Agenda 13.30 Introduction ofpresenters and participants 13.45 Use Cases of SNA4LA 14.15 SNA Basics 15.15 Description of the practical workbench 15.30 COFFEE BREAK 16.00 Hands-on experiences using the workbench 17.30 End of the tutorial 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 2
  • 3.
    Introduction  of  presenters  &  participants 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 3
  • 4.
    Tutorial  Presenters •  AndreasHarrer •  Tillman Göhnert •  Alejandra Martínez-Monés •  Christophe Reffay 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 4
  • 5.
    Use  Cases  of SNA  for  LA 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 5
  • 6.
    Identifying  Participatory   Roles in  CSCL  scenarios Marcos García, J.A.,  Martínez Monés, A.,  Dimitriadis, Y.,  Anguita Martínez, R. A role-based approach for the support of collaborative learning activities e-Service Journal. 6(1):40-58, Diciembre 2007 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 6
  • 7.
    Participatory  roles •  Goal:Identifying roles based on their position within a network of relationships o  Description of expected roles, based on centrality indexes o  Identify the emergence of those roles in an experience o  Provide them with information adapted to their needs •  Approach: o  Description of roles based on “fuzzy” combinatios of SNA indexes 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 7
  • 8.
    Participatory  roles    (Distance  forum,  CSCL  2009) Isolated Non-participative
  • 9.
    Role: Dynamizer student Indicators OutdegreeCDo(i) Description Number of links initiated by this actor. V a l u e s / Interpretation A high value, indicates a high participation of the actor R e l e v a n c e rank First Outdegree sessions Description Specifies the relation between participation and number of sessions V a l u e s / Interpretation A high value indicates a high participation of the actor in the overall activity R e l e v a n c e rank Second Indegree CDi(i) Description Number of links terminating by this actor V a l u e s / Interpretation A medium value indicates a medium relevance R e l e v a n c e rank Third. Participatory  roles   Dynamizer  student 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 9
  • 10.
    Student  dynamizer    (Distance  forum,  CSCL  2009) Animator CDo(B20) = 16 CDo-sessions (B20) = 30,8% CDi (B20) = 4 (17th value) solated Non-participative
  • 11.
    Student  dynamizer    (Web-­‐‑based  document  sharing) 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 11 aalobel abalarr aordboa arodull cfergon cgeiveg cgonzrol cjimcab emonveg emunsei epadgon esasbaz estibaliz ggj ibalala ilizmar imunado jjimrio jorge lcaravi lconase lhergar Lmunbla marnmar Mcamalo mferrub mlauroth mmaygom mmiggut ncalgua Noelia papajim plagvel ppersan profe rapaduq rfueote rgorvil rmarcol rpermar Rumbram scilram scunfer sfermar smarmor vdiefer Vmaybar Animator
  • 12.
    Cohesion  in  subgroups  Reffay, C. and Chanier, T., (2003) How social network analysis can help to measure cohesion in collaborative distance learning, Proc of CSCL, 2003 Reffay, C., Teplovs, C., & Blondel, F.-M. (2011). Productive re- use of CSCL data and analytic tools to provide a new perspective on group cohesion. Proc of CSCL 2011. 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 12
  • 13.
    Cohesion •  Simugline dataset o  4 online groups working on an French as foreign language simulation o  Each group had an instructor and a •  Data o  Discussion forums that are local to each of the 4 groups •  Network o  The relation between “a” and “b” represents messages sent by “a” and opened by “b” plus messages posted by “b” and opened by “a” •  Indexes o  Cliques at level “c”: subgroup in which the ties between all pairs of agents have values c or greater (i.e., have exchanged c or more messages). o  “c” can be a value announced by the teacher as the desirable level of interaction 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 13
  • 14.
    Comparing groups with(level 10) cliques Aquitania Gallia Lugdunensis Gallia Narbonensis 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 14
  • 15.
    Hierarchical Clusters GALLIA G GG G G G G G G G l l l n l G l n l l l 1 Level 3 2 1 1 t 4 2 6 5 9 0 ----- - - - - - - - - - - - 167 . . . XXX . . . . . . 108 . . . XXXXX . . . . . 83 . . XXXXXXX . . . . . 64 . . XXXXXXXXX . . . . 52 . XXXXXXXXXXX . . . . 42 XXXXXXXXXXXXX . . . . 29 XXXXXXXXXXXXXXX . . . 9 XXXXXXXXXXXXXXX XXXXX 5 XXXXXXXXXXXXXXXXXXXXX 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 15
  • 16.
    PaNern  (Star)  => Intensity? Aquitania Lugdunensis Narbonensis GalliaIntensity=192 Intensity=12 Intensity=72 Intensity=111 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 16
  • 17.
    The  “fourth”  man Malzahn,N., Harrer, A., & Zeini, S. (2007). The Fourth Man - Supporting self-organizing group formation in learning communities. In Proc. of CSCL 2007 (pp. 547–550). 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 17
  • 18.
    18 Person-­‐‑ Topic-­‐‑ Network   from  Forum:  group   searches  for   the  „fourth   man“ 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
  • 19.
    19 Network   using   semantic  relations 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
  • 20.
    Blockmodeling Harrer, A. &Schmidt, A. (to appear 2013). Blockmodeling and role analysis in multi-relational networks. Social Networks and Mining. Springer. 2013 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 20
  • 21.
    21 Complex  networks  – dissolving  the  Death  Star 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
  • 22.
    22 Complex  networks  – dissolving  the  Death  Star 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
  • 23.
    23 Complex  networks  – dissolving  the  Death  Star 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
  • 24.
    A  Blockmodel  of this  network  –   positions  and  reduced  matrix 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 24
  • 25.
    SNA  basics 9/04/13 Computational Methodsand Tools for Social Network Analysis of Networked Learning Communities 25
  • 26.
    SNA  basics •  Whatis a Social Network? •  Types of networks and network transformations •  Useful definitions and measures on graphs •  Grouping concepts 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 26
  • 27.
    What  is  a social  network? •  A set of nodes (actors) o  Persons o  Groups o  Organizations o  Objects o  … •  A set of relationships o  Is a friend of o  Is neighbour of o  Provides goods to … o  Has sent a message to … o  Etc. 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 27
  • 28.
    What  is  a social  network? •  Complexity may increase. •  Analysis cannot be done by hand 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 28
  • 29.
    Ego-­‐‑net  :  The network  of   ego •  Ego: the selected node •  Alters (neighbours): distance (Ego,Alter) ≤ 1 o  Ties between ego and alter o  Ties between alters Whole network Ego-net (x34)Ego-net (x38) 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 29
  • 30.
    Types  of  Social Networks   According  to… •  Number of sets of actors o  One-mode : one set of actors o  Two-mode : (Bi-partite, affiliation networks) two sets of actors •  Relationships o  Directed or undirected o  Valued or un-valued (1/0) •  How are they built o  Complete networks o  Ego-networks 9/04/13Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 3030
  • 31.
    One-­‐‑mode  or  two-­‐‑mode  networks All nodes are of the same type •  Administrators •  Societies Two-modeOne-mode 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 31 Nodes belong to two sets •  Students
  • 32.
    Directed  vs  Undirected  graphs •  Directed Undirected Edges  are  oriented Edges  are  not  oriented 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 32
  • 33.
    Weighted  (valued)  vs  Unvalued  graphs •  Weighted/Valued •  Unvalued Edges  have  values Edges  have  no  value 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 33
  • 34.
    Conclusion:  8  possible  network  types One-mode (One node type) Two-mode (Two node types) • One-Mode • Directed • Valued • One-Mode • Undirected • Valued • One-Mode • Directed • Unvalued • One-Mode • Undirected • Unvalued • Two-Mode • Directed • Valued • Two-Mode • Undirected • Valued • Two-Mode • Directed • Unvalued • Two-Mode • Undirected • Unvalued 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 34
  • 35.
    Network  types   transformation allowed Two-­‐‑Mode One-­‐‑Mode Directed Undirected Valued Unvalued More  information Less  Information Selection strategy Not reversible! 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 35
  • 36.
    Two-­‐‑Mode One-­‐‑Mode 2 2 1 1 1 1 Do bluenodes share any orange resource? => Unvalued How many orange resource do blue nodes share ? => Valued Strategy: Decide what sharing resource represent for relationships between (blue) nodes. 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 36
  • 37.
    Directed Undirected Are nodesconnected (one tie is enough)? Are nodes connected with reciprocal edges? Strategy: Decide if you have/not edges in both directions. 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 37
  • 38.
    Valued Unvalued Threshold=5 Strategy: Onlyties with value>=Threshold are considered 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 38
  • 39.
    Useful  measures  of social   networks •  Density •  Degree, In-degree, Out-degree •  Path, Geodesic distance, Diameter •  Centrality indexes (for nodes) o  Degree centrality o  Betweenness centrality, o  Closeness centrality 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 39
  • 40.
    Eff.=0 Poss.=10 d=0 Eff.=2 Poss.=10 d=0.2 Eff.=4 Poss.=10 d=0.4 Eff.=8 Poss.=10 d=0.8 Eff.=10 Poss.=10 d=1 Density  (of  edges) for  an   undirected  graph edgespossiblenb edgeseffectivenb ddensity = 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 40
  • 41.
    Density  (of  edges) for  a   directed  graph Eff.=0 Poss.=20 d=0 Eff.=4 Poss.=20 d=0.2 Eff.=8 Poss.=20 d=0.4 Eff.=16 Poss.=20 d=0.8 Eff.=20 Poss.=20 d=1 Reciprocal edges count twice (twice more possible edges) 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 41
  • 42.
    1 4 2 6 58 3 7 Net A 1 2 4 5 6 8 3 7 Net B The  structure  as  a  constraint   Do nodes “4” and “5” have the same role in nets A and B? Density: DA=9/28=0,321 Density: DB=9/28=0,321 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 42
  • 43.
    Centrality •  Who iscentral in this network? 439/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities
  • 44.
    Degree  in  an undirected   graph •  For a node, Degree = number of edges 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 44
  • 45.
    In-­‐‑  &  Out-­‐‑ degree  in  an   directed  graph In-­‐‑degree    =  number  of  edges  coming  into  the  node Out-­‐‑degree    =  number  of  edges  coming  out  of  the  node 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 45
  • 46.
    Path  :  sequence of  edges   connecting  2  nodes A H B C G D E F I J From A->E : 2 possible paths: • (A B C E) or • (A B D E) Example in a directed graph 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 46
  • 47.
    Path:  example  in an   undirected  graph A H B C G D E F I J From A->E : 2 possible paths: • (D E) or • (D B C E) Geodesic Distance: Length of the shortest path d(D,E) = 1 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 47
  • 48.
    Diameter  of  the graph •  Diameter = longest distance in the graph = maximal distance between any pair of nodes What is the diameter of this graph? D = 7 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 48
  • 49.
    Betweenness  centrality   • Number of shortest paths passing through the node Directed graph Undirected graph 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 49
  • 50.
    Closeness  centrality   Scoringthe closeness of one node to all others Undirected graph Directed graph 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 50
  • 51.
    The Moreno’s experiments (1943) Pupilsrelation in the classroom: •  Pupils of various age range •  Gender study « If you could choose freely, which are the (2) kids you would like to have as direct neighbour? » Main results: At <age> => pupils tend to <?> • 6-8 years old => mix • 8-13 years old => separate • 13-15 years old => mix • 15-17 years old => separate 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 51
  • 52.
    Moreno’s  network •  Whois central in this network? 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 52
  • 53.
    Components   Removing bridges     (cut-­‐‑points)… 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 53
  • 54.
    …This  results  in breaking   the  component   9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 54
  • 55.
    Grouping  concepts  – an   overview Groups can be determined according to different criteria •  Reachability and Distance – group member is connected via short ways to all other group members o  Direct links – Clique as complete subgraph o  Relaxing the distance – n-Clique requires all nodes being connected via short path (lesser and equal than n) •  Node degree – group member should be connected to many group members o  Leaving out a small number of group members: k-Plex o  Having at least k group members as direct neighbours – k-Core •  Contrasting “ingroup” and “outgroup” – density inside is much higher than outside o  Alliance: only links to ingroup, no links to outside 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 55
  • 56.
    Grouping  concepts  – an   overview •  Group concepts fall in two categories: o  Overlapping concepts •  e.g. Cliques o  Disjunct concepts •  e.g. k-cyclic blocks •  Depending on the type of analysis both categories have their merits o  Disjunct concepts allow clear-cut assignment to one group o  Overlapping concepts allow analysis of transfer ideas, e.g. Clique percolation 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 56
  • 57.
    Cliques  or  K-­‐‑cliques  Clique: maximum subset where all nodes are connected K-clique: Clique with K members How  many     cliques? • One 5-clique • One 4-clique • One 3-clique • Three 2-cliques => 6 cliques Which  are…  ? 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 57
  • 58.
    K-­‐‑cores 9/04/13 Computational Methods andTools for Social Network Analysis of Networked Learning Communities 58 Taken from: V. Batagelj, A. Mrvar / Social Networks 22 (2000) 173-186
  • 59.
    Clique  Percolation   Method • CPM allows overlapping communities •  Idea: a k-clique “percolates” through the graph •  Overlapping members can be “brokers” between groups 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 59 Taken from: Wikipedia
  • 60.
    Visualization  influences   Interpretation 9/04/13 ComputationalMethods and Tools for Social Network Analysis of Networked Learning Communities 60
  • 61.
    Practical  Workbench    Presentation 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 61
  • 62.
    Task  one:  Simuligne  Data  Preprocessing 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 62 Raw Data: A network with weighted, directed edges (Number of forum posts opened) Preprocessing: Symmetrisation of edge weights (by minimum, maximum, sum, or average)
  • 63.
    Task  one:  Simuligne • Choose the data set based on preprocessing o  Narbo_Max: Maximum of both directions o  Narbo_Mean: Average of both directions o  Narbo_Min: Minimum of both directions o  Narbo_Sum: Sum of both directions •  Think of the format transformation (UCINET -> SISOB) •  Focus on the appropriate intensity level of the relation •  Identify groups •  Choose an appropriate output representation 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 63
  • 64.
    Task  two:  Collaboration  over  Artifacts  (BSCW) 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 64 •  Two node types o  BSCW (document sharing) folders as artifacts (-..) •  One folder for general information •  Folders for individual case studies o  Pairs of students, each working mainly on a single case (x..) •  Edges weighted by access
  • 65.
    Task  two:  Collaboration  over  Artifacts  (BSCW) 9/04/13 Computational Methods and Tools for Social Network Analysis of Networked Learning Communities 65 •  Choose one of the data sets o  sp1_B_cli_cp_U.txt o  sp2_B_cli_cp_U.txt o  sp3_B_cli_cp_U.txt o  spf_B_cli_cp_U.txt •  Think of the format transformation (UCINET -> SISOB) •  Try to identify the general folder •  Try to identify the projects the pairs of students worked on •  Analyse the collaboration between the students (hint: Folding is also in the R-Analysis)