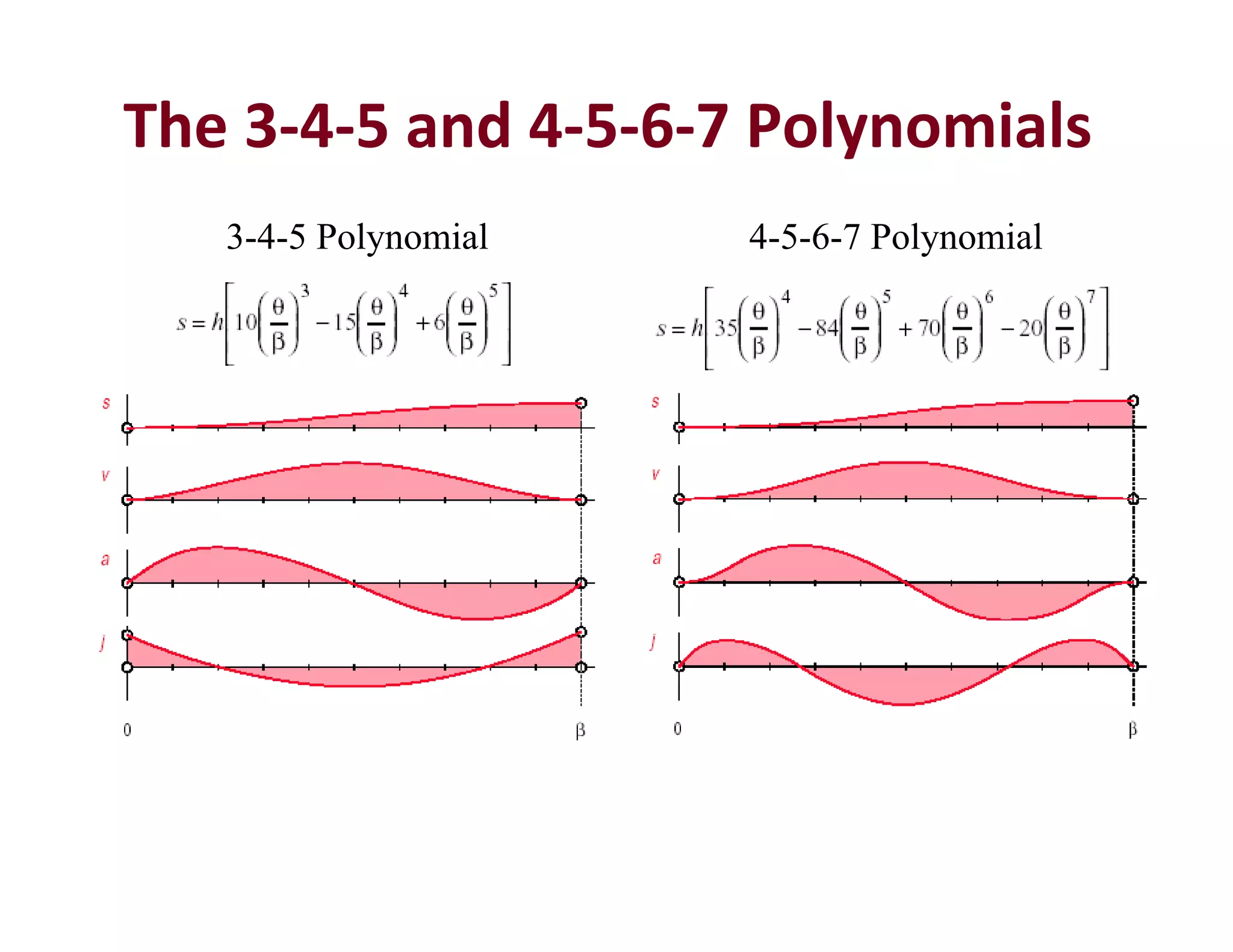
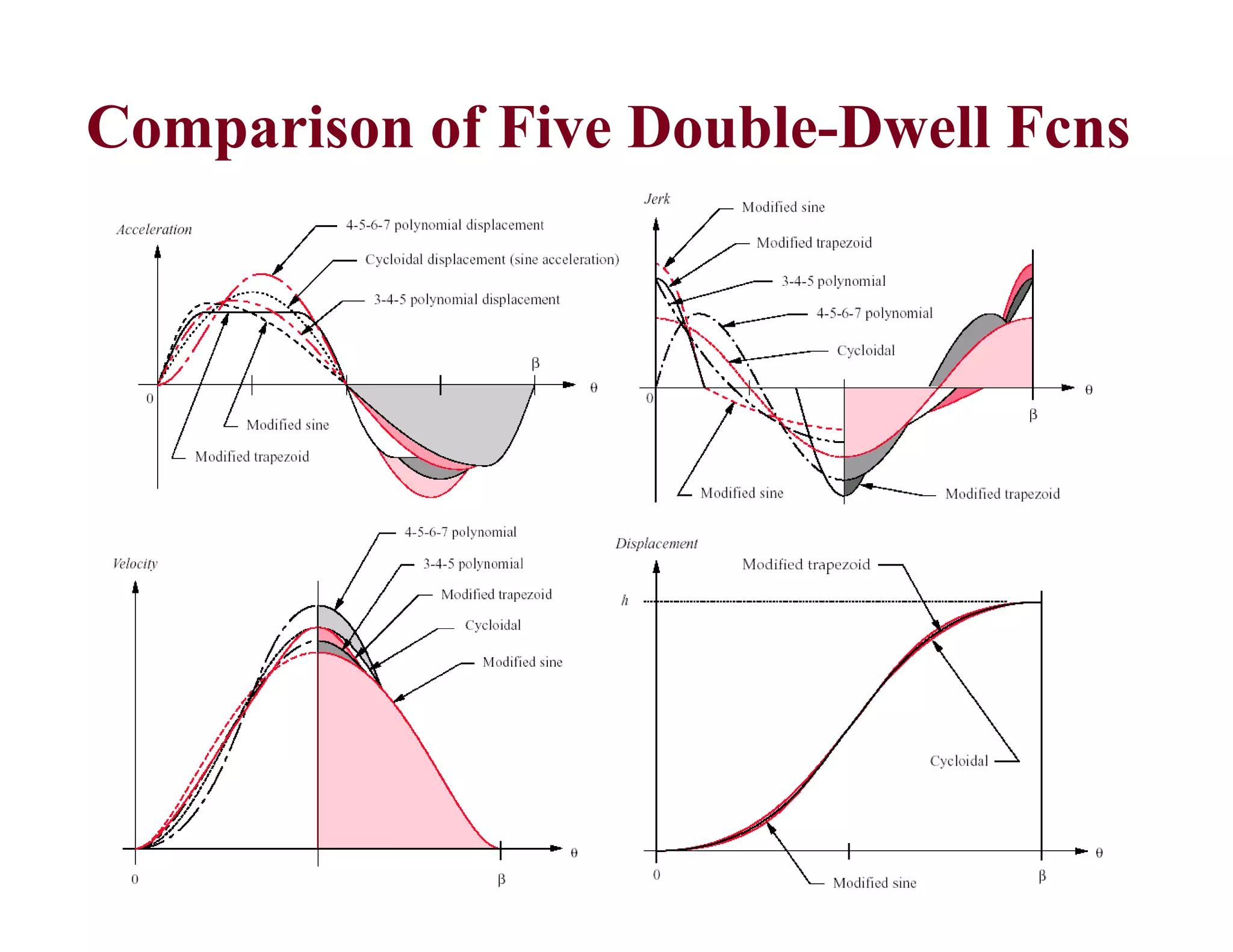
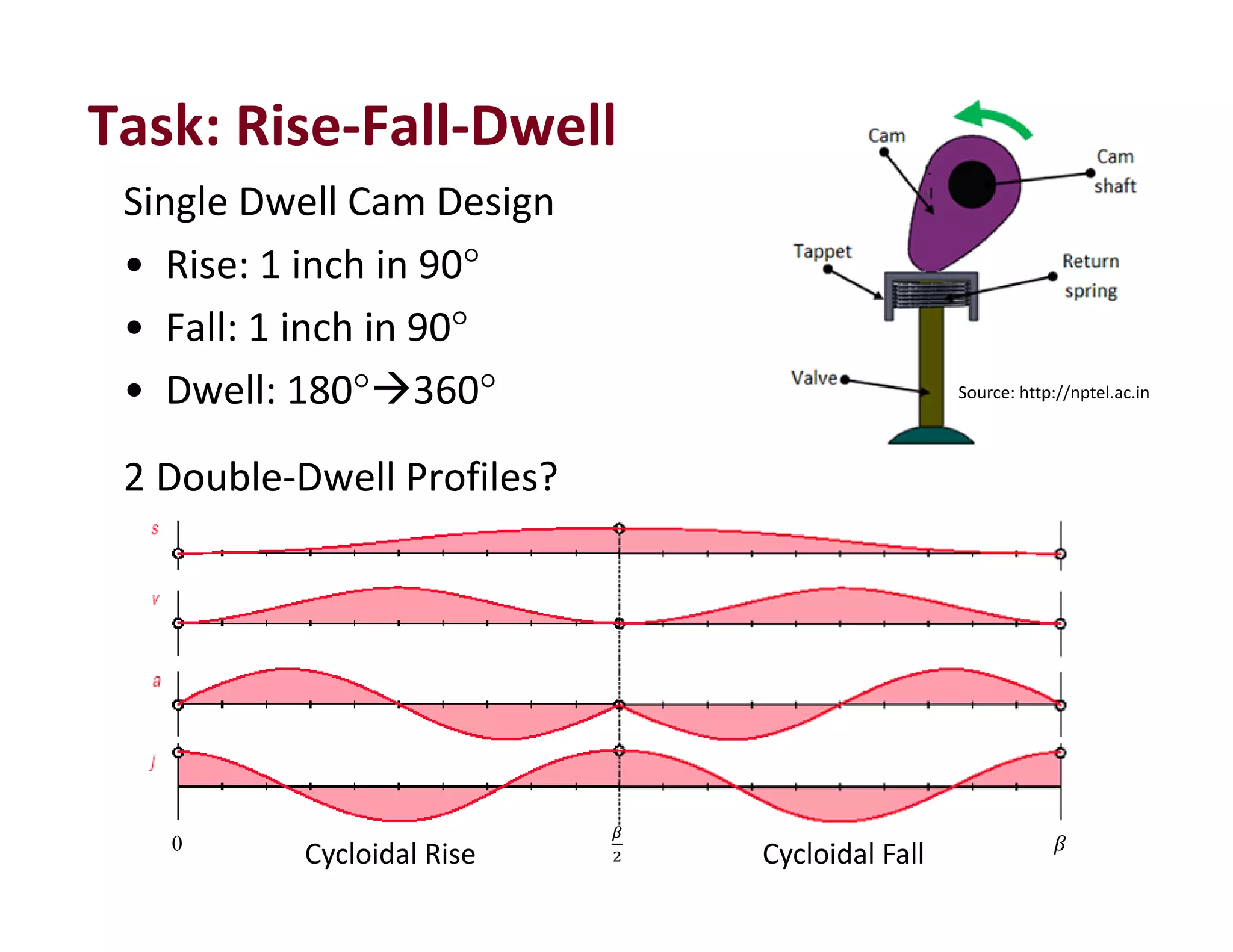
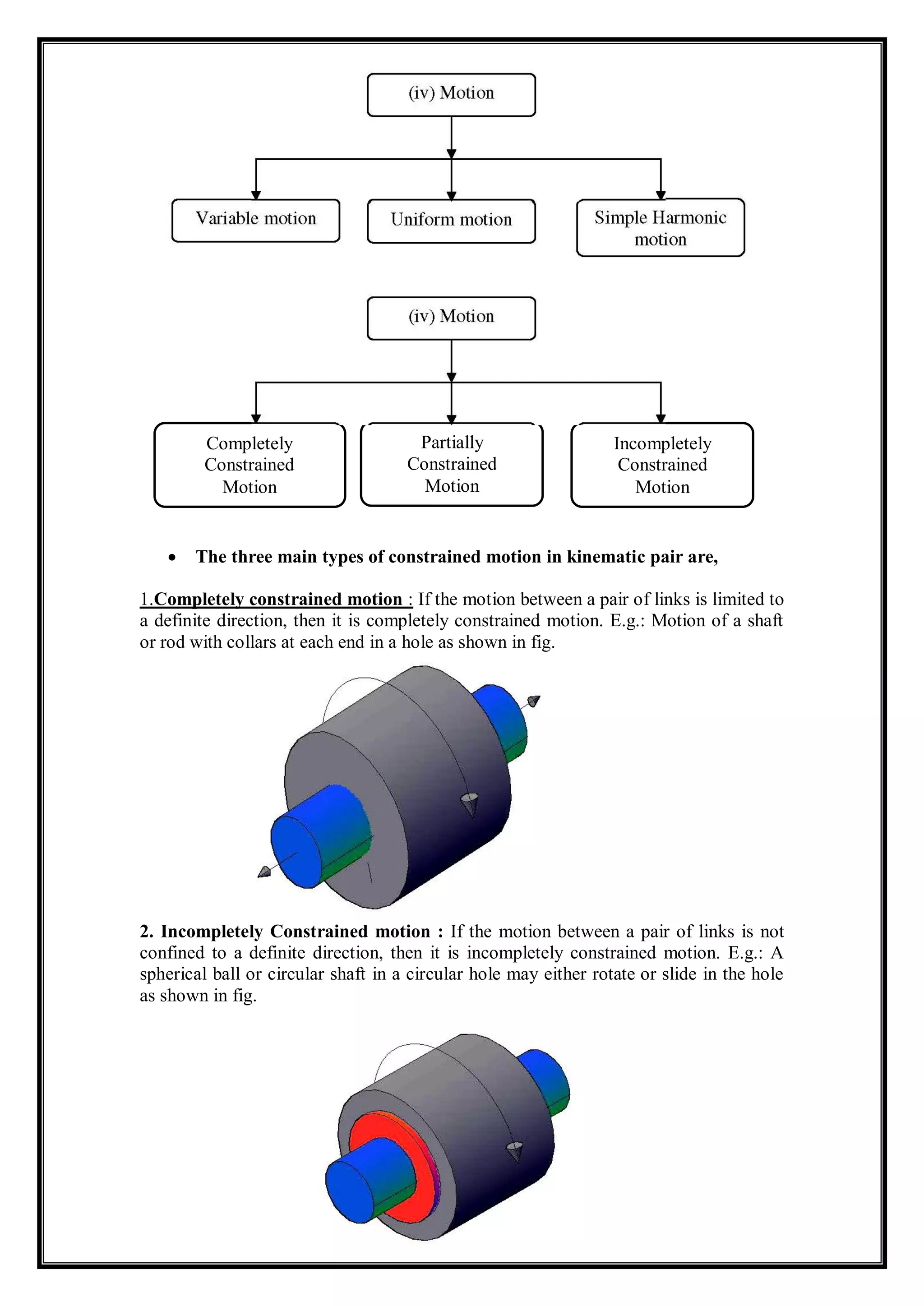
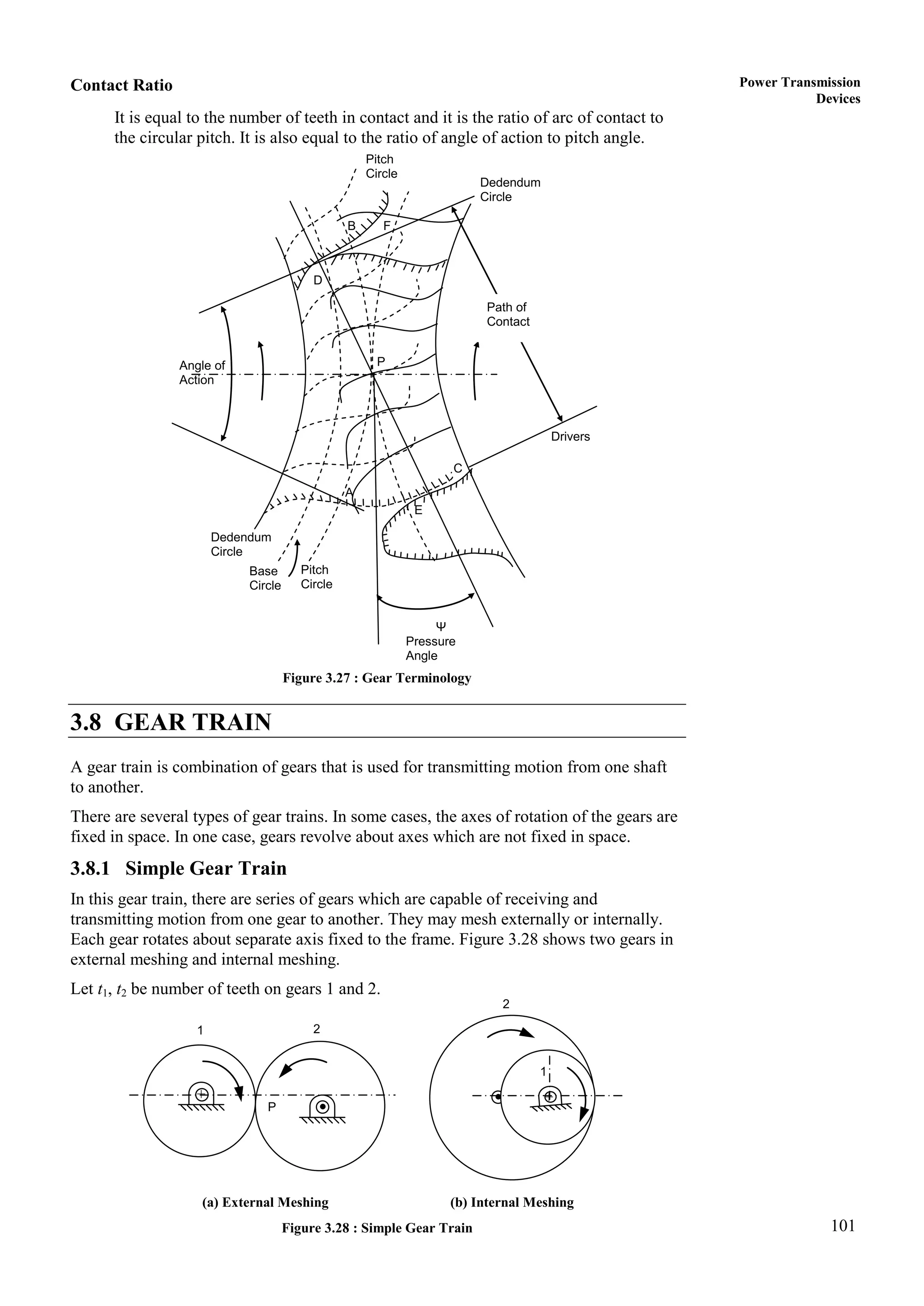
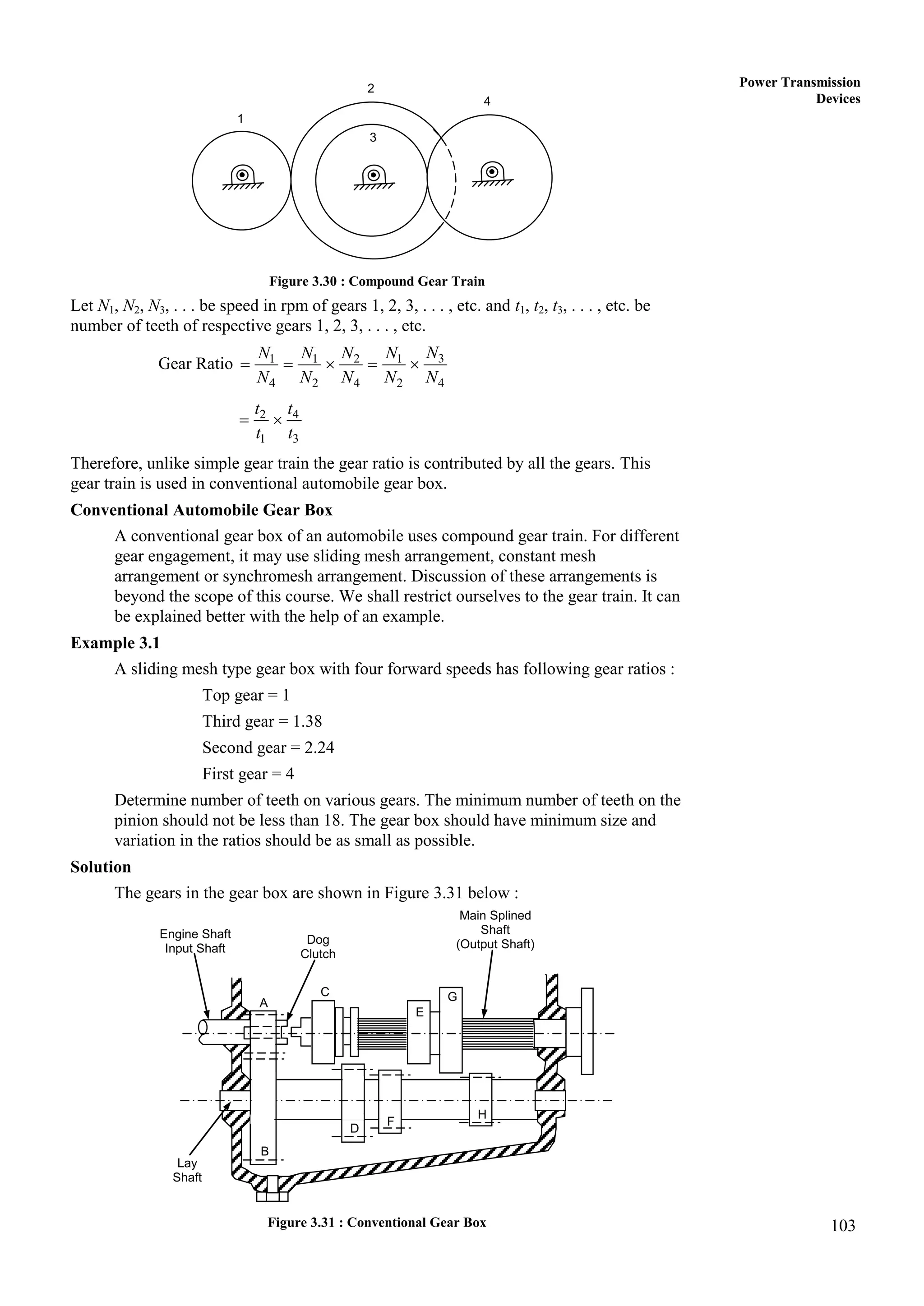
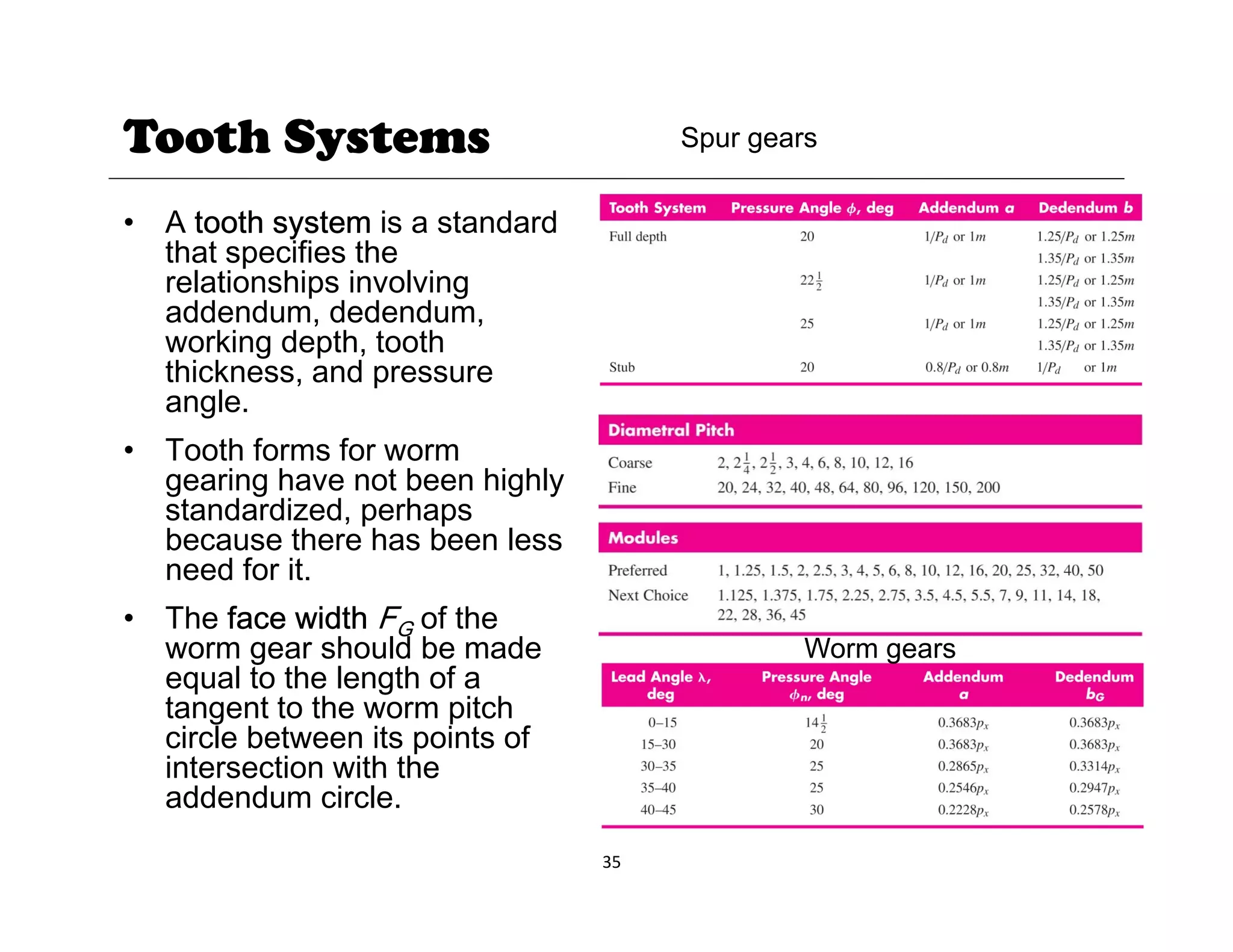
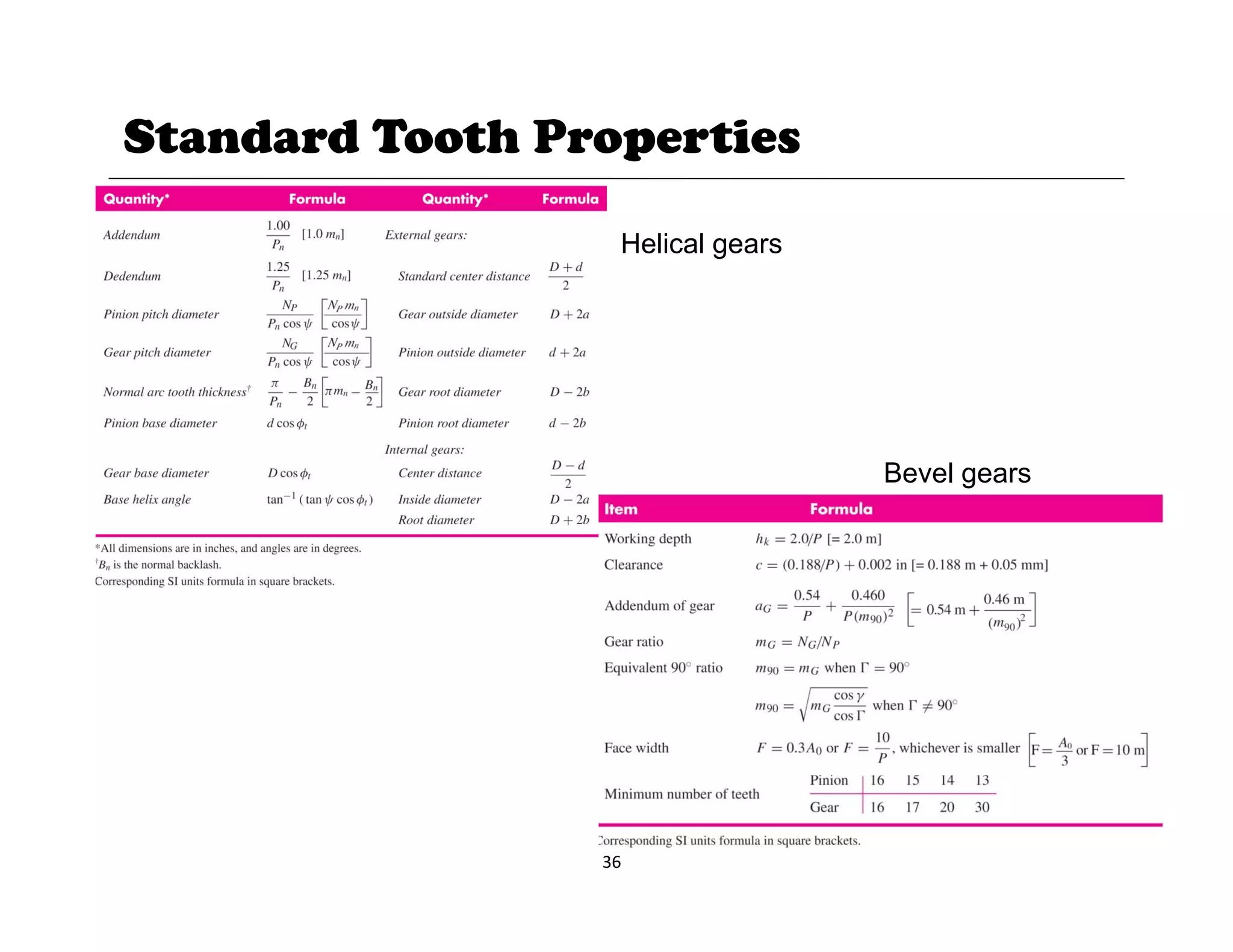
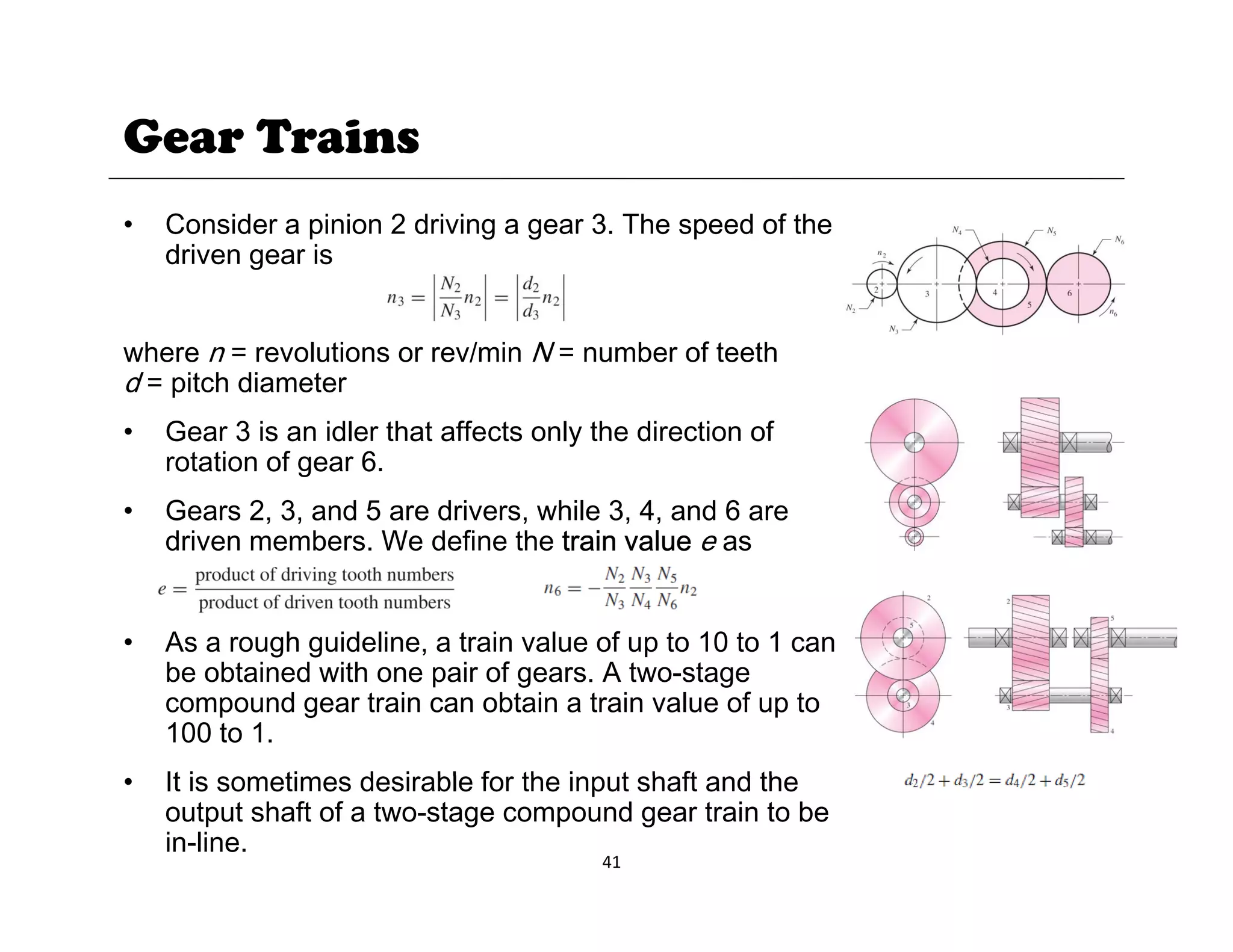
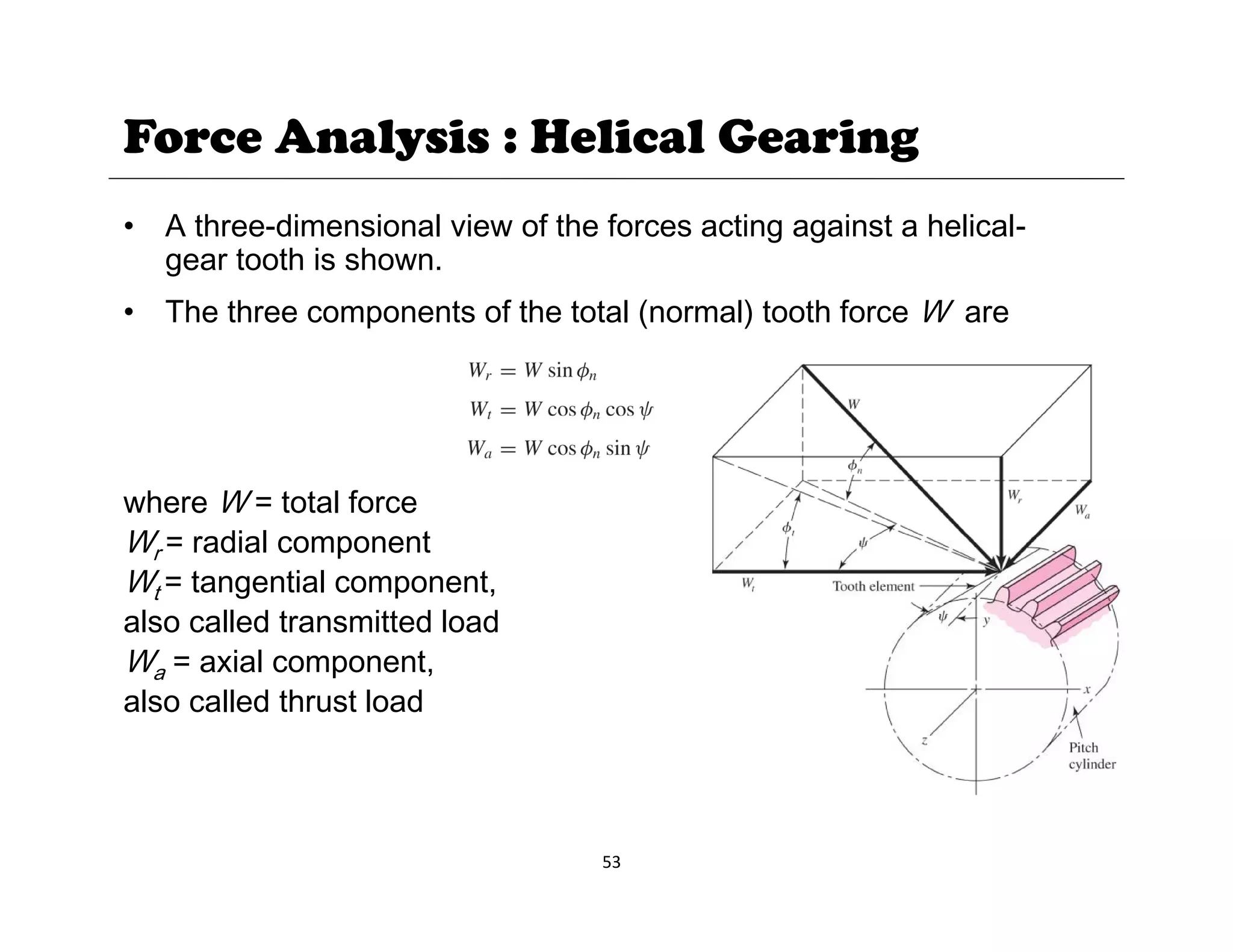
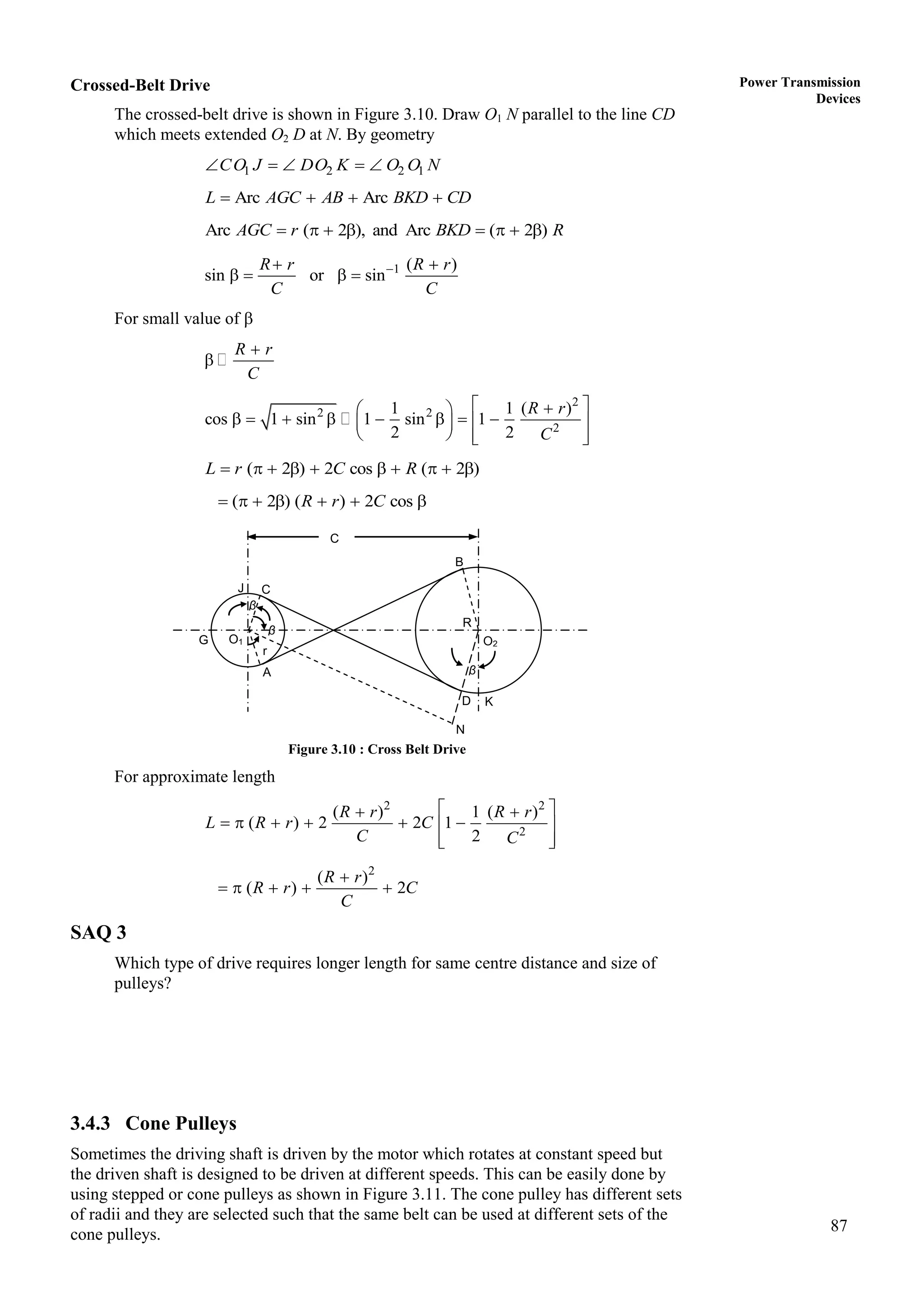
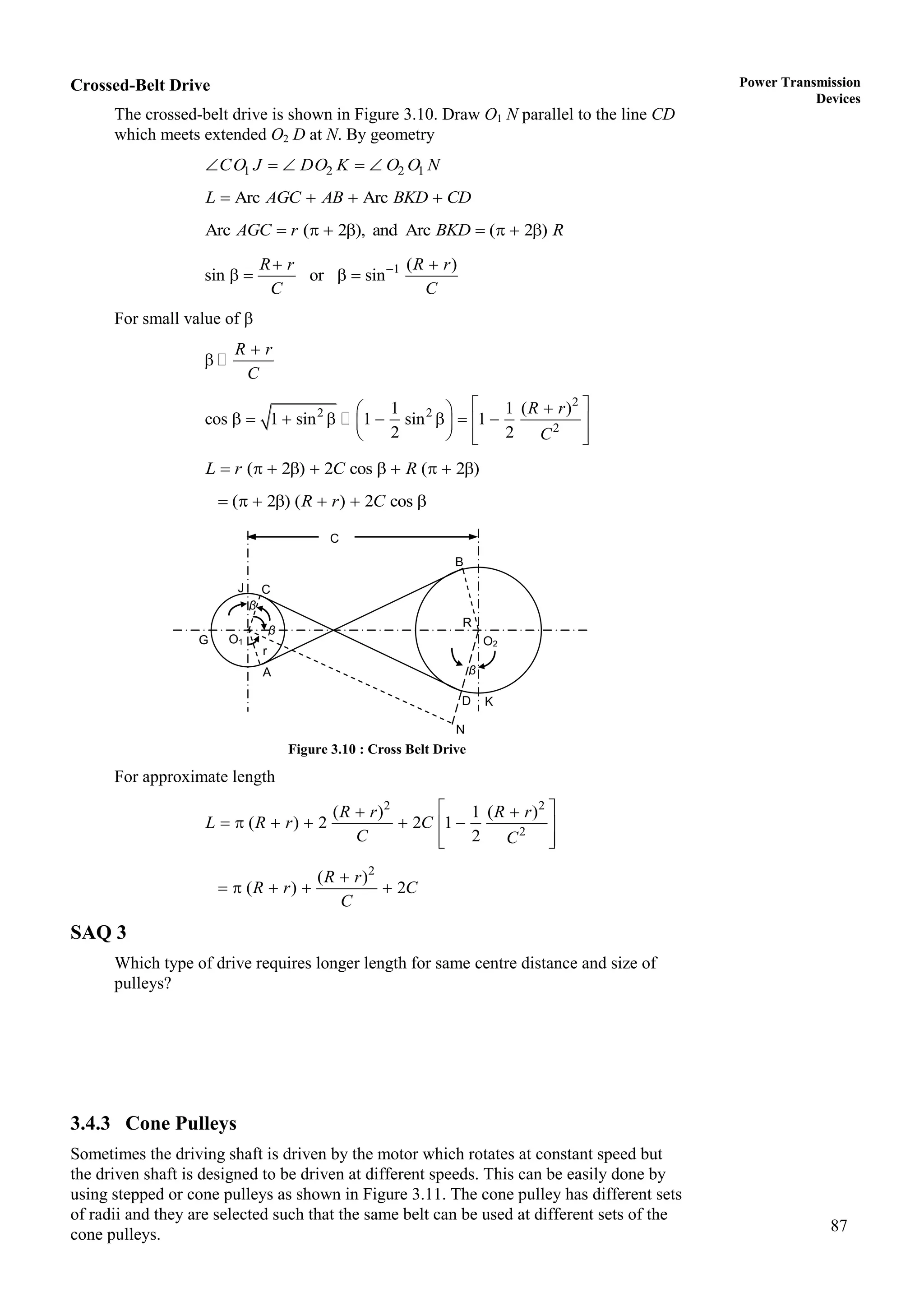
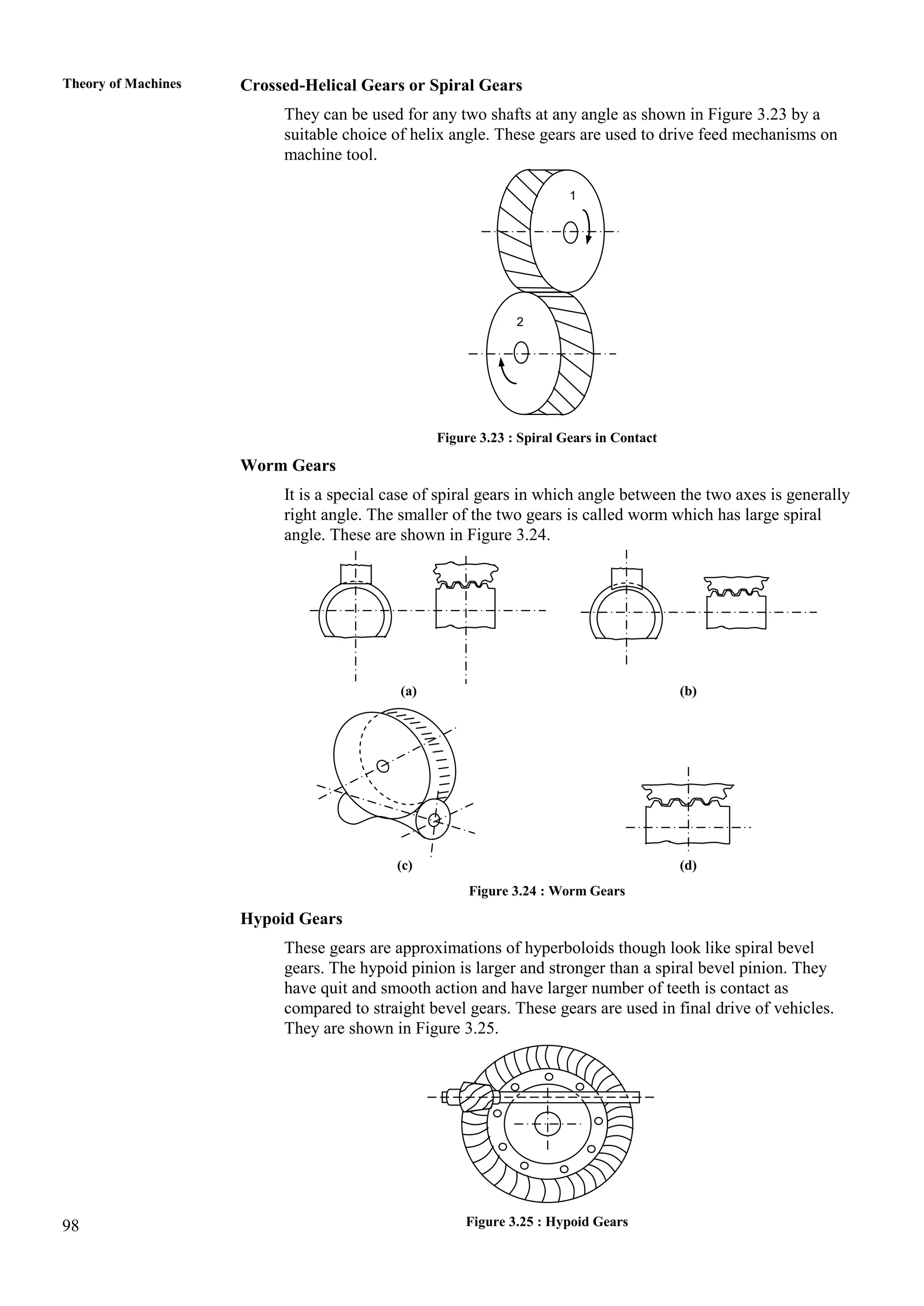
1. The document provides lecture notes on kinematics of machinery, covering topics such as mechanisms, kinematic pairs, mobility, and straight line motion mechanisms. 2. Key concepts discussed include degrees of freedom, links and joints, kinematic chains, mechanisms versus machines, and types of constrained motion. Common mechanisms like slider crank and four bar linkages are also introduced. 3. The objectives of the course are to understand basic kinematic principles, analyze various mechanisms for displacement, velocity and acceleration, and examine gears, gear trains, cams and other machine elements. The course covers analysis of mechanisms using methods like velocity and acceleration diagrams, instantaneous centers, and cam profiles.

1. LECTURE NOTES
ON
KINEMATICS OF MACHINERY
2018 – 2019
II B. Tech II Semester (17CA03404)
Mr. S.Praveen kumar
Assistant Professor
CHADALAWADA RAMANAMMA ENGINEERING COLLEGE
(AUTONOMOUS)
Chadalawada Nagar, Renigunta Road, Tirupati – 517 506
Department of Mechanical Engineering

2. KINEMATICS OF MACHINERY
II B.Tech IV Semester: ME
Course Code Category Hours / Week Credits Maximum Marks
17CA03404 Core
L T P C CIA SEE Total
2 2 - 3 30 70 100
Contact Classes: 34 Tutorial Classes: 34 Practical Classes: Nil Total Classes: 68
OBJECTIVES:
The course should enable the students to:
I. Understand the basic principles of kinematics and the related terminology of machines.
II. Discriminate mobility, enumerate links and joints in the mechanisms.
III. Formulate the concept of analysis of different mechanisms.
IV. Understand the working of various straight line mechanisms, gears, gear trains, steering gear mechanisms,
cams and a Hooke’s joint.
V. Analyze a mechanism for displacement, velocity and acceleration of links in a machine.
UNIT-I MECHANISMS & MACHINE Classes: 14
MECHANISMS AND MACHINES: Elements or Links – Classification – Rigid Link, flexible and fluid link.
Types of kinematic pairs – sliding, turning, rolling, screw and spherical pairs – lower and higher pairs – closed and
open pairs – constrained motion – completely, partially or successfully constrained and incompletely constrained.
Mechanisms and machines – classification of mechanisms and machines – kinematic chain – inversion of
mechanisms – inversions of quadric cycle chain – single and double slider crank chain.Mobility of mechanisms.
Straight Line Motion Mechanisms- Exact and approximate, copiers and generated types –Peaucellier, Hart and
Scott Russel – Grasshopper, Watt, Tchebicheff and Robert Mechanisms. Pantograph.
UNIT-II STEERING MECHANISMS & BELT, ROPE AND CHAIN DRIVES : Classes: 14
STEERING MECHANISMS: Conditions for correct steering – Davis Steering gear, Ackermanns steering gear.
Hooke’s Joint (Universal coupling) -Single and double Hooke’s joint –– applications – Simple problems.
Belt, Rope and Chain Drives : Introduction, Belt and rope drives, selection of belt drive- types of belt drives,
materials used for belts and ropes, velocity ratio of belt drives, slip of belt, creep of belt, tensions for flat belt drive,
angle of contact, centrifugal tension, maximum tension of belt, Chains- length, angular speed ratio, classification
of chains.
UNIT-III KINEMATICS Classes: 14
Velocity and Acceleration Diagrams: Velocity and acceleration – Motion of link in machine – Determination of
Velocity and acceleration – Graphical method – Application of relative velocity method – Slider crank mechanism,
four bar mechanism. Acceleration diagrams for simple mechanisms, Coriolis acceleration, determination of
Coriolis component of acceleration. Kleins construction. Analysis of slider crank mechanism for displacement,
velocity and acceleration of slider using analytical method
Instantaneous Centre Method: Instantaneous centre of rotation, Instantaneous centre for simple mechanisms, and
determination of angular veloties of points and links. centrode and axode – relative motion between two bodies –
Three centres in-line theorem.
UNIT-IV GEARS & GEAR TRAINS: Classes: 12
GEARS: Introduction to gears and types of gears(Spur, Helical, Bevel and worm gears) , friction wheels and– law
of gearing, condition for constant velocity ratio for transmission of motion, Forms of tooth- cycloidal and involute
profiles. Velocity of sliding – phenomena of interference – Methods to avoid interference. Condition for minimum
number of teeth to avoid interference, expressions for arc of contact and path of contact.
GEAR TRAINS: Introduction –Types of gear trains – Simple, compound, reverted and Epicyclic gear trains.
Train value – Methods of finding train value or velocity ratio – Tabular column method for Epicyclic gear trains.
Torque in epicyclic gear trains. Differential gear of an automobile.

3. Note: End Examination should be conducted in drawing hall.
UNIT-V CAMS & ANALYSIS OF MOTION OF FOLLOWERS: Classes: 14
CAMS: Definitions of cam and follower – uses – Types of followers and cams – Terminology. Types of follower
motion - Uniform velocity – Simple harmonic motion and uniform acceleration, Offset method for CAM profiles.
Maximum velocity and maximum acceleration during outward and return strokes. Drawing of cam profiles.
ANALYSIS OF MOTION OF FOLLOWERS: Tangent cam with roller follower – circular arc (Convex) cam
with flat faced and roller follower.
Text Books:
1. Joseph E. Shigley, “Theory of Machines and Mechanisms”, Oxford University Press, 4th
Edition, 2010.
2. S.S. Rattan, “Theory of Machines”, Tata McGraw Hill Education, 1st
Edition, 2009.
Reference Books:
1. Jagadish Lal, “Theory of Mechanisms and Machines”, Metropolitan Book Company, 1st
Edition, 1978.
2. Norton, “Kinematics and Dynamics of Machinery”, Tata McGraw Hill, 3rd
Edition, 2008.
3. Sadhu Singh, “Theory of Machines”, Pearson, 2nd
Edition, 2006.
4. J. S Rao, R. V Duggipati, “Mechanisms and Machine Theory”, New Age Publishers, 2nd
Edition, 2008.
5. R. K. Bansal, “Theory of Machines”, Lakshmi Publications, 1st
Edition, 2013.
6. Thomas Bevan, “Theory of Machines”, Pearson, 3rd
Edition, 2009.
Course Outcomes:
1. Identify different types of mechanisms and inversions of different kinematic chains.
2. Calculate the basic parameters for Hooke’s joint, steering mechanisms and belt drives.
3. Analyze velocity and acceleration at different point in a simple plane mechanism using relative velocity
method and instantaneous center method.
4. Calculate pitch, module, number of teeth, path of contact for meshing gears and train value for different gear
trains by using tabular column method.
5. Analyze displacement, velocity and acceleration of cam follower at different positions of cam with specified
contours by drawing displacement diagram and cam profile for different types of motions (SHM, UARM and
uniform velocity) of cam and follower.

4. Unit I BASICS OF MECHANISMS
 Introduction:
Definitions : Link or Element, Pairing of Elements with degrees of freedom,
Grubler’s criterion (without derivation), Kinematic chain, Mechanism, Mobility of
Mechanism, Inversions, Machine.
 Kinematic Chains and Inversions :
Kinematic chain with three lower pairs, Four bar chain, Single slider crank chain
and Double slider crank chain and
their inversions.
 Mechanisms:
i) Quick return motion mechanisms – Drag link mechanism, Whitworth
mechanism and Crank and slotted lever mechanism
ii) Straight line motion mechanisms – Peacelier’s mechanism and Robert’s
mechanism.
iii) Intermittent motion mechanisms – Geneva mechanism and Ratchet & Pawl
mechanism.
iv) Toggle mechanism, Pantograph, Hooke’s joint and Ackerman Steering gear
mechanism.
1. Terminology and Definitions-Degree of Freedom, Mobility
 Kinematics: The study of motion (position, velocity, acceleration). A major
goal of understanding kinematics is to develop the ability to design a system
that will satisfy specified motion requirements. This will be the emphasis of
this class.
 Kinetics: The effect of forces on moving bodies. Good kinematic design
should produce good kinetics.
 Mechanism: A system design to transmit motion. (low forces)
 Machine: A system designed to transmit motion and energy. (forces
involved)
 Basic Mechanisms: Includes geared systems, cam-follower systems and
linkages (rigid links connected by sliding or rotating joints). A mechanism
has multiple moving parts (for example, a simple hinged door does not qualify
as a mechanism).
 Examples of mechanisms: Tin snips, vise grips, car suspension, backhoe,
piston engine, folding chair, windshield wiper drive system, etc.
Key concepts:
 Degrees of freedom: The number of inputs required to completely control a
system. Examples: A simple rotating link. A two link system. A four-bar
linkage. A five-bar linkage.
 Types of motion: Mechanisms may produce motions that are pure rotation,
pure translation, or a combination of the two. We reduce the degrees of
freedom of a mechanism by restraining the ability of the mechanism to move
in translation (x-y directions for a 2D mechanism) or in rotation (about the z-
axis for a 2-D mechanism).

5.  Link: A rigid body with two or more nodes (joints) that are used to connect to
other rigid bodies. (WM examples: binary link, ternary link (3 joints),
quaternary link (4 joints))
 Joint: A connection between two links that allows motion between the links.
The motion allowed may be rotational (revolute joint), translational (sliding or
prismatic joint), or a combination of the two (roll-slide joint).
 Kinematic chain: An assembly of links and joints used to coordinate an
output motion with an input motion.
 Link or element:
A mechanism is made of a number of resistant bodies out of which some may have
motions relative to the others. A resistant body or a group of resistant bodies with
rigid connections preventing their relative movement is known as a link.

6. A link may also be defined as a member or a combination of members of a
mechanism, connecting other members and having motion relative to them, thus a
link may consist of one or more resistant bodies. A link is also known as Kinematic
link or an element.
Links can be classified into 1) Binary, 2) Ternary, 3) Quarternary, etc.
 Kinematic Pair:
A Kinematic Pair or simply a pair is a joint of two links having relative motion
between them.
Example:
In the above given Slider crank mechanism, link 2 rotates relative to link 1 and
constitutes a revolute or turning pair. Similarly, links 2, 3 and 3, 4 constitute turning
pairs. Link 4 (Slider) reciprocates relative to link 1 and its a sliding pair.
Types of Kinematic Pairs:
Kinematic pairs can be classified according to
i) Nature of contact.
ii) Nature of mechanical constraint.
iii) Nature of relative motion.
i) Kinematic pairs according to nature of contact :
a) Lower Pair: A pair of links having surface or area contact between the members is
known as a lower pair. The contact surfaces of the two links are similar.
Examples: Nut turning on a screw, shaft rotating in a bearing, all pairs of a slider-
crank mechanism, universal joint.
b) Higher Pair: When a pair has a point or line contact between the links, it is known
as a higher pair. The contact surfaces of the two links are dissimilar.
Examples: Wheel rolling on a surface cam and follower pair, tooth gears, ball and
roller bearings, etc.
ii) Kinematic pairs according to nature of mechanical constraint.
a) Closed pair: When the elements of a pair are held together mechanically, it is
known as a closed pair. The contact between the two can only be broken only by the
destruction of at least one of the members. All the lower pairs and some of the higher
pairs are closed pairs.

7. b) Unclosed pair: When two links of a pair are in contact either due to force of gravity
or some spring action, they constitute an unclosed pair. In this the links are not held
together mechanically. Ex.: Cam and follower pair.
iii) Kinematic pairs according to nature of relative motion.
a) Sliding pair: If two links have a sliding motion relative to each other, they form a
sliding pair. A rectangular rod in a rectangular hole in a prism is an example of a
sliding pair.
b) Turning Pair: When on link has a turning or revolving motion relative to the other,
they constitute a turning pair or revolving pair.
c) Rolling pair: When the links of a pair have a rolling motion relative to each other,
they form a rolling pair. A rolling wheel on a flat surface, ball ad roller bearings, etc.
are some of the examples for a Rolling pair.
d) Screw pair (Helical Pair): if two mating links have a turning as well as sliding
motion between them, they form a screw pair. This is achieved by cutting matching
threads on the two links.
The lead screw and the nut of a lathe is a screw Pair
e) Spherical pair: When one link in the form of a sphere turns inside a fixed link, it is
a spherical pair. The ball and socket joint is a spherical pair.
 Degrees of Freedom:
An unconstrained rigid body moving in space can describe the following independent
motions.
1. Translational Motions along any three mutually perpendicular axes x, y and z,
2. Rotational motions along these axes.
Thus a rigid body possesses six degrees of freedom. The connection of a link with
another imposes certain constraints on their relative motion. The number of restraints
can never be zero (joint is disconnected) or six (joint becomes solid).
Degrees of freedom of a pair is defined as the number of independent relative
motions, both translational and rotational, a pair can have.
Degrees of freedom = 6 – no. of restraints.
To find the number of degrees of freedom for a plane mechanism we have an equation
known as Grubler’s equation and is given by F = 3 ( n – 1 ) – 2 j1 – j2
F = Mobility or number of degrees of freedom
n = Number of links including frame.
j1 = Joints with single (one) degree of freedom.
J2 = Joints with two degrees of freedom.
If F > 0, results in a mechanism with ‘F’ degrees of freedom.
F = 0, results in a statically determinate structure.
F < 0, results in a statically indeterminate structure.
 Kinematic Chain:
A Kinematic chain is an assembly of links in which the relative motions of the links is
possible and the motion of each relative to the others is definite (fig. a, b, and c.)

8. In case, the motion of a link results in indefinite motions of other links, it is a non-
kinematic chain. However, some authors prefer to call all chains having relative
motions of the links as kinematic chains.
 Linkage, Mechanism and structure:
A linkage is obtained if one of the links of kinematic chain is fixed to the ground. If
motion of each link results in definite motion of the others, the linkage is known as
mechanism. If one of the links of a redundant chain is fixed, it is known as a structure.
To obtain constrained or definite motions of some of the links of a linkage, it is
necessary to know how many inputs are needed. In some mechanisms, only one input
is necessary that determines the motion of other links and are said to have one degree
of freedom. In other mechanisms, two inputs may be necessary to get a constrained
motion of the other links and are said to have two degrees of freedom and so on.
The degree of freedom of a structure is zero or less. A structure with negative degrees
of freedom is known as a Superstructure.
 Motion and its types:

9.  The three main types of constrained motion in kinematic pair are,
1.Completely constrained motion : If the motion between a pair of links is limited to
a definite direction, then it is completely constrained motion. E.g.: Motion of a shaft
or rod with collars at each end in a hole as shown in fig.
2. Incompletely Constrained motion : If the motion between a pair of links is not
confined to a definite direction, then it is incompletely constrained motion. E.g.: A
spherical ball or circular shaft in a circular hole may either rotate or slide in the hole
as shown in fig.
Completely
Constrained
Motion
Partially
Constrained
Motion
Incompletely
Constrained
Motion

10. 3. Successfully constrained motion or Partially constrained motion: If the motion
in a definite direction is not brought about by itself but by some other means, then it is
known as successfully constrained motion. E.g.: Foot step Bearing.
 Machine:
It is a combination of resistant bodies with successfully constrained motion which is
used to transmit or transform motion to do some useful work. E.g.: Lathe, Shaper,
Steam Engine, etc.
 Kinematic chain with three lower pairs
It is impossible to have a kinematic chain consisting of three turning pairs only. But it
is possible to have a chain which consists of three sliding pairs or which consists of a
turning, sliding and a screw pair.
The figure shows a kinematic chain with three sliding pairs. It consists of a frame B,
wedge C and a sliding rod A. So the three sliding pairs are, one between the wedge C
and the frame B, second between wedge C and sliding rod A and the frame B.
This figure shows the mechanism of a fly press. The element B forms a sliding with A
and turning pair with screw rod C which in turn forms a screw pair with A. When link
A is fixed, the required fly press mechanism is obtained.

11. 2. Kutzbach criterion, Grashoff's law
Kutzbach criterion:
 Fundamental Equation for 2-D Mechanisms: M = 3(L – 1) – 2J1 – J2
Can we intuitively derive Kutzbach’s modification of Grubler’s equation?
Consider a rigid link constrained to move in a plane. How many degrees of
freedom does the link have? (3: translation in x and y directions, rotation
about z-axis)
 If you pin one end of the link to the plane, how many degrees of freedom does
it now have?
 Add a second link to the picture so that you have one link pinned to the plane
and one free to move in the plane. How many degrees of freedom exist
between the two links? (4 is the correct answer)
 Pin the second link to the free end of the first link. How many degrees of
freedom do you now have?
 How many degrees of freedom do you have each time you introduce a moving
link? How many degrees of freedom do you take away when you add a
simple joint? How many degrees of freedom would you take away by adding
a half joint? Do the different terms in equation make sense in light of this
knowledge?
Grashoff's law:
 Grashoff 4-bar linkage: A linkage that contains one or more links capable
of undergoing a full rotation. A linkage is Grashoff if: S + L < P + Q (where:
S = shortest link length, L = longest, P, Q = intermediate length links). Both
joints of the shortest link are capable of 360 degrees of rotation in a Grashoff
linkages. This gives us 4 possible linkages: crank-rocker (input rotates 360),
rocker-crank-rocker (coupler rotates 360), rocker-crank (follower); double
crank (all links rotate 360). Note that these mechanisms are simply the
possible inversions (section 2.11, Figure 2-16) of a Grashoff mechanism.
 Non Grashoff 4 bar: No link can rotate 360 if: S + L > P + Q
Let’s examine why the Grashoff condition works:
 Consider a linkage with the shortest and longest sides joined together.
Examine the linkage when the shortest side is parallel to the longest side (2
positions possible, folded over on the long side and extended away from the
long side). How long do P and Q have to be to allow the linkage to achieve
these positions?
 Consider a linkage where the long and short sides are not joined. Can you
figure out the required lengths for P and Q in this type of mechanism
3. Kinematic Inversions of 4-bar chain and slider crank chains:
 Types of Kinematic Chain: 1) Four bar chain 2) Single slider chain 3) Double
Slider chain
 Four bar Chain:
The chain has four links and it looks like a cycle frame and hence it is also called
quadric cycle chain. It is shown in the figure. In this type of chain all four pairs will
be turning pairs.

12.  Inversions:
By fixing each link at a time we get as many mechanisms as the number of links, then
each mechanism is called ‘Inversion’ of the original Kinematic Chain.
Inversions of four bar chain mechanism:
There are three inversions: 1) Beam Engine or Crank and lever mechanism. 2)
Coupling rod of locomotive or double crank mechanism. 3) Watt’s straight line
mechanism or double lever mechanism.
 Beam Engine:
When the crank AB rotates about A, the link CE pivoted at D makes vertical
reciprocating motion at end E. This is used to convert rotary motion to reciprocating
motion and vice versa. It is also known as Crank and lever mechanism. This
mechanism is shown in the figure below.
 2. Coupling rod of locomotive: In this mechanism the length of link AD =
length of link C. Also length of link AB = length of link CD. When AB rotates about
A, the crank DC rotates about D. this mechanism is used for coupling locomotive
wheels. Since links AB and CD work as cranks, this mechanism is also known as
double crank mechanism. This is shown in the figure below.

13.  3. Watt’s straight line mechanism or Double lever mechanism: In this
mechanism, the links AB & DE act as levers at the ends A & E of these levers are
fixed. The AB & DE are parallel in the mean position of the mechanism and coupling
rod BD is perpendicular to the levers AB & DE. On any small displacement of the
mechanism the tracing point ‘C’ traces the shape of number ‘8’, a portion of which
will be approximately straight. Hence this is also an example for the approximate
straight line mechanism. This mechanism is shown below.
 2. Slider crank Chain:
It is a four bar chain having one sliding pair and three turning pairs. It is shown in the
figure below the purpose of this mechanism is to convert rotary motion to
reciprocating motion and vice versa.
Inversions of a Slider crank chain:
There are four inversions in a single slider chain mechanism. They are:
1) Reciprocating engine mechanism (1
st
inversion)
2) Oscillating cylinder engine mechanism (2
nd
inversion)
3) Crank and slotted lever mechanism (2
nd
inversion)
4) Whitworth quick return motion mechanism (3
rd
inversion)
5) Rotary engine mechanism (3
rd
inversion)
6) Bull engine mechanism (4
th
inversion)
7) Hand Pump (4
th
inversion)
 1. Reciprocating engine mechanism :
In the first inversion, the link 1 i.e., the cylinder and the frame is kept fixed. The fig
below shows a reciprocating engine.

14. A slotted link 1 is fixed. When the crank 2 rotates about O, the sliding piston 4
reciprocates in the slotted link 1. This mechanism is used in steam engine, pumps,
compressors, I.C. engines, etc.
 2. Crank and slotted lever mechanism:
It is an application of second inversion. The crank and slotted lever mechanism is
shown in figure below.
In this mechanism link 3 is fixed. The slider (link 1) reciprocates in oscillating slotted
lever (link 4) and crank (link 2) rotates. Link 5 connects link 4 to the ram (link 6). The
ram with the cutting tool reciprocates perpendicular to the fixed link 3. The ram with
the tool reverses its direction of motion when link 2 is perpendicular to link 4. Thus
the cutting stroke is executed during the rotation of the crank through angle α and the
return stroke is executed when the crank rotates through angle β or 360 – α.
Therefore, when the crank rotates uniformly, we get,
Time to cutting = α = α
Time of return β 360 – α
This mechanism is used in shaping machines, slotting machines and in rotary engines.
 3. Whitworth quick return motion mechanism:
Third inversion is obtained by fixing the crank i.e. link 2. Whitworth quick return
mechanism is an application of third inversion. This mechanism is shown in the figure
below. The crank OC is fixed and OQ rotates about O. The slider slides in the slotted
link and generates a circle of radius CP. Link 5 connects the extension OQ provided
on the opposite side of the link 1 to the ram (link 6). The rotary motion of P is taken
to the ram R which reciprocates. The quick return motion mechanism is used in
shapers and slotting machines. The angle covered during cutting stroke from P1 to P2
in counter clockwise direction is α or 360 -2θ. During the return stroke, the angle
covered is 2θ or β.

15. Therefore, Time to cutting = 360 -2θ = 180 – θ
Time of return 2θθ = α = α . β 360 – α
 4. Rotary engine mechanism or Gnome Engine:
Rotary engine mechanism or gnome engine is another application of third inversion. It
is a rotary cylinder V – type internal combustion engine used as an aero – engine. But
now Gnome engine has been replaced by Gas turbines. The Gnome engine has
generally seven cylinders in one plane. The crank OA is fixed and all the connecting
rods from the pistons are connected to A. In this mechanism when the pistons
reciprocate in the cylinders, the whole assembly of cylinders, pistons and connecting
rods rotate about the axis O, where the entire mechanical power developed, is
obtained in the form of rotation of the crank shaft. This mechanism is shown in the
figure below.
 Double Slider Crank Chain:
A four bar chain having two turning and two sliding pairs such that two pairs of the
same kind are adjacent is known as double slider crank chain.
 Inversions of Double slider Crank chain:
It consists of two sliding pairs and two turning pairs. They are three important
inversions of double slider crank chain. 1) Elliptical trammel. 2) Scotch yoke
mechanism. 3) Oldham’s Coupling.
 1. Elliptical Trammel:
This is an instrument for drawing ellipses. Here the slotted link is fixed. The sliding
block P and Q in vertical and horizontal slots respectively. The end R generates an
ellipse with the displacement of sliders P and Q.
The co-ordinates of the point R are x and y. From the fig. cos θ = x. PR
and Sin θ = y. QR
Squaring and adding (i) and (ii) we get x2
+ y2
= cos2
θ + sin2
θ
(PR)
2
(QR)
2

16. x2
+ y2
= 1
(PR)
2
(QR)
2
The equation is that of an ellipse, Hence the instrument traces an ellipse. Path traced
by mid-point of PQ is a circle. In this case, PR = PQ and so x
2
+y
2
=1 (PR)
2
(QR)
2
It is an equation of circle with PR = QR = radius of a circle.
 2. Scotch yoke mechanism: This mechanism, the slider P is fixed. When PQ
rotates above P, the slider Q reciprocates in the vertical slot. The mechanism is used
to convert rotary to reciprocating mechanism.
 3. Oldham’s coupling: The third inversion of obtained by fixing the link
connecting the 2 blocks P & Q. If one block is turning through an angle, the frame
and the other block will also turn through the same angle. It is shown in the figure
below.
An application of the third inversion of the double slider crank mechanism is
Oldham’s coupling shown in the figure. This coupling is used for connecting two
parallel shafts when the distance between the shafts is small. The two shafts to be
connected have flanges at their ends, secured by forging. Slots are cut in the flanges.
These flanges form 1 and 3. An intermediate disc having tongues at right angles and
opposite sides is fitted in between the flanges. The intermediate piece forms the link 4
which slides or reciprocates in flanges 1 & 3. The link two is fixed as shown. When
flange 1 turns, the intermediate disc 4 must turn through the same angle and whatever
angle 4 turns, the flange 3 must turn through the same angle. Hence 1, 4 & 3 must
have the same angular velocity at every instant. If the distance between the axis of the
shaft is x, it will be the diameter if the circle traced by the centre of the intermediate
piece. The maximum sliding speed of each tongue along its slot is given by
v=xω where, ω = angular velocity of each shaft in rad/sec v = linear velocity in m/sec
4. Mechanical Advantage, Transmission angle:
 The mechanical advantage (MA) is defined as the ratio of output torque to the
input torque. (or) ratio of load to output.
 Transmission angle.

17.  The extreme values of the transmission angle occur when the crank lies along
the line of frame.
5. Description of common mechanisms-Single, Double and offset slider
mechanisms - Quick return mechanisms:
 Quick Return Motion Mechanisms:
Many a times mechanisms are designed to perform repetitive operations. During these
operations for a certain period the mechanisms will be under load known as working
stroke and the remaining period is known as the return stroke, the mechanism returns
to repeat the operation without load. The ratio of time of working stroke to that of the
return stroke is known a time ratio. Quick return mechanisms are used in machine
tools to give a slow cutting stroke and a quick return stroke. The various quick return
mechanisms commonly used are i) Whitworth ii) Drag link. iii) Crank and slotted
lever mechanism
 1. Whitworth quick return mechanism:
Whitworth quick return mechanism is an application of third inversion of the single
slider crank chain. This mechanism is shown in the figure below. The crank OC is
fixed and OQ rotates about O. The slider slides in the slotted link and generates a
circle of radius CP. Link 5 connects the extension OQ provided on the opposite side
of the link 1 to the ram (link 6). The rotary motion of P is taken to the ram R which
reciprocates. The quick return motion mechanism is used in shapers and slotting
machines.
The angle covered during cutting stroke from P1 to P2 in counter clockwise direction
is α or 360 -2θ. During the return stroke, the angle covered is 2θ or β.
 2. Drag link mechanism :
This is four bar mechanism with double crank in which the shortest link is fixed. If
the crank AB rotates at a uniform speed, the crank CD rotate at a non-uniform speed.
This rotation of link CD is transformed to quick return reciprocatory motion of the
ram E by the link CE as shown in figure. When the crank AB rotates through an angle
α in Counter clockwise direction during working stroke, the link CD rotates through

18. 180. We can observe that / α >/ β. Hence time of working stroke is α /β times more or
the return stroke is α /β times quicker. Shortest link is always stationary link. Sum of
the shortest and the longest links of the four links 1, 2, 3 and 4 are less than the sum of
the other two. It is the necessary condition for the drag link quick return mechanism.
 3. Crank and slotted lever mechanism:
It is an application of second inversion. The crank and slotted lever mechanism is
shown in figure below.
In this mechanism link 3 is fixed. The slider (link 1) reciprocates in oscillating slotted
lever (link 4) and crank (link 2) rotates. Link 5 connects link 4 to the ram (link 6). The
ram with the cutting tool reciprocates perpendicular to the fixed link 3. The ram with
the tool reverses its direction of motion when link 2 is perpendicular to link 4. Thus
the cutting stroke is executed during the rotation of the crank through angle α and the
return stroke is executed when the crank rotates through angle β or 360 – α.
Therefore, when the crank rotates uniformly, we get,
Time to cutting = α = α
Time of return β 360 – α
This mechanism is used in shaping machines, slotting machines and in rotary engines.
6. Ratchets and escapements - Indexing Mechanisms - Rocking Mechanisms:
 Intermittent motion mechanism:
 1. Ratchet and Pawl mechanism: This mechanism is used in producing
intermittent rotary motion member. A ratchet and Pawl mechanism consists of a
ratchet wheel 2 and a pawl 3 as shown in the figure. When the lever 4 carrying pawl is
raised, the ratchet wheel rotates in the counter clock wise direction (driven by pawl).
As the pawl lever is lowered the pawl slides over the ratchet teeth. One more pawl 5 is
used to prevent the ratchet from reversing. Ratchets are used in feed mechanisms,
lifting jacks, clocks, watches and counting devices.
 2. Geneva mechanism: Geneva mechanism is an intermittent motion

19. mechanism. It consists of a driving wheel D carrying a pin P which engages in a slot
of follower F as shown in figure. During one quarter revolution of the driving plate,
the Pin and follower remain in contact and hence the follower is turned by one quarter
of a turn. During the remaining time of one revolution of the driver, the follower
remains in rest locked in position by the circular arc.
 3. Pantograph: Pantograph is used to copy the curves in reduced or enlarged
scales. Hence this mechanism finds its use in copying devices such as engraving or
profiling machines.
This is a simple figure of a Pantograph. The links are pin jointed at A, B, C and D.
AB is parallel to DC and AD is parallel to BC. Link BA is extended to fixed pin O. Q
is a point on the link AD. If the motion of Q is to be enlarged then the link BC is
extended to P such that O, Q and P are in a straight line. Then it can be shown that the
points P and Q always move parallel and similar to each other over any path straight
or curved. Their motions will be proportional to their distance from the fixed point.
Let ABCD be the initial position. Suppose if point Q moves to Q1 , then all the links
and the joints will move to the new positions (such as A moves to A1 , B moves to
Q1, C moves to Q1 , D moves to D1 and P to P1 ) and the new configuration of the
mechanism is shown by dotted lines. The movement of Q (Q Q1) will be enlarged to
PP1 in a definite ratio.
ELLIPTICAL TRAMMEL
This fascinating mechanism converts
rotary motion to reciprocating motion
in two axis. Notice that the handle
traces out an ellipse rather than a circle.
A similar mechanism is used
in ellipse
drawingtools.

20. 5. Hooke’s joint:
Hooke’s joint used to connect two parallel intersecting shafts as shown in figure. This
can also be used for shaft with angular misalignment where flexible coupling does not
serve the purpose. Hence Hooke’s joint is a means of connecting two rotating shafts
whose axes lie in the same plane and their directions making a small angle with each
other. It is commonly known as Universal joint. In Europe it is called as Cardan joint.
Straight line generators, Design of Crank-rocker Mechanisms:
 Straight Line Motion Mechanisms:
The easiest way to generate a straight line motion is by using a sliding pair but in
precision machines sliding pairs are not preferred because of wear and tear. Hence in
such cases different methods are used to generate straight line motion mechanisms:
1. Exact straight line motion mechanism.
a. Peaucellier mechanism, b. Hart mechanism, c. Scott Russell mechanism
2. Approximate straight line motion mechanisms
a. Watt mechanism, b. Grasshopper’s mechanism, c. Robert’s mechanism,
d. Tchebicheff’s mechanism
 a. Peaucillier mechanism :
The pin Q is constrained to move long the circumference of a circle by means of the
link OQ. The link OQ and the fixed link are equal in length. The pins P and Q are on
opposite corners of a four bar chain which has all four links QC, CP, PB and BQ of
equal length to the fixed pin A. i.e., link AB = link AC. The product AQ x AP remain
constant as the link OQ rotates may be proved as follows: Join BC to bisect PQ at F;
then, from the right angled triangles AFB, BFP, we have AB=AF+FB and
BP=BF+FP. Subtracting, AB-BP= AF-FP=(AF–FP)(AF+FP) = AQ x AP .
Since AB and BP are links of a constant length, the product AQ x AP is constant.
Therefore the point P traces out a straight path normal to AR.
 b. Robert’s mechanism:
This is also a four bar chain. The link PQ and RS are of equal length and the tracing
pint ‘O’ is rigidly attached to the link QR on a line which bisects QR at right angles.
The best position for O may be found by making use of the instantaneous centre of
QR. The path of O is clearly approximately horizontal in the Robert’s mechanism.
b. Hart mechanism
a. Peaucillier mechanism b. Hart mechanism

21. 80
Theory of Machines Objectives
After studying this unit, you should be able to
 understand power transmission derives,
 understand law of belting,
 determine power transmitted by belt drive and gear,
 determine dimensions of belt for given power to be transmitted,
 understand kinematics of chain drive,
 determine gear ratio for different type of gear trains,
 classify gears, and
 understand gear terminology.
3.2 POWER TRANSMISSION DEVICES
Power transmission devices are very commonly used to transmit power from one shaft to
another. Belts, chains and gears are used for this purpose. When the distance between the
shafts is large, belts or ropes are used and for intermediate distance chains can be used.
For belt drive distance can be maximum but this should not be more than ten metres for
good results. Gear drive is used for short distances.
3.2.1 Belts
In case of belts, friction between the belt and pulley is used to transmit power. In
practice, there is always some amount of slip between belt and pulleys, therefore, exact
velocity ratio cannot be obtained. That is why, belt drive is not a positive drive.
Therefore, the belt drive is used where exact velocity ratio is not required.
The following types of belts shown in Figure 3.1 are most commonly used :
(a) Flat Belt and Pulley (b) V-belt and Pulley (c) Circular Belt or Rope Pulley
Figure 3.1 : Types of Belt and Pulley
The flat belt is rectangular in cross-section as shown in Figure 3.1(a). The pulley for this
belt is slightly crowned to prevent slip of the belt to one side. It utilises the friction
between the flat surface of the belt and pulley.
The V-belt is trapezoidal in section as shown in Figure 3.1(b). It utilizes the force of
friction between the inclined sides of the belt and pulley. They are preferred when
distance is comparative shorter. Several V-belts can also be used together if power
transmitted is more.
The circular belt or rope is circular in section as shown in Figure 8.1(c). Several ropes
also can be used together to transmit more power.
The belt drives are of the following types :
(a) open belt drive, and
(b) cross belt drive.
Open Belt Drive
Open belt drive is used when sense of rotation of both the pulleys is same. It is
desirable to keep the tight side of the belt on the lower side and slack side at the

22. 81
Power Transmission
Devices
top to increase the angle of contact on the pulleys. This type of drive is shown in
Figure 3.2.
Figure 3.2 : Open Belt Derive
Cross Belt Drive
In case of cross belt drive, the pulleys rotate in the opposite direction. The angle of
contact of belt on both the pulleys is equal. This drive is shown in Figure 3.3. As
shown in the figure, the belt has to bend in two different planes. As a result of this,
belt wears very fast and therefore, this type of drive is not preferred for power
transmission. This can be used for transmission of speed at low power.
Figure 3.3 : Cross Belt Drive
Since power transmitted by a belt drive is due to the friction, belt drive is
subjected to slip and creep.
Let d1 and d2 be the diameters of driving and driven pulleys, respectively. N1 and
N2 be the corresponding speeds of driving and driven pulleys, respectively.
The velocity of the belt passing over the driver
1 1
1
60
d N
V


If there is no slip between the belt and pulley
2 2
1 2
60
d N
V V

 
or, 1 1 2 2
60 60
d N d N
 

or, 1 2
2 1
N d
N d

If thickness of the belt is ‘t’, and it is not negligible in comparison to the diameter,
1 2
2 1
N d t
N d t



Let there be total percentage slip ‘S’ in the belt drive which can be taken into
account as follows :
2 1 1
100
 
 
 
 
S
V V
or 2 2 1 1
1
60 60 100
   
 
 
 
d N d N S
Driving
Pulley
Slack Side Thickness
Effective Radius
Driving
Pulley
Neutral Section
Tight Side

23. 82
Theory of Machines If the thickness of belt is also to be considered
or 1 2
2 1
( ) 1
( )
1
100
N d t
S
N d t

 
  

 
 
or, 2 1
1 2
( )
1
( ) 100
N d t S
N d t
  
  
 
  
The belt moves from the tight side to the slack side and vice-versa, there is some
loss of power because the length of belt continuously extends on tight side and
contracts on loose side. Thus, there is relative motion between the belt and pulley
due to body slip. This is known as creep.
3.2.2 Chain
The belt drive is not a positive drive because of creep and slip. The chain drive is a
positive drive. Like belts, chains can be used for larger centre distances. They are made
of metal and due to this chain is heavier than the belt but they are flexible like belts. It
also requires lubrication from time to time. The lubricant prevents chain from rusting
and reduces wear.
The chain and chain drive are shown in Figure 3.4. The sprockets are used in place of
pulleys. The projected teeth of sprockets fit in the recesses of the chain. The distance
between roller centers of two adjacent links is known as pitch. The circle passing
through the pitch centers is called pitch circle.
(a) (b)
(c) (d)
Figure 3.4 : Chain and Chain Drive
Let ‘’ be the angle made by the pitch of the chain, and
‘r’ be the pitch circle radius, then
pitch, 2 sin
2
p r


or, cosec
2 2
p
r


The power transmission chains are made of steel and hardened to reduce wear. These
chains are classified into three categories
(a) Block chain
(b) Roller chain
(c) Inverted tooth chain (silent chain)
Pin
Pitch
Pitch
Roller
Bushing
Sprocket
r
φ
p

24. 83
Power Transmission
Devices
Out of these three categories roller chain shown in Figure 3.4(b) is most commonly used.
The construction of this type of chain is shown in the figure. The roller is made of steel
and then hardened to reduce the wear. A good roller chain is quiter in operation as
compared to the block chain and it has lesser wear. The block chain is shown in
Figure 3.4(a). It is used for low speed drive. The inverted tooth chain is shown in
Figures 3.4(c) and (d). It is also called as silent chain because it runs very quietly even at
higher speeds.
3.2.3 Gears
Gears are also used for power transmission. This is accomplished by the successive
engagement of teeth. The two gears transmit motion by the direct contact like chain
drive. Gears also provide positive drive.
The drive between the two gears can be represented by using plain cylinders or discs 1
and 2 having diameters equal to their pitch circles as shown in Figure 3.5. The point of
contact of the two pitch surfaces shell have velocity along the common tangent. Because
there is no slip, definite motion of gear 1 can be transmitted to gear 2 or vice-versa.
The tangential velocity ‘Vp’ = 1 r1 = 2 r2
where r1 and r2 are pitch circle radii of gears 1 and 2, respectively.
Figure 3.5 : Gear Drive
or, 1 2
1 2
2 2
60 60
N N
r r
 

or, 1 1 2 2
N r N r

or, 1 2
2 1
N r
N r

Since, pitch circle radius of a gear is proportional to its number of teeth (t).
 1 2
2 1
N t
N t

where t1 and t2 are the number of teeth on gears 1 and 2, respectively.
SAQ 1
In which type of drive centre distance between the shafts is lowest? Give reason
for this?
3.3 TRANSMISSION SCREW
In a screw, teeth are cut around its circular periphery which form helical path. A nut has
similar internal helix in its bore. When nut is turned on the screw with a force applied
tangentially, screw moves forward. For one turn, movement is equal to one lead. In case
of lead screw, screw rotates and nut moves along the axis over which tool post is
mounted.
N1
N2
2
1
VP

25. 84
Theory of Machines Let dm be the mean diameter of the screw,
 be angle of friction, and
p be the pitch.
If one helix is unwound, it will be similar to an inclined plane for which the angle of
inclination ‘’ is given by (Figure 3.6)
tan  

L
dm
For single start L = p
 tan  

p
dm
If force acting along the axis of the screw is W, effort applied tangential to the screw
(as discussed in Unit 2)
tan ( )
   
P W
for motion against force.
Also tan ( )
   
P W
for motion in direction of force.
Figure 3.6 : Transmission Screw
3.3.1 Power Transmitted
Torque acting on the screw
tan ( )
2 2
    
dm W dm
T P
If speed is N rpm
Power transmitted
2
watt
60


T N
tan ( )
2 kW
2 60 1000
  
  
 
W dm
N
3.4 POWER TRANSMISSION BY BELTS
In this section, we shall discuss how power is transmitted by a belt drive. The belts are
used to transmit very small power to the high amount of power. In some cases magnitude
of the power is negligible but the transmission of speed only may be important. In such
cases the axes of the two shafts may not be parallel. In some cases to increase the angle
L = p
W
P
 dm

26. 85
Power Transmission
Devices
of lap on the smaller pulley, the idler pulley is used. The angle of lap may be defined as
the angle of contact between the belt and the pulley. With the increase in angle of lap,
the belt drive can transmit more power. Along with the increase in angle of lap, the idler
pulley also does not allow reduction in the initial tension in the belt. The use of idler
pulley is shown in Figure 3.7.
Figure 3.7 : Use of Idler in Belt Drive
SAQ 2
(a) What is the main advantage of idler pulley?
(b) A prime mover drives a dc generator by belt drive. The speeds of prime
mover and generator are 300 rpm and 500 rpm, respectively. The diameter
of the driver pulley is 600 mm. The slip in the drive is 3%. Determine
diameter of the generator pulley if belt is 6 mm thick.
3.4.1 Law of Belting
The law of belting states that the centre line of the belt as it approaches the pulley, must
lie in plane perpendicular to the axis of the pulley in the mid plane of the pulley
otherwise the belt will run off the pulley. However, the point at which the belt leaves the
other pulley must lie in the plane of a pulley.
The Figure 3.8 below shows the belt drive in which two pulleys are at right angle to each
other. It can be seen that the centre line of the belt approaching larger or smaller pulley
lies in its plane. The point at which the belt leaves is contained in the plane of the other
pulley.
If motion of the belt is reversed, the law of the belting will be violated. Therefore,
motion is possible in one direction in case of non-parallel shafts as shown in Figure 3.8.
Figure 3.8 : Law of Belting
Idler Pulley

27. 86
Theory of Machines 3.4.2 Length of the Belt
For any type of the belt drive it is always desirable to know the length of belt required. It
will be required in the selection of the belt. The length can be determined by the
geometric considerations. However, actual length is slightly shorter than the theoretically
determined value.
Open Belt Drive
The open belt drive is shown in Figure 3.9. Let O1 and O2 be the pulley centers
and AB and CD be the common tangents on the circles representing the two
pulleys. The total length of the belt ‘L’ is given by
L = AB + Arc BHD + DC + Arc CGA
Let r be the radius of the smaller pulley,
R be the radius of the larger pulley,
C be the centre distance between the pulleys, and
 be the angle subtended by the tangents AB and CD with O1 O2.
Figure 3.9 : Open Belt Drive
Draw O1 N parallel to CD to meet O2 D at N.
By geometry,  O2 O1, N =  C O1 J =  D O2 K= 
Arc BHD = ( + 2) R,
Arc CGA = (  2) r
AB = CD = O1 N = O1 O2 cos  = C cos 
sin
R r
C

 
or, 1 ( )
sin
R r
C
 
 
2 2
1
cos 1 sin 1 sin
2
 
     
 
 
 2
1
( 2 ) ( 2 ) 2 1 sin
2
L R r C
 
          
 
 
For small value of ;
( )
R r
C

  , the approximate lengths
2
( ) 1
( ) 2 ( ) 2 1
2
R r R r
L R r R r C
C C
 
 
 
      
 
 
 
 
 
2
2
( ) 1
( ) 2 1
2
R r R r
R r C
C C
 
 
 
     
 
 
 
 
 
This provides approximate length because of the approximation taken earlier.
D K
C
A
B
G
C J
β
=
r
β
O1 O2
R
N
H
β

28. 87
Power Transmission
Devices
Crossed-Belt Drive
The crossed-belt drive is shown in Figure 3.10. Draw O1 N parallel to the line CD
which meets extended O2 D at N. By geometry
1 2 2 1
CO J DO K O O N
    
Arc Arc
L AGC AB BKD CD
   
Arc ( 2 ), and Arc ( 2 )
AGC r BKD R
       
1 ( )
sin or sin
R r R r
C C

 
   
For small value of 
R r
C


2
2 2
2
1 1 ( )
cos 1 sin 1 sin 1
2 2
R r
C
 

 
       
 
 
   
 
( 2 ) 2 cos ( 2 )
L r C R
         
( 2 ) ( ) 2 cos
R r C
      
Figure 3.10 : Cross Belt Drive
For approximate length
2 2
2
( ) 1 ( )
( ) 2 2 1
2
R r R r
L R r C
C C
 
 
     
 
 
 
2
( )
( ) 2
R r
R r C
C

    
SAQ 3
Which type of drive requires longer length for same centre distance and size of
pulleys?
3.4.3 Cone Pulleys
Sometimes the driving shaft is driven by the motor which rotates at constant speed but
the driven shaft is designed to be driven at different speeds. This can be easily done by
using stepped or cone pulleys as shown in Figure 3.11. The cone pulley has different sets
of radii and they are selected such that the same belt can be used at different sets of the
cone pulleys.
A
G
C
J
β
r
D K
β
O1 O2
R
N
C
β
B

29. 88
Theory of Machines
Figure 3.11 : Cone Pulleys
Let Nd be the speed of the driving shaft which is constant.
Nn be the speed of the driven shaft when the belt is on nth step.
rn be the radius of the nth step of driving pulley.
Rn be the radius of the nth step of the driven pulley.
where n is an integer, 1, 2, . . .
The speed ratio is inversely proportional to the pulley radii
 1 1
1
d
N r
N R
 . . . (3.1)
For this first step radii r1 and R1 can be chosen conveniently.
For second pair 2 2
2
d
N r
N R
 , and similarly n n
d n
N r
N R
 .
In order to use same belt on all the steps, the length of the belt should be same
i.e. 1 2 . . . n
L L L
   . . . (3.2)
Thus, two equations are available – one provided by the speed ratio and other provided
by the length relation and for selected speed ratio, the two radii can be calculated. Also it
has to be kept in mind that the two pulleys are same. It is desirable that the speed ratios
should be in geometric progression.
Let k be the ratio of progression of speed.
 3
2
1 2 1
. . . n
n
N N
N
k
N N N 
  
 2
2 1 3 1
and
N k N N k N
 
 1 1 1
1
1
 
 
n n
n d
r
N k N k N
R
 2
3
2 1 1
2 1 3 1
and
 
r
r r r
k k
R R R R
Since, both the pulleys are made similar.
1
r3
R3
2 3
4
5

30. 89
Power Transmission
Devices
1
1 1 1
1 1 1
or n
n
n
r R r R
k
R r R r

 
or, 1
1
1
n
R
k
r

 . . . (3.3)
If radii R1 and r1 have been chosen, the above equations provides value of k or vice-
versa.
SAQ 4
How the speed ratios are selected for cone pulleys?
3.4.4 Ratio of Tensions
The belt drive is used to transmit power from one shaft to the another. Due to the friction
between the pulley and the belt one side of the belt becomes tight side and other
becomes slack side. We have to first determine ratio of tensions.
Flat Belt
Let tension on the tight side be ‘T1’ and the tension on the slack side be ‘T2’. Let
‘’ be the angle of lap and let ‘’ be the coefficient of friction between the belt
and the pulley. Consider an infinitesimal length of the belt PQ which subtend an
angle  at the centre of the pulley. Let ‘R’ be the reaction between the element
and the pulley. Let ‘T’ be tension on the slack side of the element, i.e. at point P
and let ‘(T + T)’ be the tension on the tight side of the element.
The tensions T and (T + T) shall be acting tangential to the pulley and thereby
normal to the radii OP and OQ. The friction force shall be equal to ‘R’ and its
action will be to prevent slipping of the belt. The friction force will act
tangentially to the pulley at the point S.
Figure 3.12 : Ratio of Tensions in Flat Belt
Considering equilibrium of the element at S and equating it to zero.
Resolving all the forces in the tangential direction
cos ( ) cos 0
2 2
R T T T
 
     
or, cos
2
R T

   . . . (3.4)
T + ST
R
R
S
Q
P
δ θ
O
T2
T
T1
θ
δ θ
2
δ θ
2

31. 90
Theory of Machines Resolving all the forces in the radial direction at S and equating it to zero.
sin ( ) sin 0
2 2
R T T T
 
    
or, (2 ) sin
2
R T T

  
Since  is very small, taking limits
 cos 1 and sin
2 2 2
  

 (2 )
2 2
R T T T T
 
      
Neglecting the product of the two infinitesimal quantities
2
T

 

 
 
which is
negligible in comparison to other quantities :
 R T 
Substituting the value of R and cos 1
2

in Eq. (3.4), we get
T T
   
or,
T
T

 
Taking limits on both sides as    0
dT
d
T
  
Integrating between limits, it becomes
1
2 0
T
T
dT
d
T

  
 
or, 1
2
ln
T
T
 
or, 1
2
T
e
T

 . . . (3.5)
V-belt or Rope
The V-belt or rope makes contact on the two sides of the groove as shown in
Figure 3.13.
(a) (b)
Figure 3.13 : Ratio of Tension in V-Belt
T + δ T
2 Rn sinα
S
Q
δ θ/2
2μ Rn
P
O
T2
T
T1
θ
δ θ/2
α
2α
Rn
α
Rn

32. 91
Power Transmission
Devices
Let the reaction be ‘Rn’ on each of the two sides of the groove. The resultant
reaction will be 2Rn sin  at point S.
Resolving all the forces tangentially in the Figure 3.13(b), we get
2 cos ( ) cos 0
2 2
n
R T T T
 
     
or, 2 cos
2
n
R T

   . . . (3.6)
Resolving all the forces radially, we get
2 sin sin ( ) sin
2 2
n
R T T T
 
    
(2 ) sin
2
T T

  
Since  is very small
sin
2 2
 
 2 sin (2 )
2 2
n
R T T T T
 
        
Neglecting the product of the two infinitesimal quantities
2 sin
n
R T
 
or,
2sin
n
T
R


Substituting the value of Rn and using the approximation cos 1
2

, in Eq. (3.6),
we get
sin
T
T

  

or,
sin
T
T
 
 

Taking the limits and integrating between limits, we get
1
2 0
sin
T
T
dT
d
T


 

 
or, 1
2
ln
sin
T
T

 

or, sin
1
2




T
e
T
. . . (3.7)
SAQ 5
(a) If a rope makes two full turn and one quarter turn how much will be angle
of lap?
(b) If smaller pulley has coefficient of friction 0.3 and larger pulley has
coefficient of friction 0.2. The angle of lap on smaller and larger pulleys are
160o
and 200o
which value of () should be used for ratio of tensions?

33. 92
Theory of Machines 3.4.5 Power Transmitted by Belt Drive
The power transmitted by the belt depends on the tension on the two sides and the belt
speed.
Let T1 be the tension on the tight side in ‘N’
T2 be the tension on the slack side in ‘N’, and
V be the speed of the belt in m/sec.
Then power transmitted by the belt is given by
Power 1 2
( ) Watt
P T T V
 
1 2
( )
kW
1000
T T V

 . . . (3.8)
or,
2
1
1
1
kW
1000
T
T V
T
P
 

 
 

If belt is on the point of slipping.
1
2
T
e
T


 1 (1 )
kW
1000
T e V
P


 . . . (3.9)
The maximum tension T1 depends on the capacity of the belt to withstand force. If
allowable stress in the belt is ‘t’ in ‘Pa’, i.e. N/m2
, then
1 ( ) N
t
T t b
    . . . (3.10)
where t is thickness of the belt in ‘m’ and b is width of the belt also in m.
The above equations can also be used to determine ‘b’ for given power and speed.
3.4.6 Tension due to Centrifugal Forces
The belt has mass and as it rotates along with the pulley it is subjected to centrifugal
forces. If we assume that no power is being transmitted and pulleys are rotating, the
centrifugal force will tend to pull the belt as shown in Figure 3.14(b) and, thereby, a
tension in the belt called centrifugal tension will be introduced.
(a) (b)
Figure 3.14 : Tension due to Centrifugal Foces
Let ‘TC’ be the centrifugal tension due to centrifugal force.
Let us consider a small element which subtends an angle  at the centre of the pulley.
Let ‘m’ be the mass of the belt per unit length of the belt in ‘kg/m’.
TC
TC
δ θ/2
r
δ θ/2
FC
TC
TC
δ θ

34. 93
Power Transmission
Devices
The centrifugal force ‘Fc’ on the element will be given by
2
( )
C
V
F r m
r
  
where V is speed of the belt in m/sec. and r is the radius of pulley in ‘m’.
Resolving the forces on the element normal to the tangent
2 sin 0
2
C C
F T

 
Since  is very small.
 sin
2 2
 
or, 2 0
2
C C
F T

 
or, C C
F T
 
Substituting for FC
2
C
m V
r T
r
  
or, 2
C
T m V
 . . . (3.11)
Therefore, considering the effect of the centrifugal tension, the belt tension on the tight
side when power is transmitted is given by
Tension of tight side 1
t C
T T T
  and tension on the slack side 2
s C
T T T
  .
The centrifugal tension has an effect on the power transmitted because maximum tension
can be only Tt which is
t t
T t b
   
 2
1 t
T t b m V
    
SAQ 6
What will be the centrifugal tension if mass of belt is zero?
3.4.7 Initial Tension
When a belt is mounted on the pulley some amount of initial tension say ‘T0’ is provided
in the belt, otherwise power transmission is not possible because a loose belt cannot
sustain difference in the tension and no power can be transmitted.
When the drive is stationary the total tension on both sides will be ‘2 T0’.
When belt drive is transmitting power the total tension on both sides will be (T1 + T2),
where T1 is tension on tight side, and T2 is tension on the slack side.
If effect of centrifugal tension is neglected.
0 1 2
2T T T
 

35. 94
Theory of Machines
or, 1 2
0
2
T T
T


If effect of centrifugal tension is considered, then
0 1 2 2
t s C
T T T T T T
    
or, 1 2
0
2
C
T T
T T

  . . . (3.12)
3.4.8 Maximum Power Transmitted
The power transmitted depends on the tension ‘T1’, angle of lap , coefficient of friction
‘’ and belt speed ‘V’. For a given belt drive, the maximum tension (Tt), angle of lap and
coefficient of friction shall remain constant provided that
(a) the tension on tight side, i.e. maximum tension should be equal to the
maximum permissible value for the belt, and
(b) the belt should be on the point of slipping.
Therefore, Power 1 (1 )
P T e
  V
Since, 1 t c
T T T
 
or, ( ) (1 )
t c
P T T e V

  
or, 2
( ) (1 )
t
P T m V e V

  
For maximum power transmitted
 2
( 3 ) (1 )
t
dP
T m V e
dV

  
or, 2
3 0
t
T m V
 
or, 3 0
 
t c
T T
or,
3
t
c
T
T 
or, 2
3
 t
T
m V
Also,
3
t
T
V
m
 . . . (3.13)
At the belt speed given by the Eq. (3.13) the power transmitted by the belt drive shall be
maximum.
SAQ 7
What is the value of centrifugal tension corresponding to the maximum power
transmitted?

36. 79
Power Transmission
Devices
UNIT 3 POWER TRANSMISSION DEVICES
Structure
3.1 Introduction
Objectives
3.2 Power Transmission Devices
3.2.1 Belts
3.2.2 Chain
3.2.3 Gears
3.3 Transmission Screw
3.4 Power Transmission by Belts
3.4.1 Law of Belting
3.4.2 Length of the Belt
3.4.3 Cone Pulleys
3.4.4 Ratio of Tensions
3.4.5 Power Transmitted by Belt Drive
3.4.6 Tension due to Centrifugal Forces
3.4.7 Initial Tension
3.4.8 Maximum Power Transmitted
3.5 Kinematics of Chain Drive
3.6 Classification of Gears
3.6.1 Parallel Shafts
3.6.2 Intersecting Shafts
3.6.3 Skew Shafts
3.7 Gear Terminology
3.8 Gear Train
3.8.1 Simple Gear Train
3.8.2 Compound Gear Train
3.8.3 Power Transmitted by Simple Spur Gear
3.9 Summary
3.10 Key Words
3.11 Answers to SAQs
3.1 INTRODUCTION
The power is transmitted from one shaft to the other by means of belts, chains and gears.
The belts and ropes are flexible members which are used where distance between the
two shafts is large. The chains also have flexibility but they are preferred for
intermediate distances. The gears are used when the shafts are very close with each
other. This type of drive is also called positive drive because there is no slip. If the
distance is slightly larger, chain drive can be used for making it a positive drive. Belts
and ropes transmit power due to the friction between the belt or rope and the pulley.
There is a possibility of slip and creep and that is why, this drive is not a positive drive.
A gear train is a combination of gears which are used for transmitting motion from one
shaft to another.

37. 80
Theory of Machines Objectives
After studying this unit, you should be able to
 understand power transmission derives,
 understand law of belting,
 determine power transmitted by belt drive and gear,
 determine dimensions of belt for given power to be transmitted,
 understand kinematics of chain drive,
 determine gear ratio for different type of gear trains,
 classify gears, and
 understand gear terminology.
3.2 POWER TRANSMISSION DEVICES
Power transmission devices are very commonly used to transmit power from one shaft to
another. Belts, chains and gears are used for this purpose. When the distance between the
shafts is large, belts or ropes are used and for intermediate distance chains can be used.
For belt drive distance can be maximum but this should not be more than ten metres for
good results. Gear drive is used for short distances.
3.2.1 Belts
In case of belts, friction between the belt and pulley is used to transmit power. In
practice, there is always some amount of slip between belt and pulleys, therefore, exact
velocity ratio cannot be obtained. That is why, belt drive is not a positive drive.
Therefore, the belt drive is used where exact velocity ratio is not required.
The following types of belts shown in Figure 3.1 are most commonly used :
(a) Flat Belt and Pulley (b) V-belt and Pulley (c) Circular Belt or Rope Pulley
Figure 3.1 : Types of Belt and Pulley
The flat belt is rectangular in cross-section as shown in Figure 3.1(a). The pulley for this
belt is slightly crowned to prevent slip of the belt to one side. It utilises the friction
between the flat surface of the belt and pulley.
The V-belt is trapezoidal in section as shown in Figure 3.1(b). It utilizes the force of
friction between the inclined sides of the belt and pulley. They are preferred when
distance is comparative shorter. Several V-belts can also be used together if power
transmitted is more.
The circular belt or rope is circular in section as shown in Figure 8.1(c). Several ropes
also can be used together to transmit more power.
The belt drives are of the following types :
(a) open belt drive, and
(b) cross belt drive.
Open Belt Drive
Open belt drive is used when sense of rotation of both the pulleys is same. It is
desirable to keep the tight side of the belt on the lower side and slack side at the

38. 81
Power Transmission
Devices
top to increase the angle of contact on the pulleys. This type of drive is shown in
Figure 3.2.
Figure 3.2 : Open Belt Derive
Cross Belt Drive
In case of cross belt drive, the pulleys rotate in the opposite direction. The angle of
contact of belt on both the pulleys is equal. This drive is shown in Figure 3.3. As
shown in the figure, the belt has to bend in two different planes. As a result of this,
belt wears very fast and therefore, this type of drive is not preferred for power
transmission. This can be used for transmission of speed at low power.
Figure 3.3 : Cross Belt Drive
Since power transmitted by a belt drive is due to the friction, belt drive is
subjected to slip and creep.
Let d1 and d2 be the diameters of driving and driven pulleys, respectively. N1 and
N2 be the corresponding speeds of driving and driven pulleys, respectively.
The velocity of the belt passing over the driver
1 1
1
60
d N
V


If there is no slip between the belt and pulley
2 2
1 2
60
d N
V V

 
or, 1 1 2 2
60 60
d N d N
 

or, 1 2
2 1
N d
N d

If thickness of the belt is ‘t’, and it is not negligible in comparison to the diameter,
1 2
2 1
N d t
N d t



Let there be total percentage slip ‘S’ in the belt drive which can be taken into
account as follows :
2 1 1
100
 
 
 
 
S
V V
or 2 2 1 1
1
60 60 100
   
 
 
 
d N d N S
Driving
Pulley
Slack Side Thickness
Effective Radius
Driving
Pulley
Neutral Section
Tight Side

39. 82
Theory of Machines If the thickness of belt is also to be considered
or 1 2
2 1
( ) 1
( )
1
100
N d t
S
N d t

 
  

 
 
or, 2 1
1 2
( )
1
( ) 100
N d t S
N d t
  
  
 
  
The belt moves from the tight side to the slack side and vice-versa, there is some
loss of power because the length of belt continuously extends on tight side and
contracts on loose side. Thus, there is relative motion between the belt and pulley
due to body slip. This is known as creep.
3.2.2 Chain
The belt drive is not a positive drive because of creep and slip. The chain drive is a
positive drive. Like belts, chains can be used for larger centre distances. They are made
of metal and due to this chain is heavier than the belt but they are flexible like belts. It
also requires lubrication from time to time. The lubricant prevents chain from rusting
and reduces wear.
The chain and chain drive are shown in Figure 3.4. The sprockets are used in place of
pulleys. The projected teeth of sprockets fit in the recesses of the chain. The distance
between roller centers of two adjacent links is known as pitch. The circle passing
through the pitch centers is called pitch circle.
(a) (b)
(c) (d)
Figure 3.4 : Chain and Chain Drive
Let ‘’ be the angle made by the pitch of the chain, and
‘r’ be the pitch circle radius, then
pitch, 2 sin
2
p r


or, cosec
2 2
p
r


The power transmission chains are made of steel and hardened to reduce wear. These
chains are classified into three categories
(a) Block chain
(b) Roller chain
(c) Inverted tooth chain (silent chain)
Pin
Pitch
Pitch
Roller
Bushing
Sprocket
r
φ
p

40. 83
Power Transmission
Devices
Out of these three categories roller chain shown in Figure 3.4(b) is most commonly used.
The construction of this type of chain is shown in the figure. The roller is made of steel
and then hardened to reduce the wear. A good roller chain is quiter in operation as
compared to the block chain and it has lesser wear. The block chain is shown in
Figure 3.4(a). It is used for low speed drive. The inverted tooth chain is shown in
Figures 3.4(c) and (d). It is also called as silent chain because it runs very quietly even at
higher speeds.
3.2.3 Gears
Gears are also used for power transmission. This is accomplished by the successive
engagement of teeth. The two gears transmit motion by the direct contact like chain
drive. Gears also provide positive drive.
The drive between the two gears can be represented by using plain cylinders or discs 1
and 2 having diameters equal to their pitch circles as shown in Figure 3.5. The point of
contact of the two pitch surfaces shell have velocity along the common tangent. Because
there is no slip, definite motion of gear 1 can be transmitted to gear 2 or vice-versa.
The tangential velocity ‘Vp’ = 1 r1 = 2 r2
where r1 and r2 are pitch circle radii of gears 1 and 2, respectively.
Figure 3.5 : Gear Drive
or, 1 2
1 2
2 2
60 60
N N
r r
 

or, 1 1 2 2
N r N r

or, 1 2
2 1
N r
N r

Since, pitch circle radius of a gear is proportional to its number of teeth (t).
 1 2
2 1
N t
N t

where t1 and t2 are the number of teeth on gears 1 and 2, respectively.
SAQ 1
In which type of drive centre distance between the shafts is lowest? Give reason
for this?
3.3 TRANSMISSION SCREW
In a screw, teeth are cut around its circular periphery which form helical path. A nut has
similar internal helix in its bore. When nut is turned on the screw with a force applied
tangentially, screw moves forward. For one turn, movement is equal to one lead. In case
of lead screw, screw rotates and nut moves along the axis over which tool post is
mounted.
N1
N2
2
1
VP

41. 84
Theory of Machines Let dm be the mean diameter of the screw,
 be angle of friction, and
p be the pitch.
If one helix is unwound, it will be similar to an inclined plane for which the angle of
inclination ‘’ is given by (Figure 3.6)
tan  

L
dm
For single start L = p
 tan  

p
dm
If force acting along the axis of the screw is W, effort applied tangential to the screw
(as discussed in Unit 2)
tan ( )
   
P W
for motion against force.
Also tan ( )
   
P W
for motion in direction of force.
Figure 3.6 : Transmission Screw
3.3.1 Power Transmitted
Torque acting on the screw
tan ( )
2 2
    
dm W dm
T P
If speed is N rpm
Power transmitted
2
watt
60


T N
tan ( )
2 kW
2 60 1000
  
  
 
W dm
N
3.4 POWER TRANSMISSION BY BELTS
In this section, we shall discuss how power is transmitted by a belt drive. The belts are
used to transmit very small power to the high amount of power. In some cases magnitude
of the power is negligible but the transmission of speed only may be important. In such
cases the axes of the two shafts may not be parallel. In some cases to increase the angle
L = p
W
P
 dm

42. 85
Power Transmission
Devices
of lap on the smaller pulley, the idler pulley is used. The angle of lap may be defined as
the angle of contact between the belt and the pulley. With the increase in angle of lap,
the belt drive can transmit more power. Along with the increase in angle of lap, the idler
pulley also does not allow reduction in the initial tension in the belt. The use of idler
pulley is shown in Figure 3.7.
Figure 3.7 : Use of Idler in Belt Drive
SAQ 2
(a) What is the main advantage of idler pulley?
(b) A prime mover drives a dc generator by belt drive. The speeds of prime
mover and generator are 300 rpm and 500 rpm, respectively. The diameter
of the driver pulley is 600 mm. The slip in the drive is 3%. Determine
diameter of the generator pulley if belt is 6 mm thick.
3.4.1 Law of Belting
The law of belting states that the centre line of the belt as it approaches the pulley, must
lie in plane perpendicular to the axis of the pulley in the mid plane of the pulley
otherwise the belt will run off the pulley. However, the point at which the belt leaves the
other pulley must lie in the plane of a pulley.
The Figure 3.8 below shows the belt drive in which two pulleys are at right angle to each
other. It can be seen that the centre line of the belt approaching larger or smaller pulley
lies in its plane. The point at which the belt leaves is contained in the plane of the other
pulley.
If motion of the belt is reversed, the law of the belting will be violated. Therefore,
motion is possible in one direction in case of non-parallel shafts as shown in Figure 3.8.
Figure 3.8 : Law of Belting
Idler Pulley

43. 86
Theory of Machines 3.4.2 Length of the Belt
For any type of the belt drive it is always desirable to know the length of belt required. It
will be required in the selection of the belt. The length can be determined by the
geometric considerations. However, actual length is slightly shorter than the theoretically
determined value.
Open Belt Drive
The open belt drive is shown in Figure 3.9. Let O1 and O2 be the pulley centers
and AB and CD be the common tangents on the circles representing the two
pulleys. The total length of the belt ‘L’ is given by
L = AB + Arc BHD + DC + Arc CGA
Let r be the radius of the smaller pulley,
R be the radius of the larger pulley,
C be the centre distance between the pulleys, and
 be the angle subtended by the tangents AB and CD with O1 O2.
Figure 3.9 : Open Belt Drive
Draw O1 N parallel to CD to meet O2 D at N.
By geometry,  O2 O1, N =  C O1 J =  D O2 K= 
Arc BHD = ( + 2) R,
Arc CGA = (  2) r
AB = CD = O1 N = O1 O2 cos  = C cos 
sin
R r
C

 
or, 1 ( )
sin
R r
C
 
 
2 2
1
cos 1 sin 1 sin
2
 
     
 
 
 2
1
( 2 ) ( 2 ) 2 1 sin
2
L R r C
 
          
 
 
For small value of ;
( )
R r
C

  , the approximate lengths
2
( ) 1
( ) 2 ( ) 2 1
2
R r R r
L R r R r C
C C
 
 
 
      
 
 
 
 
 
2
2
( ) 1
( ) 2 1
2
R r R r
R r C
C C
 
 
 
     
 
 
 
 
 
This provides approximate length because of the approximation taken earlier.
D K
C
A
B
G
C J
β
=
r
β
O1 O2
R
N
H
β

44. 87
Power Transmission
Devices
Crossed-Belt Drive
The crossed-belt drive is shown in Figure 3.10. Draw O1 N parallel to the line CD
which meets extended O2 D at N. By geometry
1 2 2 1
CO J DO K O O N
    
Arc Arc
L AGC AB BKD CD
   
Arc ( 2 ), and Arc ( 2 )
AGC r BKD R
       
1 ( )
sin or sin
R r R r
C C

 
   
For small value of 
R r
C


2
2 2
2
1 1 ( )
cos 1 sin 1 sin 1
2 2
R r
C
 

 
       
 
 
   
 
( 2 ) 2 cos ( 2 )
L r C R
         
( 2 ) ( ) 2 cos
R r C
      
Figure 3.10 : Cross Belt Drive
For approximate length
2 2
2
( ) 1 ( )
( ) 2 2 1
2
R r R r
L R r C
C C
 
 
     
 
 
 
2
( )
( ) 2
R r
R r C
C

    
SAQ 3
Which type of drive requires longer length for same centre distance and size of
pulleys?
3.4.3 Cone Pulleys
Sometimes the driving shaft is driven by the motor which rotates at constant speed but
the driven shaft is designed to be driven at different speeds. This can be easily done by
using stepped or cone pulleys as shown in Figure 3.11. The cone pulley has different sets
of radii and they are selected such that the same belt can be used at different sets of the
cone pulleys.
A
G
C
J
β
r
D K
β
O1 O2
R
N
C
β
B

45. 88
Theory of Machines
Figure 3.11 : Cone Pulleys
Let Nd be the speed of the driving shaft which is constant.
Nn be the speed of the driven shaft when the belt is on nth step.
rn be the radius of the nth step of driving pulley.
Rn be the radius of the nth step of the driven pulley.
where n is an integer, 1, 2, . . .
The speed ratio is inversely proportional to the pulley radii
 1 1
1
d
N r
N R
 . . . (3.1)
For this first step radii r1 and R1 can be chosen conveniently.
For second pair 2 2
2
d
N r
N R
 , and similarly n n
d n
N r
N R
 .
In order to use same belt on all the steps, the length of the belt should be same
i.e. 1 2 . . . n
L L L
   . . . (3.2)
Thus, two equations are available – one provided by the speed ratio and other provided
by the length relation and for selected speed ratio, the two radii can be calculated. Also it
has to be kept in mind that the two pulleys are same. It is desirable that the speed ratios
should be in geometric progression.
Let k be the ratio of progression of speed.
 3
2
1 2 1
. . . n
n
N N
N
k
N N N 
  
 2
2 1 3 1
and
N k N N k N
 
 1 1 1
1
1
 
 
n n
n d
r
N k N k N
R
 2
3
2 1 1
2 1 3 1
and
 
r
r r r
k k
R R R R
Since, both the pulleys are made similar.
1
r3
R3
2 3
4
5

46. 89
Power Transmission
Devices
1
1 1 1
1 1 1
or n
n
n
r R r R
k
R r R r

 
or, 1
1
1
n
R
k
r

 . . . (3.3)
If radii R1 and r1 have been chosen, the above equations provides value of k or vice-
versa.
SAQ 4
How the speed ratios are selected for cone pulleys?
3.4.4 Ratio of Tensions
The belt drive is used to transmit power from one shaft to the another. Due to the friction
between the pulley and the belt one side of the belt becomes tight side and other
becomes slack side. We have to first determine ratio of tensions.
Flat Belt
Let tension on the tight side be ‘T1’ and the tension on the slack side be ‘T2’. Let
‘’ be the angle of lap and let ‘’ be the coefficient of friction between the belt
and the pulley. Consider an infinitesimal length of the belt PQ which subtend an
angle  at the centre of the pulley. Let ‘R’ be the reaction between the element
and the pulley. Let ‘T’ be tension on the slack side of the element, i.e. at point P
and let ‘(T + T)’ be the tension on the tight side of the element.
The tensions T and (T + T) shall be acting tangential to the pulley and thereby
normal to the radii OP and OQ. The friction force shall be equal to ‘R’ and its
action will be to prevent slipping of the belt. The friction force will act
tangentially to the pulley at the point S.
Figure 3.12 : Ratio of Tensions in Flat Belt
Considering equilibrium of the element at S and equating it to zero.
Resolving all the forces in the tangential direction
cos ( ) cos 0
2 2
R T T T
 
     
or, cos
2
R T

   . . . (3.4)
T + ST
R
R
S
Q
P
δ θ
O
T2
T
T1
θ
δ θ
2
δ θ
2

47. 90
Theory of Machines Resolving all the forces in the radial direction at S and equating it to zero.
sin ( ) sin 0
2 2
R T T T
 
    
or, (2 ) sin
2
R T T

  
Since  is very small, taking limits
 cos 1 and sin
2 2 2
  

 (2 )
2 2
R T T T T
 
      
Neglecting the product of the two infinitesimal quantities
2
T

 

 
 
which is
negligible in comparison to other quantities :
 R T 
Substituting the value of R and cos 1
2

in Eq. (3.4), we get
T T
   
or,
T
T

 
Taking limits on both sides as    0
dT
d
T
  
Integrating between limits, it becomes
1
2 0
T
T
dT
d
T

  
 
or, 1
2
ln
T
T
 
or, 1
2
T
e
T

 . . . (3.5)
V-belt or Rope
The V-belt or rope makes contact on the two sides of the groove as shown in
Figure 3.13.
(a) (b)
Figure 3.13 : Ratio of Tension in V-Belt
T + δ T
2 Rn sinα
S
Q
δ θ/2
2μ Rn
P
O
T2
T
T1
θ
δ θ/2
α
2α
Rn
α
Rn

48. 91
Power Transmission
Devices
Let the reaction be ‘Rn’ on each of the two sides of the groove. The resultant
reaction will be 2Rn sin  at point S.
Resolving all the forces tangentially in the Figure 3.13(b), we get
2 cos ( ) cos 0
2 2
n
R T T T
 
     
or, 2 cos
2
n
R T

   . . . (3.6)
Resolving all the forces radially, we get
2 sin sin ( ) sin
2 2
n
R T T T
 
    
(2 ) sin
2
T T

  
Since  is very small
sin
2 2
 
 2 sin (2 )
2 2
n
R T T T T
 
        
Neglecting the product of the two infinitesimal quantities
2 sin
n
R T
 
or,
2sin
n
T
R


Substituting the value of Rn and using the approximation cos 1
2

, in Eq. (3.6),
we get
sin
T
T

  

or,
sin
T
T
 
 

Taking the limits and integrating between limits, we get
1
2 0
sin
T
T
dT
d
T


 

 
or, 1
2
ln
sin
T
T

 

or, sin
1
2




T
e
T
. . . (3.7)
SAQ 5
(a) If a rope makes two full turn and one quarter turn how much will be angle
of lap?
(b) If smaller pulley has coefficient of friction 0.3 and larger pulley has
coefficient of friction 0.2. The angle of lap on smaller and larger pulleys are
160o
and 200o
which value of () should be used for ratio of tensions?

49. 92
Theory of Machines 3.4.5 Power Transmitted by Belt Drive
The power transmitted by the belt depends on the tension on the two sides and the belt
speed.
Let T1 be the tension on the tight side in ‘N’
T2 be the tension on the slack side in ‘N’, and
V be the speed of the belt in m/sec.
Then power transmitted by the belt is given by
Power 1 2
( ) Watt
P T T V
 
1 2
( )
kW
1000
T T V

 . . . (3.8)
or,
2
1
1
1
kW
1000
T
T V
T
P
 

 
 

If belt is on the point of slipping.
1
2
T
e
T


 1 (1 )
kW
1000
T e V
P


 . . . (3.9)
The maximum tension T1 depends on the capacity of the belt to withstand force. If
allowable stress in the belt is ‘t’ in ‘Pa’, i.e. N/m2
, then
1 ( ) N
t
T t b
    . . . (3.10)
where t is thickness of the belt in ‘m’ and b is width of the belt also in m.
The above equations can also be used to determine ‘b’ for given power and speed.
3.4.6 Tension due to Centrifugal Forces
The belt has mass and as it rotates along with the pulley it is subjected to centrifugal
forces. If we assume that no power is being transmitted and pulleys are rotating, the
centrifugal force will tend to pull the belt as shown in Figure 3.14(b) and, thereby, a
tension in the belt called centrifugal tension will be introduced.
(a) (b)
Figure 3.14 : Tension due to Centrifugal Foces
Let ‘TC’ be the centrifugal tension due to centrifugal force.
Let us consider a small element which subtends an angle  at the centre of the pulley.
Let ‘m’ be the mass of the belt per unit length of the belt in ‘kg/m’.
TC
TC
δ θ/2
r
δ θ/2
FC
TC
TC
δ θ

50. 93
Power Transmission
Devices
The centrifugal force ‘Fc’ on the element will be given by
2
( )
C
V
F r m
r
  
where V is speed of the belt in m/sec. and r is the radius of pulley in ‘m’.
Resolving the forces on the element normal to the tangent
2 sin 0
2
C C
F T

 
Since  is very small.
 sin
2 2
 
or, 2 0
2
C C
F T

 
or, C C
F T
 
Substituting for FC
2
C
m V
r T
r
  
or, 2
C
T m V
 . . . (3.11)
Therefore, considering the effect of the centrifugal tension, the belt tension on the tight
side when power is transmitted is given by
Tension of tight side 1
t C
T T T
  and tension on the slack side 2
s C
T T T
  .
The centrifugal tension has an effect on the power transmitted because maximum tension
can be only Tt which is
t t
T t b
   
 2
1 t
T t b m V
    
SAQ 6
What will be the centrifugal tension if mass of belt is zero?
3.4.7 Initial Tension
When a belt is mounted on the pulley some amount of initial tension say ‘T0’ is provided
in the belt, otherwise power transmission is not possible because a loose belt cannot
sustain difference in the tension and no power can be transmitted.
When the drive is stationary the total tension on both sides will be ‘2 T0’.
When belt drive is transmitting power the total tension on both sides will be (T1 + T2),
where T1 is tension on tight side, and T2 is tension on the slack side.
If effect of centrifugal tension is neglected.
0 1 2
2T T T
 

51. 94
Theory of Machines
or, 1 2
0
2
T T
T


If effect of centrifugal tension is considered, then
0 1 2 2
t s C
T T T T T T
    
or, 1 2
0
2
C
T T
T T

  . . . (3.12)
3.4.8 Maximum Power Transmitted
The power transmitted depends on the tension ‘T1’, angle of lap , coefficient of friction
‘’ and belt speed ‘V’. For a given belt drive, the maximum tension (Tt), angle of lap and
coefficient of friction shall remain constant provided that
(a) the tension on tight side, i.e. maximum tension should be equal to the
maximum permissible value for the belt, and
(b) the belt should be on the point of slipping.
Therefore, Power 1 (1 )
P T e
  V
Since, 1 t c
T T T
 
or, ( ) (1 )
t c
P T T e V

  
or, 2
( ) (1 )
t
P T m V e V

  
For maximum power transmitted
 2
( 3 ) (1 )
t
dP
T m V e
dV

  
or, 2
3 0
t
T m V
 
or, 3 0
 
t c
T T
or,
3
t
c
T
T 
or, 2
3
 t
T
m V
Also,
3
t
T
V
m
 . . . (3.13)
At the belt speed given by the Eq. (3.13) the power transmitted by the belt drive shall be
maximum.
SAQ 7
What is the value of centrifugal tension corresponding to the maximum power
transmitted?

52. 95
Power Transmission
Devices
3.5 KINEMATICS OF CHAIN DRIVE
The chain is wrapped round the sprocket as shown in Figure 3.4(d). The chain in motion
is shown in Figure 3.15. It may be observed that the position of axial line changes
between the two position as shown by the dotted line and full line. The dotted line meets
at point B when extended with the line of centers. The firm line meets the line of centers
at point A when extended. The speed of the driving sprocket say ‘1’ shall be constant
but the velocity of chain will vary between 1  O1 C and 1  O1 D. Therefore,
2 1
1 2
O A
O B



Figure 3.15 : Kinematics of Chain Drive
The variation in the chain speed causes the variation in the angular speed of the driven
sprocket. The angular speed of the driven sprocket will vary between
1 1
1 1
2 2
and
O B O A
O B O A
 
This variation can be reduced by increasing number of teeth on the sprocket.
3.6 CLASSIFICATION OF GEARS
There are different types of arrangement of shafts which are used in practice. According
to the relative positions of shaft axes, different types of gears are used.
3.6.1 Parallel Shafts
In this arrangement, the shaft axes lie in parallel planes and remain parallel to one
another. The following type of gears are used on these shafts :
Spur Gears
These gears have straight teeth with their alignment parallel to the axes. These
gears are shown in mesh in Figures 3.16(a) and (b). The contact between the two
meshing teeth is along a line whose length is equal to entire length of teeth. It may
be observed that in external meshing, the two shafts rotate opposite to each other
whereas in internal meshing the shafts rotate in the same sense.
(a) External Meshing (b) Internal Meshing
Figure 3.16 : Spur Gears
If the gears mesh externally and diameter of one gear becomes infinite, the
arrangement becomes ‘Spur Rack and Pinion’. This is shown in Figure 3.17. It
converts rotary motion into translatory motion, or vice-versa.
ώ1
ώ2
o1 o2
D
C
A B
Line
Contact
Line
Contact

53. 96
Theory of Machines
Figure 3.17 : Spur Rack and Pinion
Helical Gears or Helical Spur Gears
In helical gears, the teeth make an angle with the axes of the gears which is called
helix angle. The two meshing gears have same helix angle but its layout is in
opposite sense as shown in Figure 3.18.
Figure 3.18 : Helical Gears
The contact between two teeth occurs at a point of the leading edge. The point
moves along a diagonal line across the teeth. This results in gradual transfer of
load and reduction in impact load and thereby reduction in noise. Unlike spur
gears the helical gears introduce thrust along the axis of the shaft which is to be
borne by thrust bearings.
Double-Helical or Herringbone Gears
A double-helical gear is equivalent to a pair of helical gears having equal helix
angle secured together, one having a right-hand helix and the other a left-hand
helix. The teeth of two rows are separated by a groove which is required for tool
run out. The axial thrust which occurs in case of single-helical gears is eliminated
in double helical gears. If the left and right inclinations of a double helical gear
meet at a common apex and groove is eliminated in it, the gear is known as
herringbone gear as shown in Figure 3.19.
Figure 3.19 : Herringbone Gears
Line Contact
Drivern
Thrust
Thrust
Driver

54. 97
Power Transmission
Devices
3.6.2 Intersecting Shafts
The motion between two intersecting shafts is equivalent to rolling of two conical
frustums from kinematical point of view.
Straight Bevel Gears
These gears have straight teeth which are radial to the point of intersection of the
shaft axes. Their teeth vary in cross section through out their length. Generally,
they are used to connect shafts at right angles. These gears are shown in
Figure 3.20. The teeth make line contact like spur gears.
Figure 3.20 : Straight Bevel Gears
As a special case, gears of the same size and connecting two shafts at right angle
to each other are known as mitre gears.
Spiral Bevel Gears
When the teeth of a bevel gear are inclined at an angle to the face of the bevel,
these gears are known as spiral bevel gears or helical bevel gears. A gear of this
type is shown in Figure 3.21(a). They run quiter in action and have point contact.
If spiral bevel gear has curved teeth but with zero degree spiral angle, it is known
as zerol bevel gear.
(a) Spiral Bevel Gear (b) Zerol Bevel Gear
Figure 3.21 : Spiral Bevel Gears
3.6.3 Skew Shafts
These shafts are non-parallel and non-intersecting. The motion of the two mating gears is
equivalent to motion of two hyperboloids in contact as shown in Figure 3.22. The angle
between the two shafts is equal to the sum of the angles of the two hyperboloids. That is
1 2
    
The minimum perpendicular distance between the two shafts is equal to the sum of the
throat radii.
Figure 3.22 : Hyperboloids in Contact
Ψ2
Ψ1
θ
B
1
2
A
Line of
contact

55. 98
Theory of Machines Crossed-Helical Gears or Spiral Gears
They can be used for any two shafts at any angle as shown in Figure 3.23 by a
suitable choice of helix angle. These gears are used to drive feed mechanisms on
machine tool.
Figure 3.23 : Spiral Gears in Contact
Worm Gears
It is a special case of spiral gears in which angle between the two axes is generally
right angle. The smaller of the two gears is called worm which has large spiral
angle. These are shown in Figure 3.24.
(a) (b)
(c) (d)
Figure 3.24 : Worm Gears
Hypoid Gears
These gears are approximations of hyperboloids though look like spiral bevel
gears. The hypoid pinion is larger and stronger than a spiral bevel pinion. They
have quit and smooth action and have larger number of teeth is contact as
compared to straight bevel gears. These gears are used in final drive of vehicles.
They are shown in Figure 3.25.
Figure 3.25 : Hypoid Gears
1
2

56. 99
Power Transmission
Devices
3.7 GEAR TERMINOLOGY
Before considering kinematics of gears we shall define the terms used for describing the
shape, size and geometry of a gear tooth. The definitions given here are with respect to a
straight spur gear.
Pitch Circle or Pitch Curve
It is the theoretical curve along which the gear rolls without slipping on the
corresponding pitch curve of other gear for transmitting equivalent motion.
Pitch Point
It is the point of contact of two pitch circles.
Pinion
It is the smaller of the two mating gears. It is usually the driving gear.
Rack
It is type of the gear which has infinite pitch circle diameter.
Circular Pitch
It is the distance along the pitch circle circumference between the corresponding
points on the consecutive teeth. It is shown in Figure 3.26.
Figure 3.26 : Gear Terminology
If d is diameter of the pitch circle and ‘T’ be number of teeth, the circular pitch
(pc) is given by
c
d
p
T

 . . . (3.14)
Diamental Pitch
It is defined as the number of teeth per unit pitch circle diameter. Therefore,
diamental pitch (pd) can be expressed as
d
T
p
d
 . . . (3.15)
From Eqs. (3.14) and (3.15)
c
d
d
p
T p
d
 
 
or, c d
p p   . . . (3.16)
Circular Pitch
Top Land
Face
Flank
Addendu
mm
Working
Depth
Clearance
Dedendum
Bottom Land
Dedendum
(Root) Circle
Pitch Circle
Addendum
Circle
Face Width
Space
Width
Tooth
Thicknes
s

57. 100
Theory of Machines Module
It is the ratio of the pitch circle diameter to the number of teeth. Therefore, the
module (m) can be expressed as
d
m
T
 . . . (3.17)
From Eqs. (8.14)
c
p m
  . . . (3.18)
Addendum Circle and Addendum
It is the circle passing through the tips of gear teeth and addendum is the radial
distance between pitch circle and the addendum circle.
Dedendum Circle and Dedendum
It is the circle passing through the roots of the teeth and the dedendum is the radial
distance between root circle and pitch circle.
Full Depth of Teeth and Working Depth
Full depth is sum of addendum and dedendum and working depth is sum of
addendums of the two gears which are in mesh.
Tooth Thickness and Space Width
Tooth thickness is the thickness of tooth measured along the pitch circle and space
width is the space between two consecutive teeth measured along the pitch circle.
They are equal to each other and measure half of circular pitch.
Top Land and Bottom Land
Top land is the top surface of the tooth and the bottom land is the bottom surface
between the adjacent fillets.
Face and Flank
Tooth surface between the pitch surface and the top land is called face whereas
flank is tooth surface between pitch surface and the bottom land.
Pressure Line and Pressure Angle
The driving tooth exerts a force on the driven tooth along the common normal.
This line is called pressure line. The angle between the pressure line and the
common tangent to the pitch circles is known as pressure angle.
Path of Contact
The path of contact is the locus of a point of contact of two mating teeth from the
beginning of engagement to the end of engagement.
Arc of Approach and Arc of Recess
Arc of approach is the locus of a point on the pitch circle from the beginning of
engagement to the pitch point. The arc of recess is the locus of a point from pitch
point upto the end of engagement of two mating gears.
Arc of Contact
It is the locus of a point on the pitch circle from the beginning of engagement to
the end of engagement of two mating gears.
Arc of Contact = Arc of Approach + Arc of Recess
Angle of Action
It is the angle turned by a gear from beginning of engagement to the end of
engagement of a pair of teeth.
Angle of action = Angle turned during arc of approach + Angle turned during arc
of recess

58. 101
Power Transmission
Devices
Contact Ratio
It is equal to the number of teeth in contact and it is the ratio of arc of contact to
the circular pitch. It is also equal to the ratio of angle of action to pitch angle.
Figure 3.27 : Gear Terminology
3.8 GEAR TRAIN
A gear train is combination of gears that is used for transmitting motion from one shaft
to another.
There are several types of gear trains. In some cases, the axes of rotation of the gears are
fixed in space. In one case, gears revolve about axes which are not fixed in space.
3.8.1 Simple Gear Train
In this gear train, there are series of gears which are capable of receiving and
transmitting motion from one gear to another. They may mesh externally or internally.
Each gear rotates about separate axis fixed to the frame. Figure 3.28 shows two gears in
external meshing and internal meshing.
Let t1, t2 be number of teeth on gears 1 and 2.
(a) External Meshing (b) Internal Meshing
Figure 3.28 : Simple Gear Train
B
Dedendum
Circle
Path of
Contact
Drivers
Ψ
Pressure
Angle
Pitch
Circle
Base
Circle
Dedendum
Circle
Angle of
Action
F
P
C
E
A
D
Pitch
Circle
+
1 2
+
1
2
P

59. 102
Theory of Machines Let N1, N2 be speed in rpm for gears 1 and 2. The velocity of P,
1 1 2 2
2 2
60 60
 
 
P
N d N d
V
 1 2 2
2 1 1
 
N d t
N d t
Referring Figure 3.28, the two meshing gears in external meshing rotate in opposite
sense whereas in internal meshing they rotate in same sense. In simple gear train, there
can be more than two gears also as shown in Figure 3.29.
Figure 3.29 : Gear Train
Let N1, N2, N3, . . . be speed in rpm of gears 1, 2, 3, . . . etc., and t1, t2, t3, . . . be number
of teeth of respective gears 1, 2, 3, . . . , etc.
In this gear train, gear 1 is input gear, gear 4 is output gear and gears 2, 3 are
intermediate gears. The gear ratio of the gear train is give by
Gear Ratio 3
1 1 2
4 2 3 4
N
N N N
N N N N
   
3 3
1 2 2 4
2 1 3 2 4 3
; and
t N
N t N t
N t N t N t
  
Therefore, 3
1 2 4 4
4 1 2 3 1
t
N t t t
N t t t t
   
This expression indicates that the intermediate gears have no effect on gear ratio. These
intermediate gears fill the space between input and output gears and have effect on the
sense of rotation of output gear.
SAQ 8
(a) There are six gears meshing externally and input gear is rotating in
clockwise sense. Determine sense of rotation of the output gear.
(b) Determine sense of rotation of output gear in relation to input gear if a
simple gear train has four gears in which gears 2 and 3 mesh internally
whereas other gears have external meshing.
3.8.2 Compound Gear Train
In this type of gear train, at least two gears are mounted on the same shaft and they rotate
at the same speed. This gear train is shown in Figure 3.30 where gears 2 and 3 are
mounted on same shaft and they rotate at the same speed, i.e.
2 3
N N

1
2
3
4

60. 103
Power Transmission
Devices
Figure 3.30 : Compound Gear Train
Let N1, N2, N3, . . . be speed in rpm of gears 1, 2, 3, . . . , etc. and t1, t2, t3, . . . , etc. be
number of teeth of respective gears 1, 2, 3, . . . , etc.
Gear Ratio 3
1 1 2 1
4 2 4 2 4
N
N N N N
N N N N N
    
2 4
1 3
t t
t t
 
Therefore, unlike simple gear train the gear ratio is contributed by all the gears. This
gear train is used in conventional automobile gear box.
Conventional Automobile Gear Box
A conventional gear box of an automobile uses compound gear train. For different
gear engagement, it may use sliding mesh arrangement, constant mesh
arrangement or synchromesh arrangement. Discussion of these arrangements is
beyond the scope of this course. We shall restrict ourselves to the gear train. It can
be explained better with the help of an example.
Example 3.1
A sliding mesh type gear box with four forward speeds has following gear ratios :
Top gear = 1
Third gear = 1.38
Second gear = 2.24
First gear = 4
Determine number of teeth on various gears. The minimum number of teeth on the
pinion should not be less than 18. The gear box should have minimum size and
variation in the ratios should be as small as possible.
Solution
The gears in the gear box are shown in Figure 3.31 below :
Figure 3.31 : Conventional Gear Box
1
2
4
3
A
B
C
E
G
D
F
H
Dog
Clutch
Engine Shaft
Input Shaft
Main Splined
Shaft
(Output Shaft)
Lay
Shaft

61. 104
Theory of Machines For providing first gear ratio, gear A meshes with gear B and gear H meshes with
gear G.
Speed of engine shaft
First gear ratio =
Speed of output shaft
A A H A H
G H G B G
N N N N N
N N N N N
    
[i.e. NB = NH]
G
B
A H
t
t
t t
 
For smallest size of gear box G
B
A H
t
t
t t
 
 4.0 2.0
G
B
A H
t
t
t t
  
If tA = 20 teeth  tH = 20
 tB = 2  20 = 40 teeth and tG = 20  2 = 40 teeth
Since centre distance should be same
 A B C D E F H G
t t t t t t t t
      
40 20 60
C D
t t
    . . . (3.19)
60
E F
t t
  . . . (3.20)
For second gear, gear A meshes with gear B and gear E meshes with gear F.
 2.24
A
G
N
N

or, 2.24
A F
B E
N N
N N
 
 2.24
B E
A F
t t
t t
 
or, 2 2.24
F
G
t
t
 
or,
2.24
1.12
2
E
F
t
t
  . . . (3.21)
From Eqs. (10.2) and (10.3)
1.12 60
F F
t t
 
or,
60
28.3 60
2.12
F E F
t t t
    
or, 60 28.3 31.7
E
t   
Since number of teeth have to be in full number. Therefore, tF can be either 28 or
29 and tE can be either 31 or 32. If tF = 28 and tE = 32.
Second gear ratio
40 32
2.286
20 28
A E
B F
t t
t t
    

62. 105
Power Transmission
Devices
If tF = 29 and tE = 31.
Second gear ratio
40 31
2.138
20 29
  
From these two values of gear ratios, 2.286 is closer to 2.24 than 2.138.
For third gear, gear A meshes with gear B and gear D meshes with gear C.
 1.38
A
C
N
N

or, 1.38
A D
B C
N N
N N
 
or, 1.38
C
B
A D
t
t
t t
 
or,
40
1.38
20
C
D
t
t
 
2 1.38
C
D
t
t
 
or,
1.38
0.69
2
C
D
t
t
  . . . (3.22)
From Eqs. (3.19) and (3.20)
tC = 0.69 tD
tD + 0.69 tD = 60
or,
60
35.503
1.69
 
D
t
 60 60.35.503 24.497
   
C D
t t
Either tC = 24 and tD = 36 or tC = 25 and tD = 35.
If tC = 25 and tD = 35.
Third gear ratio
40 25
1.4286
20 35
    
C
B
A D
t
t
t t
If tC = 24 and tD = 36
Third gear ratio
40 24
1.333
20 36
  
Since 1.333 is closer to 1.38 as compared to 1.4286.
Therefore, tC = 24 and tD = 36
The top gear requires direct connection between input shaft and output shaft.
3.8.3 Power Transmitted by Simple Spur Gear
When power is bring transmitted by a spur gear, tooth load Fn acts normal to the profile.
It can be resolved into two components Fn cos  and Fn sin . Fn cos  acts tangentially
to the pitch circle and it is responsible for transmission of power
 Power transmitted (P) = Fn cos  . V
where V is pitch line velocity.

63. 106
Theory of Machines
Since
2
60 2

 
N tm
V

2
cos
60 2

   
n
N tm
P F
where t is number of teeth and m is module.
Figure 3.32
Example 3.2
An open flat belt drive is required to transmit 20 kW. The diameter of one of the
pulleys is 150 cm having speed equal to 300 rpm. The minimum angle of contact
may be taken as 170o
. The permissible stress in the belt may be taken as
300 N/cm2
. The coefficient of friction between belt and pulley surface is 0.3.
Determine
(a) width of the belt neglecting effect of centrifugal tension for belt
thickness equal to 8 mm.
(b) width of belt considering the effect of centrifugal tension for the
thickness equal to that in (a). The density of the belt material
is 1.0 gm/cm3
.
Solution
Given that Power transmitted (p) = 20 kW
Diameter of pulley (d) = 150 cm = 1.5 m
Speed of the belt (N) = 300 rpm
Angle of lap () o 170
170 2.387 radian
180
   
Coefficient of friction () = 0.3
Permissible stress () = 300 N/cm2
(a) Thickness of the belt (t) = 8 mm = 0.8 cm
Let higher tension be ‘T1’ and lower tension be ‘T2’.
 0.3 2.387
1
2
2.53
T
e e
T
 
  
The maximum tension ‘T1’ is controlled by the permissible stress.
Fn
Pressure
angle 

64. 107
Power Transmission
Devices
1 300 0.8 24 N
10
b
T b t b
     
Here b is in mm
Therefore, 1
2
24
N
2.53 2.53
T b
T  
Velocity of belt
2 2 300 1.5
23.5 m/s
60 2 60 2
N d
V
  
    
 Power transmitted 1 2
24 23.5
( ) 24 kW
2.53 1000
b
p T T V b
 
    
 
 
1 23.5 347.3
24 1
2.53 1000 1000
b
b
 
   
 
 
Since P = 20 kW

347.3
20
1000
b

or,
20 1000
36.4 mm
347.3
b

 
(b) The density of the belt material  = 1 gm/cm3
Mass of the belt material/length, m =  b t  1 metre
2
1
0.8 100 0.8 10 kg/m
1000 10

     
b
b
3
8 10 kg/m
b 
 
 Centrifugal tension ‘TC’ = m V2
or, 3 2
8 10 (23.5) = 4.418 N
C
T b b

  
Maximum tension (Tmax) = 24b N
 1 max 24 4.418 19.58
C
T T T b b b
    
Power transmitted 1
1
1
P T V
e
 
 
 
 
1 23.5 460.177
19.58 1
2.53 1000 1000
b
b
 
   
 
 
Also P = 20 kW

460.177
20
1000
b

or, b = 45.4 mm
The effect of the centrifugal tension increases the width of the belt required.
Example 3.3
An open belt drive is required to transmit 15 kW from a motor running at 740 rpm.
The diameter of the motor pulley is 30 cm. The driven pulley runs at 300 rpm and
is mounted on a shaft which is 3 metres away from the driving shaft. Density of
the leather belt is 0.1 gm/cm3
. Allowable stress for the belt material is 250 N/cm2
.
If coefficient of friction between the belt and pulley is 0.3, determine width of the
belt required. The thickness of the belt is 9.75 mm.

65. 108
Theory of Machines Solution
Given data :
Power transmitted (P) = 15 kW
Speed of motor pulley (N1) = 740 rpm
Diameter of motor pulley (d1) = 30 cm
Speed of driven pulley (N2) = 300 rpm
Distance between shaft axes (C) = 3 m
Density of the belt material () = 0.1 gm/cm3
Allowable stress () = 250 N/cm2
Coefficient of friction () = 0.3
Let the diameter of the driven pulley be ‘d2’
 N1 d1 = N2 d2
 1 1
2
2
740 30
74 cm
300
N d
d
N

  
1
2 1 74 30
sin sin
2 2 300
d d
C

 
    

or,  = 0.0734 radian
2 2.94 rad
     
Mass of belt ‘m’ =  b t  one metre length
0.1 9.75
100
1000 10 10
b
   
where ‘b’ is width of the belt in ‘mm’
or, 3
0.975 10 kg/m
m b

 
max
9.75
250 24.375 N
10 10
b
T b
   
Active tension ‘T’ = Tmax – TC
Velocity of belt 1 1
2
60 2
N d
V


740 30
60 100
 
 
or, V = 11.62 m/s
2 3 2
0.975 10 (11.62)
C
T m V b

   
= 0.132 b N
 1 24.375 0.132 24.243
T b b b
  
Power transmitted 1
1
1
P T V
e
 
 
 
 

66. 109
Power Transmission
Devices
0.3 2.94
2.47
e e
 
 
1 11.62 165
24.243 1
2.47 1000 1000
b
P
 
   
 
 

165
15 or 91 mm
100
b
b
 
Example 3.4
An open belt drive has two pulleys having diameters 1.2 m and 0.5 m. The pulley
shafts are parallel to each other with axes 4 m apart. The mass of the belt is 1 kg
per metre length. The tension is not allowed to exceed 2000 N. The larger pulley
is driving pulley and it rotates at 200 rpm. Speed of the driven pulley is 450 rpm
due to the belt slip. The coefficient of the friction is 0.3. Determine
(a) power transmitted,
(b) power lost in friction, and
(c) efficiency of the drive.
Solution
Data given :
Diameter of driver pulley (d1) = 1.2 m
Diameter of driven pulley (d2) = 0.5 m
Centre distance (C) = 4 m
Mass of belt (m) = 1 kg/m
Maximum tension (Tmax) = 2000 N
Speed of driver pulley (N1) = 200 rpm
Speed of driven pulley (N2) = 450 rpm
Coefficient of friction () = 0.3
(a) 1
1
2 2 200
20.93 r/s
60 60
N
  
   
2
2
2 2 450
47.1 r/s
60 60
N
 
   
Velocity of the belt (V)
1.2
20.93 12.56 m/s
2
  
Centrifugal tension (TC) = m V2
= 1  (12.56)2
= 157.75 N
Active tension on tight side (T1) = Tmax – TC
or, T1 = 2000 – 157.75 = 1842.25 N
1 2 1.2 0.5
sin 0.0875
2 2 4
d d
C
 
   

or,  = 5.015o
o
180 2 180 2 5.015 169.985
       
or,
169.985
0.3
1 180
2
2.43
T
e e
T


  

67. 110
Theory of Machines
Power transmitted 1
1
( ) 1 12.56
2.43
P T
 
  
 
 
1 12.56
1842.25 1 kW
2.43 1000
 
 
 
 
= 13.67 kW
(b) Power output 2 2
1
1
1 W
2.43 2

 
  
 
 
d
T
1 47.1 0.5
1842.25 1 12.2 kW
2.43 2 1000

 
   
 

 
 Power lost in friction = 13.67 – 12.2 = 1.47 kW
(c) Efficiency of the drive
Power transmitted 12.2
0.89 or 89%
Power input 13.67
   .
Example 3.5
A leather belt is mounted on two pulleys. The larger pulley has diameter equal to
1.2 m and rotates at speed equal to 25 rad/s. The angle of lap is 150o
. The
maximum permissible tension in the belt is 1200 N. The coefficient of friction
between the belt and pulley is 0.25. Determine the maximum power which can be
transmitted by the belt if initial tension in the belt lies between 800 N and 960 N.
Solution
Given data :
Diameter of larger pulley (d1) = 1.2 m
Speed of larger pulley 1 = 25 rad/s
Speed of smaller pulley 2 = 50 rad/s
Angle of lap () = 150o
Initial tension (T0) = 800 to 960 N
Let the effect of centrifugal tension be negligible.
The maximum tension (T1) = 1200 N
150
0.25
1 180
2
1.924
T
e e
T
  

  
1
2
1200
623.6 N
1.924 1.924
T
T   
1 2
0
1200 623.6
911.8 N
2 2
T T
T
 
  
Maximum power transmitted (Pmax) = (T1 – T2) V
Velocity of belt (V) 1
1
1.2
25
2 2
d
   
V = 15 m/s
 max (1200 623.6) (1200 623.6) 15
P V
   
8646 W or 8.646 kW


68. 111
Power Transmission
Devices
Example 3.6
A shaft carries pulley of 100 cm diameter which rotates at 500 rpm. The ropes
drive another pulley with a speed reduction of 2 : 1. The drive transmits 190 kW.
The groove angle is 40o
. The distance between pulley centers is 2.0 m. The
coefficient of friction between ropes and pulley is 0.20. The rope weighs
0.12 kg/m. The allowable stress for the rope is 175 N/cm2
. The initial tension in
the rope is limited to 800 N. Determine :
(a) number of ropes and rope diameter, and
(b) length of each rope.
Solution
Given data :
Diameter of driving pulley (d1) = 100 cm = 1 m
Speed of the driving pulley (N1) = 500 rpm
Speed of the driven pulley (N2) = 250 rpm
Power transmitted (P) = 190 kW
Groove angle () = 40o
Centre distance (C) = 2 m
Coefficient of friction () = 0.2
Mass of rope = 0.12 kg/m
Allowable stress () = 175 N/cm2
Initial tension (T0) = 800 N
The velocity of rope 1 1 1 500
26.18 m/s
60 60
d N
   
  
Centrifugal tension (TC) = 0.12 (26.18)2
= 82.25 N
2 1
( ) 2 1
sin 0.25
2 2 2
 
   

d d
C
or,  = sin 0.25– 1
= 14.18
 Angle of lap () =   2 = 151o
or 2.636 radian

o
0.2 2.636
sin 20
1
2
4.67
T
e
T

 
or, T1 = 4.67 T2
Initial tension (T0) 1 2 2
800
2
C
T T T
 
 
 1 2 1600 2 82.25 1600 164.5 1435.5 N
T T
      
 2 2
4.67 1435.5
T T
 
or, T2 = 253.1 N
 T1 = 4.67 T2 = 1182.0 N
 1 2
26.18
( ) (1182.0 253.1) 24.32 kW
1000 1000
V
P T T
     
Numbers of ropes required (n)
190
7.81
24.32
  or say 8 ropes,

69. 112
Theory of Machines Maximum tension (Tmax) = T1 + TC
= 1182 + 82.25 = 1264.25 N
2
max 1264.25
4
T d

  
or, 2 1264.25 4
9.2
175
d

 
 
or, d = 3.03 cm
This is open belt drive, therefore, formula for length of rope is given by
2
2
( ) 1
( ) 2 1
2
R r R r
L R r C
C C
 
 
 
     
 
 
 
 
 
2 1
2 1
1 m, 0.5 m
2 2 2 2
d d
R r
     

2
2
(1 0.5) 1 1 0.5
(1 0.5) 2 2 1
2 2 2
L
 
 
 
      
 
 
 
 
 
0.25
1.5 4 (1 0.5 0.0625) 8.72 m
2
       .
3.9 SUMMARY
The power transmission devices are belt drive, chain drive and gear drive. The belt drive
is used when distance between the shaft axes is large and there is no effect of slip on
power transmission. Chain drive is used for intermediate distance. Gear drive is used for
short centre distance. The gear drive and chain drive are positive drives but they are
comparatively costlier than belt drive.
Similarly, belt drive should satisfy law of belting otherwise it will slip to the side and
drive cannot be performed. When belt drive transmits power, one side will become tight
side and other side will become loose side. The ratio of tension depends on the angle of
lap and coefficient of friction. If coefficient of friction is same on both the pulleys
smaller angle of lap will be used in the formula. If coefficient of friction is different, the
minimum value of product of coefficient of friction and angle of lap will decide the ratio
of tension, i.e. power transmitted. Due to the mass of belt, centrifugal tension acts and
reduces power transmitted. For a given belt drive the power transmitted will be
maximum at a speed for which centrifugal tension is one third of maximum possible
tension.
The gears can be classified according to the layout of their shafts. For parallel shafts spur
or helical gears are used and bevel gears are uded for intersecting shafts. For skew shafts
when angle between the axes is 90o
worm and worm gears are used. When distance
between the axes of shaft is larger and positive drive is required, chain drive is used. We
can see the use of chain drive in case of tanks, motorcycles, etc.
3.10 KEY WORDS
Spur Gears : They have straight teeth with teeth layout is
parallel to the axis of shaft.
Helical Gears : They have curved or straight teeth and its
inclination with shaft axis is called helix angle.

70. 113
Power Transmission
Devices
Herringbone Gears : It is a double helical gear having left and right
inclinations which meet at a common apex and
there is no groove in between them.
Bevel Gear : They have teeth radial to the point of intersection
of the shaft axes and they vary in cross-section
throughout their length.
Spiral Gears : They have curved teeth which are inclined to the
shaft axis. They are used for skew shafts.
Worm Gears : It is special case of spiral gears where angle
between axes of skew shafts is 90o
.
Rack and Pinion : Rack is special case of a spur gear whose pitch
circle diameter is infinite and it meshes with a
pinion.
Hypoid Gears : These gears are approximations of hyperboloids
but they look like spiral gears.
Pitch Cylinders : A pair of gears in mesh can be replaced by a pair
of imaginary friction cylinders which by pure
rolling motion transmit the same motion as pair of
gears.
Pitch Diameter : It is diameter of pitch cylinders.
Circular Pitch : It is the distance between corresponding points of
the consecutive teeth along pitch cylinder.
Diametral Pitch : It is the ratio of number of teeth to the diameter of
the pitch cylinders.
Module : It is the ratio of diameter of pitch cylinder to the
number of teeth.
Addendum : It is the radial height of tooth above pitch cylinder.
Dedendum : It is the radial depth of tooth below pitch cylinder.
Pressure Angle : It is the angle between common tangent to the two
pitch cylinders and common normal at the point of
contact between teeth (pressure line).
3.11 ANSWERS TO SAQs
SAQ 1
Available in text.
SAQ 2
(a) Available in text.
(b) Available in text.
SAQ 3
(a) Available in text.
(b) Data given :
Speed of prime mover (N1) = 300 rpm
Speed of generator (N2) = 500 rpm
Diameter of driver pulley (d1) = 600 mm
Slip in the drive (s) = 3%
Thickness of belt (t) = 6 mm

71. 114
Theory of Machines
If there is no slip 2 1
1 2
N d
N d
 .
If thickness of belt is appreciable and no slip
2 1
1 2
N d t
N d t



If thickness of belt is appreciable and slip is ‘S’ in the drive
2 1
1 2
1
100
N d t S
N d t
  
 
 
  

2
500 600 6 3
1
300 100
d t
  
 
 
  
or, 2
606
( 6) 300 0.97 352.692
500
d     
or, 2 352.692 6 346.692 mm
d   
SAQ 4
Available in text.
SAQ 5
Available in text.
SAQ 6
Available in text.
SAQ 7
Available in text.
SAQ 8
Available in text.

72. Types of Gears
• Spur gears have teeth parallel to the axis of rotation and are used to
transmit motion from one shaft to another, parallel, shaft.
• Helical gears have teeth inclined to the axis of rotation. Helical gears
are not as noisy, because of the more gradual engagement of the
teeth during meshing.
• Bevel gears have teeth formed on conical surfaces and are used
mostly for transmitting motion between intersecting shafts.
• Worms and worm gears ,The worm resembles a screw. The
direction of rotation of the worm gear, also called the worm wheel,
depends upon the direction of rotation of the worm and upon
whether the worm teeth are cut right-hand or left-hand.
3

73. SPUR GEAR
SPUR GEAR
• Teeth is parallel to axis of rotation
p
• Transmit power from one shaft to
another parallel shaft
U d i El t i d i
• Used in Electric screwdriver,
oscillating sprinkler, windup alarm
clock, washing machine and clothes
dryer
y

74. External and Internal spur Gear…
External and Internal spur Gear…
• Advantages:
Economical
– Economical
– Simple design
– Ease of maintenance
Ease of maintenance
• Disadvantages:
– Less load capacity
p y
– Higher noise levels

75. Helical Gear
• The teeth on helical gears are cut at an angle to the face of the gear
• This gradual engagement makes helical gears operate much more
This gradual engagement makes helical gears operate much more
smoothly and quietly than spur gears
• Carry more load than equivalent-sized spur gears
6

76. Helical Gear…
Helical Gear…

77. Herringbone gears
Herringbone gears
• To avoid axial thrust, two
,
helical gears of opposite
hand can be mounted side
b side to cancel res lting
by side, to cancel resulting
thrust forces
• Herringbone gears are
mostly used on heavy
mostly used on heavy
machinery.

78. Rack and pinion
Rack and pinion
• Rack and pinion gears are used to
convert rotation (From the pinion) into
linear motion (of the rack)
• A perfect example of this is the steering
system on many cars

79. Bevel gears
• Bevel gears are useful when the direction of a shaft's
i d b h d
rotation needs to be changed
• They are usually mounted on shafts that are 90
degrees apart b t can be designed to ork at other
degrees apart, but can be designed to work at other
angles as well
• The teeth on bevel gears can be straight spiral or
• The teeth on bevel gears can be straight, spiral or
hypoid
• locomotives marine applications automobiles
locomotives, marine applications, automobiles,
printing presses, cooling towers, power plants, steel
plants, railway track inspection machines, etc.
10

80. Straight and Spiral Bevel Gears
Straight and Spiral Bevel Gears

81. WORM AND WORM GEAR
• Worm gears are used when large gear reductions are
g g g
needed. It is common for worm gears to have
reductions of 20:1, and even up to 300:1 or greater
• Many worm gears have an interesting property that
no other gear set has: the worm can easily turn the
gear but the gear cannot turn the worm
gear, but the gear cannot turn the worm
• Worm gears are used widely in material handling
and transportation machinery machine tools
and transportation machinery, machine tools,
automobiles etc
12

82. WORM AND WORM GEAR
13

83. Nomenclature
9 The pitch circle is a theoretical circle upon which all calculations are usually
based; its diameter is the pitch diameter.
9 A pinion is the smaller of two mating gears. The larger is often called the
p g g g
gear.
9 The circular pitch p is the distance, measured on the pitch circle, from a
point on one tooth to a corresponding point on an adjacent tooth. It is
equalto the sum of the tooth thickness and width of space.
9 The module m is the ratio of the pitch diameter to the number of teeth.
9 The diametral pitch P is the ratio of the number of teeth on the gear to the
pitch diameter.
14

84. Nomenclature
9 The addendum a is the radial distance between the top land and the pitch
circle (1m).
9 The dedendum b is the radial distance from the bottom land to the pitch
p
circle (1.25m). The whole depth ht is the sum of the addendum and the
dedendum.
9 The clearance circle is a circle that is tangent to the addendum circle of the
mating gear.
9 The clearance c is the amount by which the dedendum in a given gear
exceeds the addendum of its mating gear.
9 The backlash is the amount by which the width of a tooth space exceeds the
thickness of the engaging tooth measured on the pitch circles
thickness of the engaging tooth measured on the pitch circles.
15

85. Conjugate Action
• Tooth profiles are designed so as to produce a
constant angular velocity ratio during meshing,
conjugate action.
j g
• When one curved surface pushes against
another ,the point of contact occurs where the two
surfaces are tangent to each other (point c), and
the forces at any instant are directed along the
the forces at any instant are directed along the
common normal ab (line of action) to the two
curves.
• The angular-velocity ratio between the two arms is
The angular velocity ratio between the two arms is
inversely proportional to their radii to the point P.
• Circles drawn through point P are called pitch
circles, and point P is called the pitch point.
Mating
gear teeth
produce
rotary
• To transmit motion at a constant angular-velocity
ratio, the pitch point must remain fixed; that is, all
the lines of action for every instantaneous point of
contact must pass through the same point P
rotary
motion
similar to
cams
16
contact must pass through the same point P.

86. VELOCITY RATIO OF GEAR DRIVE
• In the case of involute profiles, all points of contact occur on the same
straight line ab. All normal to the tooth profiles at the point of contact
coincide with the line ab thus these profiles transmit uniform rotary
coincide with the line ab, thus these profiles transmit uniform rotary
motion.
• When two gears are in mesh their pitch circles roll on one another without
slippage Then the pitch line velocity is V= r ω = r ω
slippage. Then the pitch line velocity is V= r1ω1 = r2 ω2
d = Diameter of the wheel
d
N
ω
N =Speed of the wheel
ω = Angular speed
velocity ratio (n) =
2
1
1
2
1
2
d
d
N
N
=
=
ω
ω
17

87. Involute Properties ( read)
• An involute curve may be generated with a
partial flange B attached to the cylinder A,
around which wrapped a cord def held tight.
pp g
• Point b on the cord represents the tracing
point, and as the cord is wrapped and
unwrapped about the cylinder, point b will
trace out the involute curve ac
trace out the involute curve ac.
• The generating line de is normal to the
involute at all points of intersection and, at
the same time is always tangent to the
the same time, is always tangent to the
cylinder.
• The point of contact moves along the
generating line; the generating line does not
h iti b it i l t t
change position, because it is always tangent
to the base circles; and since the generating
line is always normal to the involutes at the
point of contact, the requirement for uniform
ti i ti fi d
18
motion is satisfied.

88. Base pitch relation to circular pitch
r: radius of the pitch circle
Base pitch relation to circular pitch

89. Fundamentals
• When two gears are in mesh, their pitch circles roll on one
another without slipping. The pitch-line velocity is
• Thus the relation between the radii on the angular velocities
Thus the relation between the radii on the angular velocities
is
• The addendum and dedendum distances for standard
interchangeable teeth are 1/P and 1 25/P respectively
interchangeable teeth are, 1/P and 1.25/P, respectively.
• The pressure line (line of action)
represent the direction in which the
resultant force acts between the gears.
• The angle φ is called the pressure angle
and it usually has values of 20o or 25o
and it usually has values of 20 or 25
• The involute begins at the base circle and is
undefined below this circle.
20

90. Fundamentals
• If we construct tooth profiles through point a and draw radial lines from the
intersections of these profiles with the pitch circles to the gear centers, we obtain
the angle of approach for each gear.
• The final point of contact will be where the addendum circle of the driver crosses
the pressure line The angle of recess for each gear is obtained in a manner
the pressure line. The angle of recess for each gear is obtained in a manner
similar to that of finding the angles of approach.
• We may imagine a rack as a spur gear having an infinitely large pitch diameter.
Therefore, the rack has an infinite number of teeth and a base circle which is an
i fi it di t f th it h i t
21
infinite distance from the pitch point.

91. Contact Ratio
• The zone of action of meshing gear teeth is shown with the distance AP being the arc
of approach qa , and the distance P B being the arc of recess qr .
• Tooth contact begins and ends at the intersection of the two addendum circles with
• Tooth contact begins and ends at the intersection of the two addendum circles with
the pressure line.
• When a tooth is just beginning contact at a, the previous tooth is simultaneously
ending its contact at b for cases when one tooth and its space occupying the entire
AB
arc AB.
• Because of the nature of this tooth action, either
one or two pairs of teeth in contact, it is
convenient to define the term contact ratio mc as
a number that indicates the average number of pairs of teeth in contact.
a number that indicates the average number of pairs of teeth in contact.
•Gears should not generally be designed having contact ratios less than about 1.20,
because inaccuracies in mounting might reduce the contact ratio even more,
increasing the possibility of impact between the teeth as well as an increase in the
noise level
22
noise level.

92. Interference
• The contact of portions of tooth
profiles that are not conjugate is
called interference.
• When the points of tangency of the
pressure line with the base circles C
and D are located inside of points A
and B ( initial and final points of
and B ( initial and final points of
contact), interference is present.
• The actual effect of interference is
that the involute tip or face of the
that the involute tip or face of the
driven gear tends to dig out the
noninvolute flank of the driver.
• When gear teeth are produced by a
ti i t f i
generation process, interference is
automatically eliminated because the
cutting tool removes the interfering
portion of the flank. This effect is
ll d d tti
23
called undercutting.

93. Interference Analysis
• The smallest number of teeth on a spur pinion and gear, one-to-one
gear ratio, which can exist without interference is NP .
• The number of teeth for spur gears is given by
h k 1 f f ll d th t th 0 8 f t b t th d l
where k = 1 for full-depth teeth, 0.8 for stub teeth and φ = pressure angle.
• If the mating gear has more teeth than the pinion, that is, mG =
NG/NP = m is more than one, then the smallest number of teeth on
the pinion without interference is given by
the pinion without interference is given by
• The largest gear with a specified pinion that is interference-free is
g g p p
• The smallest spur pinion that will operate with a rack without
i t f i
24
interference is

96. The Forming of Gear Teeth ( read)
• There are a large number of ways of forming the teeth of gears,
such as sand casting, shell molding, investment casting, permanent-
mold casting die casting centrifugal casting powder-metallurgy
mold casting, die casting, centrifugal casting, powder-metallurgy
process, extrusion.
• The teeth may be finished, after cutting, by either shaving or
burnishing Several shaving machines are available that cut off a
burnishing. Several shaving machines are available that cut off a
minute amount of metal, bringing the accuracy of the tooth profile
within the limits of 250 μin.
27

97. Straight Bevel Gears (read)
• When gears are used to transmit motion between intersecting shafts,
some form of bevel gear is required.
• The terminology of bevel gears is illustrated.
• The pitch angles are defined by the pitch cones meeting at the apex,
as shown in the figure. They are related to the tooth numbers as
follows:
where the subscripts P and G refer to the pinion and
gear, respectively, and where γ and Г are,
respectively, the pitch angles of the pinion and gear.
Standard straight tooth bevel gears are cut by using a
20o pressure angle and full depth teeth. This
increases contact ratio, avoids undercut, and
increases the strength of the pinion.
28
increases the strength of the pinion.

98. Parallel Helical Gears
• Helical gears subject the shaft bearings to
both radial and thrust loads. When the thrust
load become high it maybe desirable to use
load become high it maybe desirable to use
double helical gears (herringbone) which is
equivalent to helical gears of opposite hand,
mounted side by side on the same shaft.
mounted side by side on the same shaft.
They develop opposite thrust reactions and
thus cancel out.
• When two or more single helical gears are
mounted on the same shaft. The hand of the
gears should be selected to minimize the
gears should be selected to minimize the
thrust load.
29

99. Parallel Helical Gears
• The shape of the tooth of Helical gears is an involute
helicoid.
The initial contact of helical gear teeth is a point that
• The initial contact of helical-gear teeth is a point that
extends into a line as the teeth come into more
engagement. In spur gears the line of contact is
parallel to the axis of rotation; in helical gears the line
is diagonal across the face of the tooth
is diagonal across the face of the tooth.
• The distance ae is the normal circular pitch pn and is
related to the transverse circular pitch as follows:
• The distance ad is called the axial pitch px and is
related by the expression
• The normal diametral pitch Pn
• Normal circular pitch x normal diametral pitch (pnxPn=π)
Transverse diametral pitch
30
• The pressure angle φn in the normal direction is
different from the pressure angle φt in the direction of
rotation. These angles are related by the equation

100. Parallel Helical Gears (Cont.)
• The pressure angle φt in the tangential (rotation) direction is
• The smallest tooth number NP of a helical-spur pinion that will run
without interference with a gear with the same number of teeth is
without interference with a gear with the same number of teeth is
• The largest gear with a specified pinion is given by
• The smallest pinion that can be run with a rack is
31

103. Worm Gears (read)
• The worm and worm gear of a set have the same hand of helix as for
crossed helical gears.
• It is usual to specify the lead angle λ on the worm and helix angle ψG
on the gear; the two angles are equal for a 90◦
shaft angle.
• Since it is not related to the number of teeth, the worm may have any
pitch diameter; this diameter should, however, be the same as the
pitch diameter of the hob used to cut the worm-gear teeth. Generally,
where C is the center distance.
•The lead L and the lead angle λ of the worm
have the following relations:
34

104. Tooth Systems Spur gears
• A tooth system is a standard
that specifies the
relationships involving
p g
addendum, dedendum,
working depth, tooth
thickness, and pressure
angle.
g
• Tooth forms for worm
gearing have not been highly
standardized, perhaps
because there has been less
because there has been less
need for it.
• The face width FG of the
worm gear should be made Worm gears
worm gear should be made
equal to the length of a
tangent to the worm pitch
circle between its points of
intersection with the
Worm gears
35
intersection with the
addendum circle.

105. Standard Tooth Properties
Helical gears
Bevel gears
36

110. Gear Trains
• Consider a pinion 2 driving a gear 3. The speed of the
driven gear is
where n = revolutions or rev/min N = number of teeth
d = pitch diameter
• Gear 3 is an idler that affects only the direction of
rotation of gear 6.
• Gears 2, 3, and 5 are drivers, while 3, 4, and 6 are
dri en members We define the train al e e as
driven members. We define the train value e as
• As a rough guideline, a train value of up to 10 to 1 can
g g p
be obtained with one pair of gears. A two-stage
compound gear train can obtain a train value of up to
100 to 1.
It i ti d i bl f th i t h ft d th
41
• It is sometimes desirable for the input shaft and the
output shaft of a two-stage compound gear train to be
in-line.

113. Planetary Gear Train
• Planetary trains always include a sun gear, a
planet carrier or arm, and one or more planet
gears.
g
• The figure shows a planetary train composed of a
sun gear 2, an arm or carrier 3, and planet gears
4 and 5.
• The angular velocity of gear 2 relative to the arm
in rev/min is
• The ratio of gear 5 to that of gear 2 is the same
• The ratio of gear 5 to that of gear 2 is the same
and is proportional to the tooth numbers, whether
the arm is rotating or not. It is the train value.
or
44

119. Force Analysis : Spur Gearing
• Free-body diagrams of the forces and moments acting upon two
gears of a simple gear train are shown.
Th H t itt d th h t ti b
• The power H transmitted through a rotating gear can be
obtained from the standard relationship of the product of torque
T and angular velocity .
• Gear data is often tabulated using pitch-line velocity, V = (d/2) ω.
where
V =pitch-line velocity ft/min;d =gear diameter,in;n =gear speed, rev/min
• With the pitch-line velocity and appropriate conversion factors
incorporated, Eq. (13–33) can be rearranged and expressed in
c stomar nits as
customary units as
where Wt =transmitted load, lbf; H =power,hp;V =pitch-line velocity,ft/min
50

121. Force Analysis : Bevel Gearing (read)
• In determining shaft and bearing loads for bevel-gear applications,
the usual practice is to use the tangential or transmitted load that
would occur if all the forces were concentrated at the midpoint of the
would occur if all the forces were concentrated at the midpoint of the
tooth.
• The transmitted load
where T is the torque and rav is the pitch radius at the midpoint of the
tooth for the gear under consideration
tooth for the gear under consideration.
• The forces acting at the center of the tooth are shown
52

122. Force Analysis : Helical Gearing
• A three-dimensional view of the forces acting against a helical-
gear tooth is shown.
• The three components of the total (normal) tooth force W are
where W = total force
W di l t
Wr = radial component
Wt = tangential component,
also called transmitted load
W a ial component
Wa = axial component,
also called thrust load
53

123. Force Analysis : Worm Gearing (read)
• If friction is neglected, then the only force exerted by the gear will be
the force W as shown.
• Since the gear forces are opposite to the worm forces
• By introducing a coefficient of friction f
• Efficiency η can be defined by using the equation
when
After some rearranging
• Many experiments have shown that the coefficient of friction is
d d t th l ti lidi l it
54
dependent on the relative or sliding velocity.

130. At the end of this video, you should be able to:
• Explain what a cam is, how it is used, and the typical types of cams
• Identify force closed and form closed followers and explain the
benefits and limitations of each
• Describe the primary types of cam motion programs
Introduction to Cam Design
Source: Norton, Design of Machinery

131. What is a Cam and Follower?
Cam: specially shaped part designed to move a follower
in a controlled fashion
Follower: a link constrained to rotate or translate
• A cam‐follower is a degenerate 4‐bar linkage
Source: Norton, Design of Machinery

132. What are Cams Used For?
• Valve actuation in IC engines
• Motion control in machinery
• Force generation
• Precise positioning
• Event timing

133. Overhead Valve Overhead Camshaft
Valve Trains
Source: Norton, Cam Design and
Manufacturing Handbook

134. Industrial Cam Trains
Source: Norton, Cam Design and
Manufacturing Handbook

135. Hydraulic Pump Application

136. Stationary
segment
Stationary-axial-track
Radial or plate
Barrel or axial - track
Radial or plate
Radial
track
Types of Cams
Source: Norton, Cam Design and
Manufacturing Handbook

137. Types of Followers
Source: Norton,
Design of Machinery

138. Force Closed:
Two Ways to Close Follower Joint
Form Closed:
Source: Norton,
Design of Machinery

139. Conjugate Cams
Source: Norton,
Design of Machinery

140. Barrel Cams
Tracked:
z
FIGURE 13-13
Ribbed barrel cam with oscillating roller follower
Ribbed:
Source: Norton,
Design of Machinery

141. Rotary Indexers Use Ribbed Barrel Cams

142. Types of Cam Motion Programs
• No‐Dwell or Rise‐Fall (RF)
• Single‐Dwell or Rise‐Fall‐Dwell (RFD)
• Double‐Dwell (RDFD)
• Multi‐Rise‐Multi‐Dwell‐Multi‐Fall
• Different Motion Programs Needed for Each

143. A Cam Timing Diagram
FIGURE 2-2
A cam timing diagram
1
0
Motion
mm or in
Low
dwell
High
dwell
Rise Fall
1.0
0.25 0.50 0.75
0 Time t sec
90 180 270 360
0 Cam angle θ deg

144. SVAJ Diagrams
S
V
A
J

146. At the end of this video, you should be able to:
• Describe the difference between critical extreme position and
critical path motion
• Explain how the fundamental law of cam design applies to selecting
an appropriate cam profile
• Design double dwell cam profiles using a variety of motion types
Cam Motion Design: Critical Extreme Position
Source: Norton, Design of Machinery

147. Unwrapping Cam Profile
θ
S - Position
Source: Norton, Design of Machinery

148. Type of Motion Constraints
• Critical Extreme Position (CEP)
– End points of motion are critical
– Path between endpoints is not critical
• Critical Path Motion (CPM)
– The path between endpoints is critical
– Displacements, velocities, etc. may be specified
– Endpoints usually also critical

149. Double Dwell Cam Timing Diagram
FIGURE 2-2
A cam timing diagram
1
0
Motion
mm or in
Low
dwell
High
dwell
Rise Fall
1.0
0.25 0.50 0.75
0 Time t sec
90 180 270 360
0 Cam angle θ deg

150. Naïve and Poor Cam Design: Constant Velocity
FIGURE 2-3
The s v a j diagrams of a "bad" cam design—pure constant velocity
h
0
s
v
0
90 180 270 360
0
a
0
j
0
∞ ∞
∞
∞
Low
dwell
High
dwell
Rise Fall
deg
θ
deg
θ
deg
θ
deg
θ
∞ 2
(a)
(b)
(c)
(d )
∞ 2
∞ 2
∞ 2

151. Constant Acceleration (Parabolic Displacement)?
FIGURE 2-6
Constant acceleration gives infinite jerk
(a) Acceleration
(b) Jerk
Low
dwell
High
dwell
Rise
a
0
j
∞
∞
∞
θ
θ
max
a
min
a
0
0 β
0 β

152. Simple Harmonic Motion (SHM)?
s
h
v
h
a
h
j
h
= (2.6a)
= (2.6b)
= (2.6c)
=– (2.6d)
2
3
2
1
2
2
2
2
3
−
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
cos
sin
cos
sin
π
θ
β
π
β
π
θ
β
π
β
π
θ
β
π
β
π
θ
β

153. Norton’s Fundamental Law of Cam Design:
The cam-follower function must have continuous
velocity and acceleration across the entire interval,
thus making the jerk finite.

154. Choosing Cam Functions
• They must obey the fundamental law
• Lower peak acceleration is better: F = ma
• Lower peak velocity lowers KE = 0.5 mv2
• Smoother jerk means lower vibrations
• Magnitude of jerk is poorly controlled in
manufacturing

155. Acceptable Double Dwell Function:
Cycloidal Motion

156. Acceptable Double
Dwell Function:
Modified Trapezoidal
Acceleration

157. Acceptable Double
Dwell Function:
Modified Sine
Acceleration

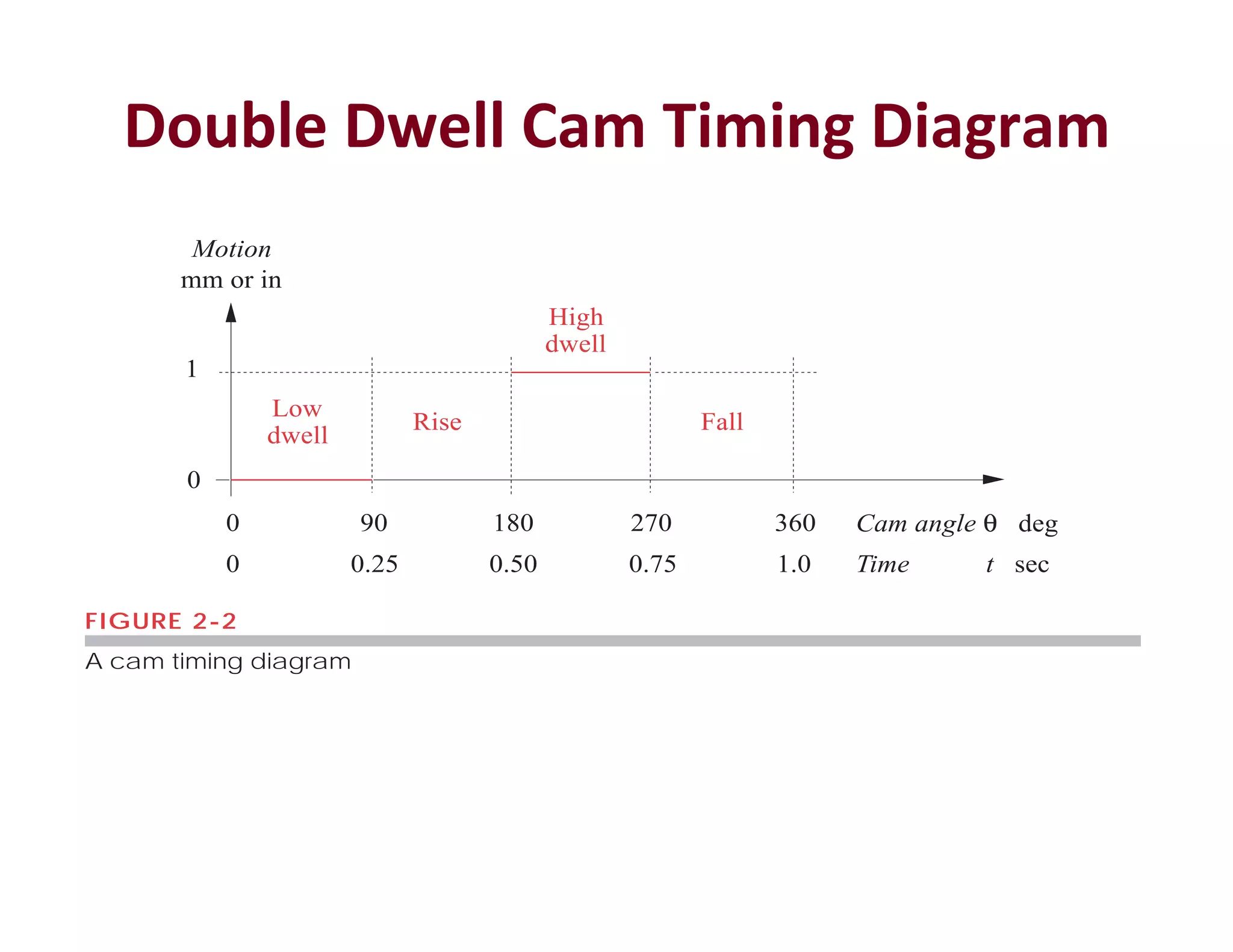
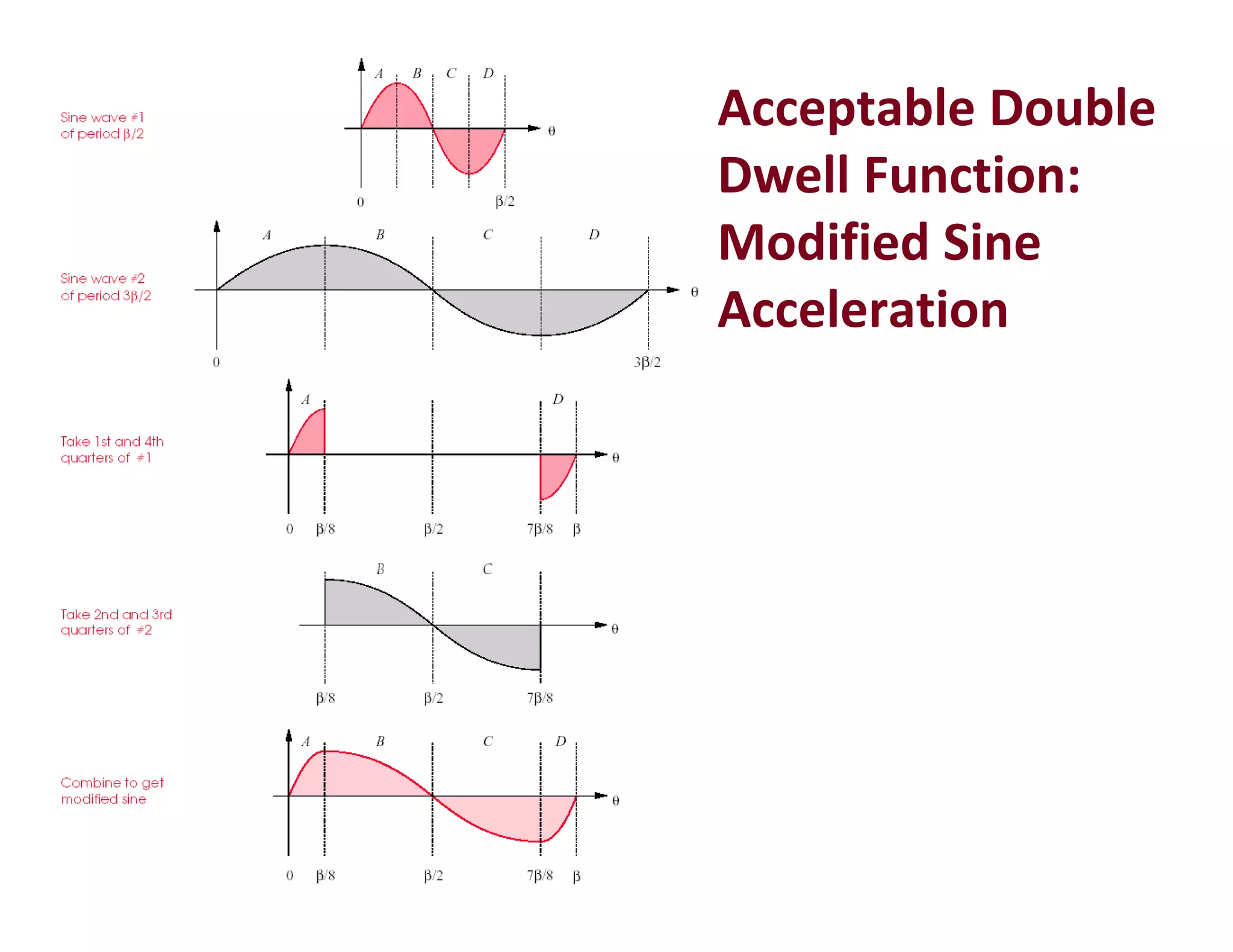
158. FIGURE 3-13
Minimum boundary conditions for the double-dwell case
(a)
(b)
(c)
(d )
h
0
s
v
0
a
0
j
0
Low
dwell
High
dwell
Rise Fall
deg
θ
deg
θ
deg
θ
deg
θ
β2
0 0
β1
β2
0 0
β1
β2
0 0
β1
β2
0 0
β1
Polynomial Functions
s C C x C x C x C x C x C x C x
n
n
= + + + + + + + +
0 1 2
2
3
3
4
4
5
5
6
6
3 19
 ( . )
when then
(a)
when then
θ
θ β
= = = =
= = = =
0 0 0 0
0 0
1
; , ,
; , ,
s v a
s h v a
v C C C C C
= +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
1
2 3 4 5
1 2 3
2
4
3
5
4
β
θ
β
θ
β
θ
β
θ
β
(d)
a C C C C
= +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
1
2 6 12 20
2 2 3 4
2
5
3
β
θ
β
θ
β
θ
β
(e)
s C C C C C C
= +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟ +
⎛
⎝
⎜
⎞
⎠
⎟
0 1 2
2
3
3
4
4
5
5
θ
β
θ
β
θ
β
θ
β
θ
β
(c)
0 0 0
0
0
0
= + + +
=
C
C

(f)
0
1
0 0
0
1
1
= + + +
[ ]
=
β
C
C

(g)
0
1
0 0
0
2 2
2
= + + +
[ ]
=
β
C
C

(h)
h C C C
= + +
3 4 5 (i)
0
1
3 4 5
3 4 5
= + +
[ ]
β
C C C (j)
0
1
6 12 20
2 3 4 5
= + +
[ ]
β
C C C ( )
k
C h C h C h
3 4 5
10 15 6
= = − =
; ; (l)

159. The 3‐4‐5 and 4‐5‐6‐7 Polynomials
3-4-5 Polynomial 4-5-6-7 Polynomial

160. Comparison of Five Double-Dwell Fcns

162. At the end of this video, you should be able to:
• Describe why a double‐dwell profile is not ideal for a single‐dwell
cam
• Construct the boundary conditions for a polynomial cam segment
• Solve for the coefficients of a polynomial cam segment
Cam Motion Design: Polynomial Deep Dive
Source: http://nptel.ac.in

163. Single Dwell Cam Design
• Rise: 1 inch in 90°
• Fall: 1 inch in 90°
• Dwell: 180°360°
2 Double‐Dwell Profiles?
Task: Rise‐Fall‐Dwell
Source: http://nptel.ac.in
0
ఉ
ଶ
ߚ
Cycloidal Rise Cycloidal Fall