Download to read offline
![29
OR = 3.9 [95% CI: 1.4-10.9]
CirculatoryDisease](https://image.slidesharecdn.com/kevincumminsstatpradoxes020316-160311193240/75/Kevin-Cummins-Statistical-Phenomenon-02-09-16-29-2048.jpg)
![30
CirculatoryDisease
OR = 1.3 [95% CI: 0.9-2.3]](https://image.slidesharecdn.com/kevincumminsstatpradoxes020316-160311193240/75/Kevin-Cummins-Statistical-Phenomenon-02-09-16-30-2048.jpg)
Uploaded byKevin Cummins
Kevin Cummins Statistical Phenomenon 02-09-16
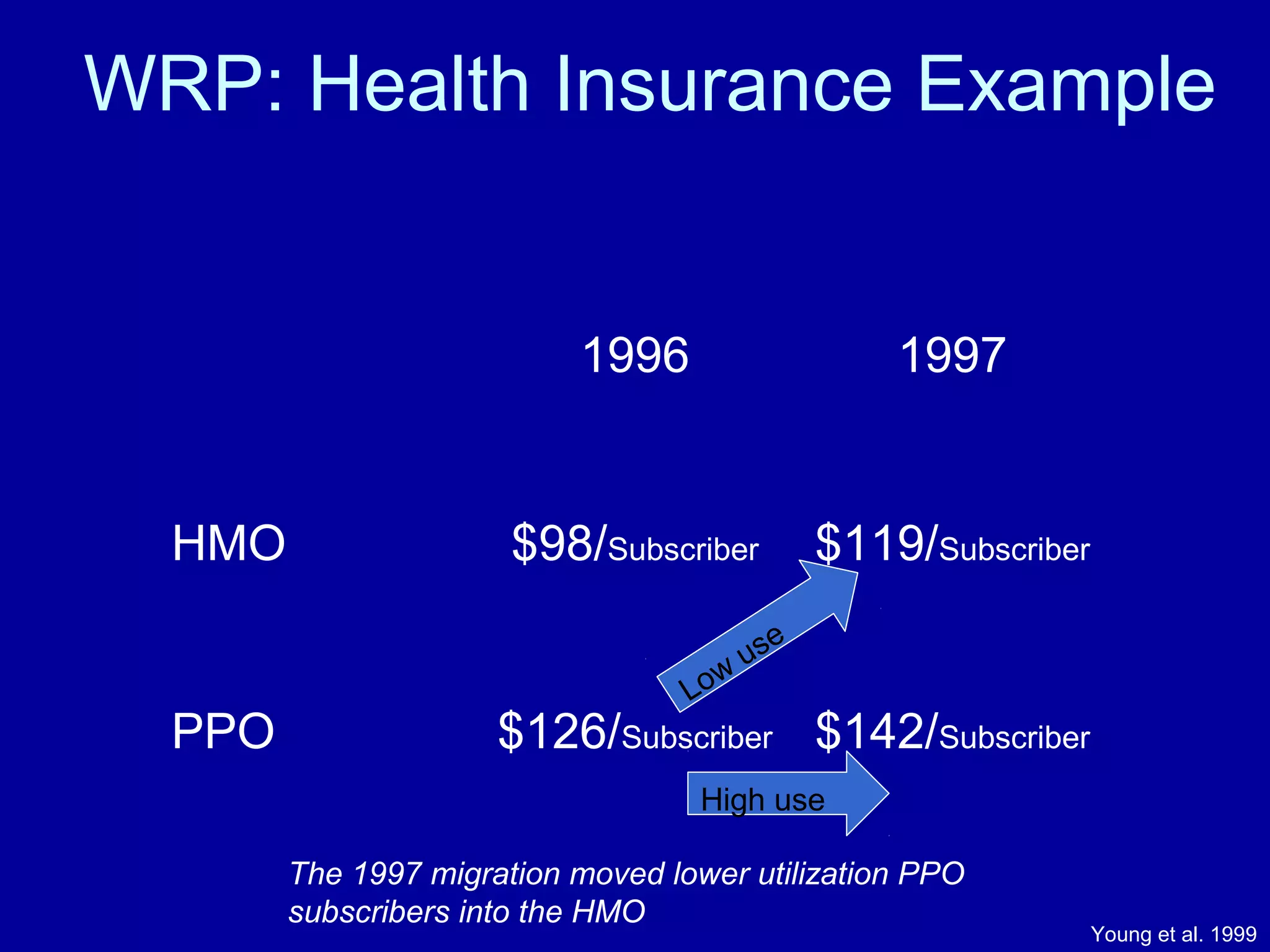
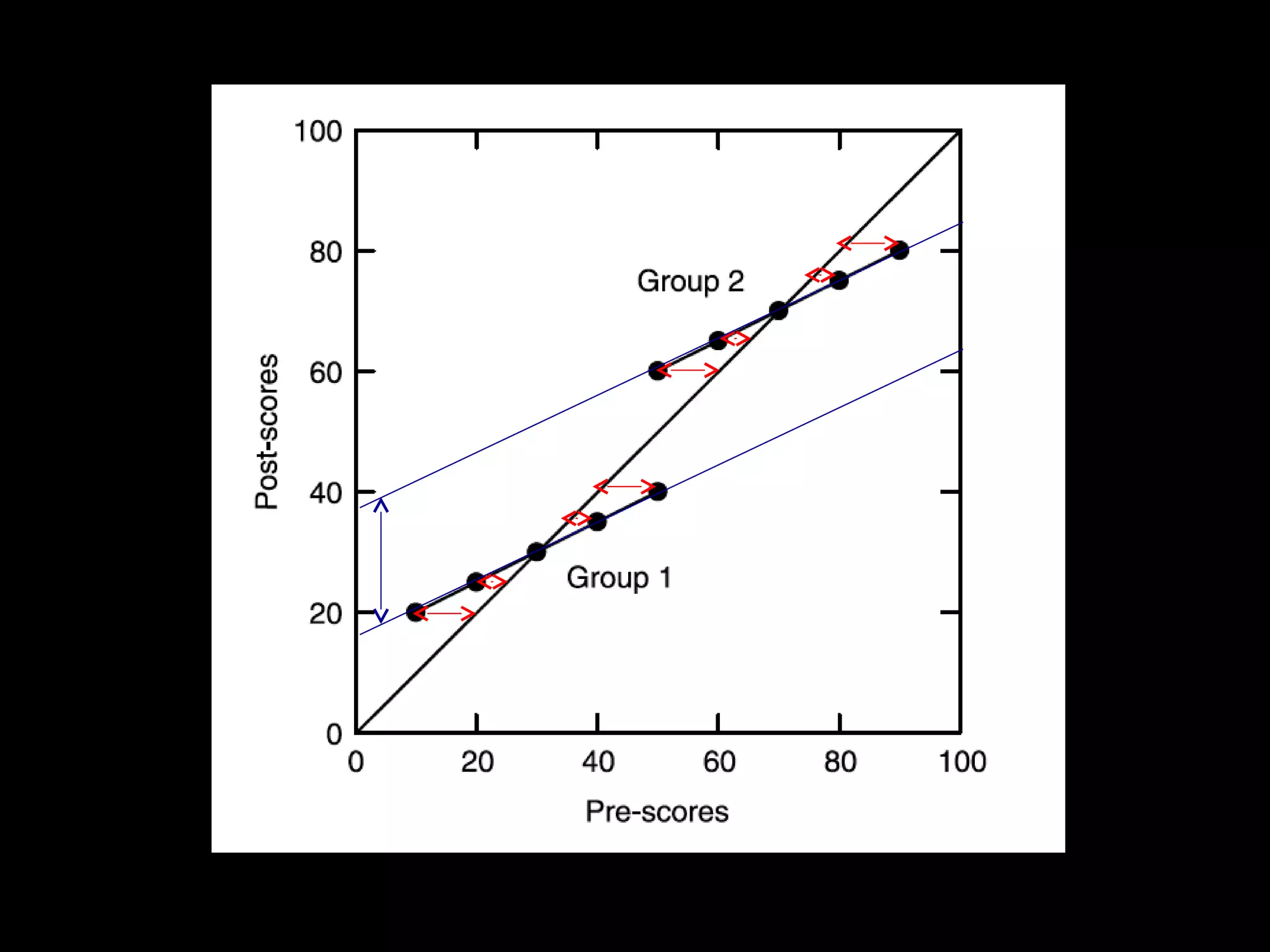
The document discusses several statistical paradoxes such as Simpson's Paradox, Will Rogers Paradox, Lord's Paradox, Berkson's Paradox, and the Monty Hall Problem, highlighting their implications in observational research. It provides definitions, outlines objectives for understanding these issues, and suggests remedies to mitigate their effects in statistical analysis. Additionally, it emphasizes the importance of proper study design and awareness of potential biases in interpreting data.
More Related Content
Similar to Kevin Cummins Statistical Phenomenon 02-09-16
Kevin Cummins Statistical Phenomenon 02-09-16
- 1. 1 Interesting Statistical Phenomenon San DiegoState University DSW/IRSU Brown Bag 3/16 Kevin Cummins
- 2. 2 Definitions • Principle: acomprehensive and fundamental law, doctrine, or assumption • Fallacy: a false or mistaken idea • Paradox: a statement that is seemingly contradictory or opposed to common sense and yet is perhaps true
- 3. 3 Outline • Objective • Simpson’sParadox • Will Roger’s Paradox • Lord’s Paradox • Berkson’s Paradox • Monte Hall Paradox • Others
- 4. 4 Objectives • Create awarenessof several statistical issues that might arise during observational research • Sneak in an introduction to mosaic plots • Learn how to win prizes on game shows
- 5. 5 Outline • Objective • Simpson’sParadox • Will Roger’s Paradox • Lord’s Paradox • Berkson’s Paradox • Monte Hall Paradox • Others
- 6. 6 Delayed On Time Alaska Airline 178 13% 1,338 88% America West 661 10% 5,804 90% WhichAirline Should You Fly? Cells contain counts and row %
- 7.
- 8. 8 Alaska Airlines AmericaWest .11 .05 .17 .14 .08 .29
- 9. 9 Simpson’s Paradox Occurs whenthe relationship between two (categorical) variables is reversed after a third variables is considered. The relationship between two variables differs within subgroups compared to that observed for the aggregated data.
- 10. 10 Simpson’s Paradox: Remedies/Responses Study Design UseExperiments Collect appropriate covariate data Know the Research System Collect appropriate covariate data Analytically introduce conditionals (i.e. moderators/covariates) Use appropriate interpretations
- 11. 11 Outline • Objective • Simpson’sFallacy • Will Roger’s Paradox • Lord’s Paradox • Berkson’s Paradox • Monte Hall Paradox • Others
- 12. WRP: Health InsuranceExample 1996 1997 HMO $98/Subscriber $119/Subscriber PPO $126/Subscriber $142/Subscriber PPO No Longer Free Young et al. 1999 Cells are cost to employer (a hospital system) Expected Lower Expenditures
- 13. 13 Will Roger’s Paradox “Whenthe Okies left Oklahoma and moved to California, they raised the average intelligence level in both states.” IC: uspsstamps.com
- 14. 14 The Will RogersParadox (WRP) is observed when moving an element from one set to another set the mean values of both sets change in the same direction. The effect will occur when both of these conditions are met: 1. The element being moved is below average for its current set. 2. The element being moved is above the current average of the set it is entering.
- 15. 15 WRP: Effect ofShifting One Observation
- 16. WRP: Health InsuranceExample 1996 1997 HMO $98/Subscriber $119/Subscriber PPO $126/Subscriber $142/Subscriber The 1997 migration moved lower utilization PPO subscribers into the HMO Young et al. 1999 Low use High use
- 17. 17 Will Rogers: Remedies/Responses Know YourSystem In This Case: Statistically adjust/stratify for baseline costs
- 18. 18 Outline • Objective • Simpson’sFallacy • Will Roger’s Paradox • Lord’s Paradox • Berkson’s Paradox • Monte Hall Paradox • Others
- 19. 19 Lord’s Paradox • Occursin situations where change score analysis and ANCOVA yield apparently conflicting results
- 20. 20 An Extreme Example •Assessment of a supplemental educational program • 10 schools, 5 schools opted into the programs (free-choice) • 1 student from each school assessed • Pre and post assessments given • No random/sampling/measurement error (simplified)
- 22. 22 Two Statisticians Statistician One •Calculates difference scores for each group • Change scores are the same for both groups Statistician Two • Adjusts for initial score • Finds group differences
- 23. 23 Two Statisticians Paired t-Test StatisticianOne Data: group 1 vs. group 2 t = -0.002, df = 299, p-value = 0.99 ANCOVA Statistician Two Coefficients: Value Pr(>|t|) (Intercept) 15.0 0.00 Pre 0.5 0.00 Group 20.0 0.00 y1 = 0 y2 = 0
- 25. 25 Lord’s Paradox: Remedies/Responses “With thedata available…there is no logical or statistical procedure that can be counted on to make allowances for pre-existing conditions between groups.” Frederic Lord •Know your system – Match your samples •Use the best descriptive statement(s) that match your questions •Use and report multiple approaches (Wright 2006) •Graph your data
- 26. 26 Outline • Objective • Simpson’sFallacy • Will Roger’s Paradox • Lord’s Principle • Berkson’s Paradox • Monte Hall Paradox • Others
- 27. 27 Berkson’s Paradox An associationreported from a hospital case-control study can be distorted If cases and controls experience differential hospital admission rates with respect to the suspected causal factor
- 28. 28 Typical Berkson Scenario Examplefrom Roberts et al. 1978 Investigated the relationship between circulatory and respiratory disease. Sampled the general population and hospital populations.
- 29. 29 OR = 3.9[95% CI: 1.4-10.9] CirculatoryDisease
- 30. 30 CirculatoryDisease OR = 1.3[95% CI: 0.9-2.3]
- 31. 31 Berkson Example Example fromLilienfeld and Stolley (1994) • No greater admission rate for subjects with multiple conditions • Different rates of admission for cases and controls • Results in an apparent association between two conditions
- 32. Disease B Disease ACase Control Case 200 200 Control 800 800 Total 1000 1000 % with A 20 20 Disease B Disease A Case Control Case Control Total % with A 110 170 80 560 Community Hospital P(H|A)=.50 P(H|B)=.10 P(H|!B)=70 100 X .50 X .10 X .50 X .70 100 X .70X .10 190 730 58 23 OR=1 OR=4.5
- 33. 33 Berkson’s: Remedies/Responses –There is nosafe analytical mitigation –Analysis of potential bias • know your system • Sensitivity analysis –Limit conclusions –Utilize multiple control pools –Consider alternative study design
- 34.
- 35.
- 36. 36 Miller et al.1989
- 37. 37 Review Big Picture Use careto interpret observational studies Know your system Conditional Responses Simpson’s Lord’s Will Roger’s Perspective Problems Berkson’s Monte Hall
- 38. Doctor Tyrano, Lookfor a Covariate! Cartoon used with with permission
- 39. 39 Benford’s Law Ones arethe most common leading digit in most data. Notice that if a data entry (base 10) begins with a 1, the entry has to be at least doubled to have a first significant digit of 2. However, if a leading digit begins with a 9, it only has to be increased by, at most, 11% to change the first significant digit into a 1.
- 40. 40 Lindley’s Paradox • StandardSampling Theory VS. Bayesian Theory Under some circumstances strong evidence against the null hypothesis doesn’t result in the null being rejected