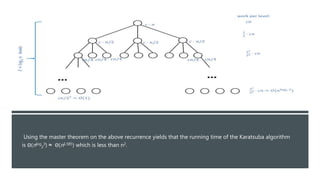
The Karatsuba algorithm reduces the time complexity of multiplying two n-digit numbers from the conventional O(n^2) to O(n^1.585). It does this by dividing the numbers into halves at each recursive step and performing only three multiplications of the halves rather than the four required by the basic multiplication algorithm. This reduction in the number of multiplications means the overall time complexity improves to O(n^1.584...) which is superior to O(n^2).

1. KARATSUBA
ALGORITHM
FOR FAST
MLTIPLICATION

2. CONVENTIONAL METHOD OF MULTIPLICATION AND ITS
COMPLEXITY
 The Naive approach for multiplication is the process that we study in school.
 Conventional method of n digit multiplication total n*n=n2 multiplication is required.
let’s take an example of 2-digit multiplication…
6 5 * 9 7 == 6 3 0 5
 Here first 7 is multiplied by 5 and then 6. It makes two multiplication.
 Again 9 is multiplied by 5 and then 6. It also make two multiplication.
So, total multiplication required is 4.
As we can say n*n=n2 multiplication is required.

3. KARATSUBA MULTIPLICATION
 This algorithm reduces the number of multiplication comparing to conventional method of
multiplication.
 Using Divide and Conquer, we can multiply two integers in less time complexity. We divide
the given numbers in two halves. Let the given numbers be X and Y.
Let, X = 1 2 3 4
Y = 9 8 7 6 Here n = 4
Here we divide the number into two halves
a = 1 2 b = 3 4
c = 9 8 d = 7 6

4. Here we can write X and Y as..
X = a*10n/2 + b Y = c*10n/2 + d
Let’s multiply X and Y
X * Y = (a*10n/2 + b ) (c*10n/2 + d)
= (10n)ac + (10n/2)(ad + bc) + bd
Here in each step of recursive call we are performing 4 extra multiplication and two extra atomic
addition.
In each step two chopped number is passed to recursive function whose length reduces to ½
times each steps.
Overall function becomes
M(n) = 4M(n/2) + O(n) (two atomic addition performs in each steps).

5. The tricky part of this algorithm is to change the middle two terms to some other form so that
only one extra multiplication would be sufficient.
Here we can write
ad + bc = (a + b) (c + d) – ac – bd
We are reducing one extra multiplication and now our function becomes….
M(n) = 3M(n/2) + O(n)
By doing this we are performing 3 extra multiplications of size n/2 in each step.

6. Using the master theorem on the above recurrence yields that the running time of the Karatsuba algorithm
is Θ(nlog
2
3) ≈ Θ(n1.585) which is less than n2.

7. COMPLEXITY OF KARATSUBA ALGORITHM
Notice that each time digit is reduced by ½ times the previous ones , thus we can write…
n = 2k
log2n = k log22
k = log2n
For conventional multiplication 4k = 4log
2
n = 2(log 4)(log n) =n(log 4) = n2
For karatsuba multiplication 3k = 3log
2
n = 2(log 3)(log n) = n(log 3) = n1.584…
As we can see that complexity of multiplication reduced to n1.584…