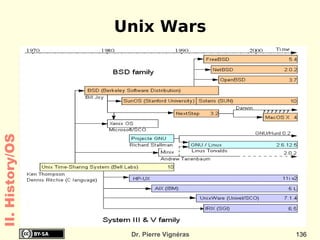
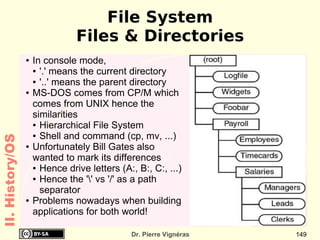
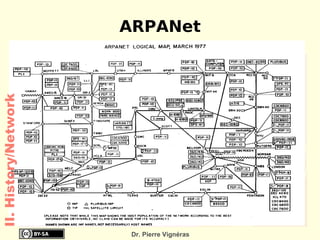
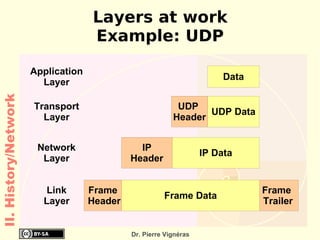
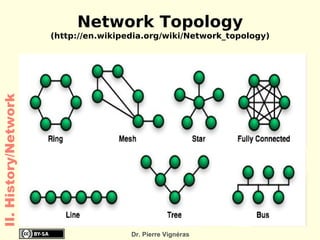
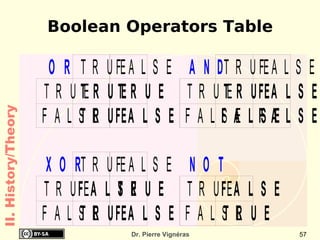
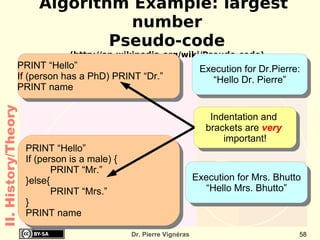
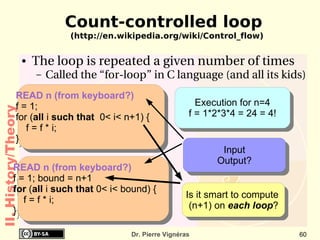
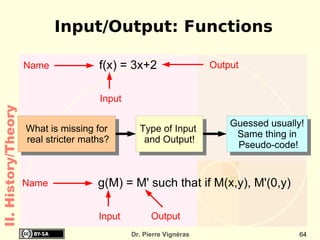
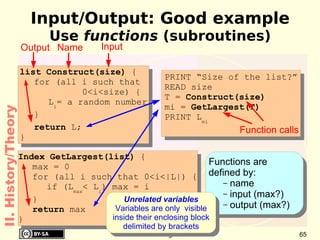
This document provides an overview of the history of computing including:
- Early counting methods like the abacus and mechanical counting devices.
- The development of punched card systems in the late 19th century.
- The creation of the Z3 computer in 1941 which used binary representation.
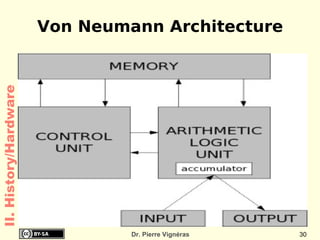
- The development of the Von Neumann architecture in the 1940s which is still used today.
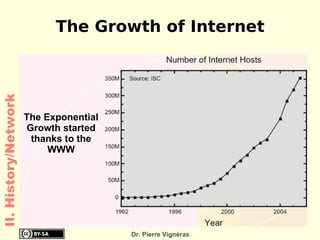
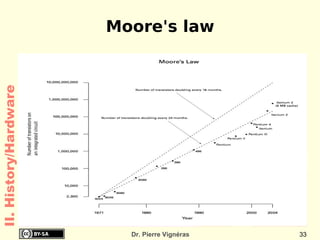
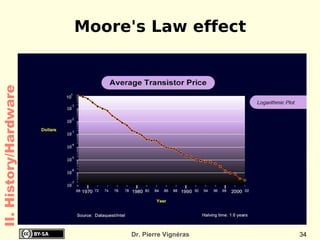
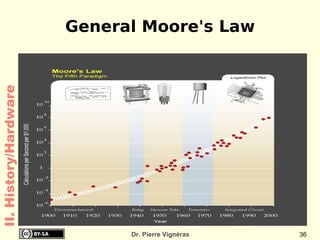
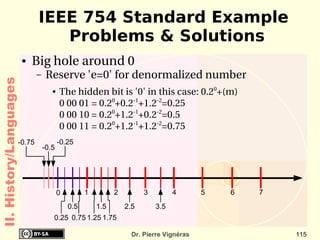
- Moore's Law from 1965 which predicted computing power would double every 18 months.


















































![AMD: Athlon 64, Opteron (~ 2 Ghz) Memory: [512 – 1512] MB](https://image.slidesharecdn.com/itc-090728124221-phpapp01/85/History-of-Computing-66-320.jpg)
![Hard Drives: [60 – 800 ] GB](https://image.slidesharecdn.com/itc-090728124221-phpapp01/85/History-of-Computing-67-320.jpg)






![You need a client application (called a web browser) URL: protocol://address[:port]/ressource http://images.google.com/preferences (www)](https://image.slidesharecdn.com/itc-090728124221-phpapp01/85/History-of-Computing-75-320.jpg)


![Yahoo: http://www.yahoo.com How does it work? During the night, a robot scans the web and indexes web pages making pairs [word, {URLs}]](https://image.slidesharecdn.com/itc-090728124221-phpapp01/85/History-of-Computing-78-320.jpg)
![When you enter a keyword, the search engine look in its table for a matching [word, {URLs}]](https://image.slidesharecdn.com/itc-090728124221-phpapp01/85/History-of-Computing-79-320.jpg)





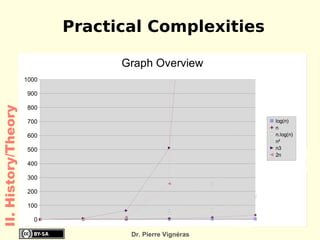
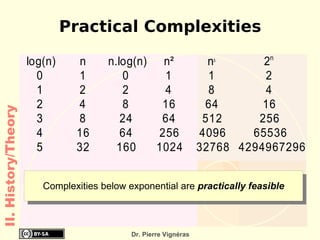

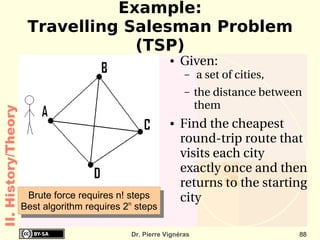










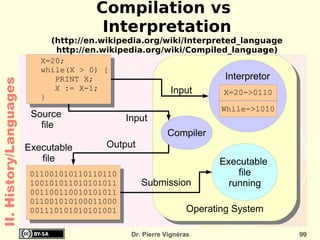










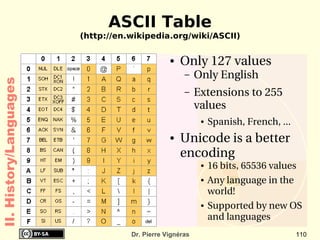



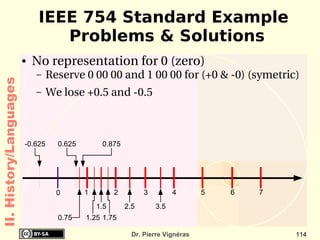



![Quoted as “[...] doubles every 18 months ”! Empirical Observations and prediction goal for an entire industry. Moore's law means an average performance improvement in the industry as a whole of over 1% a week. A new product that is expected to take three years to develop and is just two or three months late is 10 to 15% slower, bulkier, or lower in storage capacity! II. History/Hardware](https://image.slidesharecdn.com/itc-090728124221-phpapp01/85/History-of-Computing-119-320.jpg)