This document provides an introduction to time series analysis, including definitions of autoregressive (AR), moving average (MA), and autoregressive moving average (ARMA) models. It discusses the stationary data assumption and how differencing can be used to transform non-stationary data into stationary data. Specifically, it shows an example of applying 1-lag and 2-lag differencing to a time series data set.

1. Introduction to Time Series Analysis
AR, MA, ARMA, Stationary Data, & Differencing

2. Time Series Data
• Definition
Data that change over time, e.g., stock price, sales growth.
• Stock Price Analysis Example

3. AR, MA, and ARMA Model
• Autoregressive (AR) Model
• Moving Average (MA) Model
• Autoregressive Moving Average (ARMA) Model
𝑦𝑡 = β0 + β1𝑦𝑡−1 + β2𝑦𝑡−2 + β3𝑦𝑡−3 + ⋯ + β𝑝𝑦𝑡−𝑝
𝑦𝑡 = ε𝑡 + ɵ1ε𝑡−1 + ɵ2ε𝑡−2 + ⋯ + ɵ𝑞ε𝑡−𝑞
𝑦𝑡 = β1𝑦𝑡−1 + β2𝑦𝑡−2 + β3𝑦𝑡−3 + ⋯ + β𝑝𝑦𝑡−𝑝 +
ε𝑡 + ɵ1ε𝑡−1 + ɵ2ε𝑡−2 + ⋯ + ɵ𝑞ε𝑡−𝑞

4. Stationary Data Assumption
• The mean and variance of a time series are constant for
the whole series, no matter where you choose a period.

5. Differencing
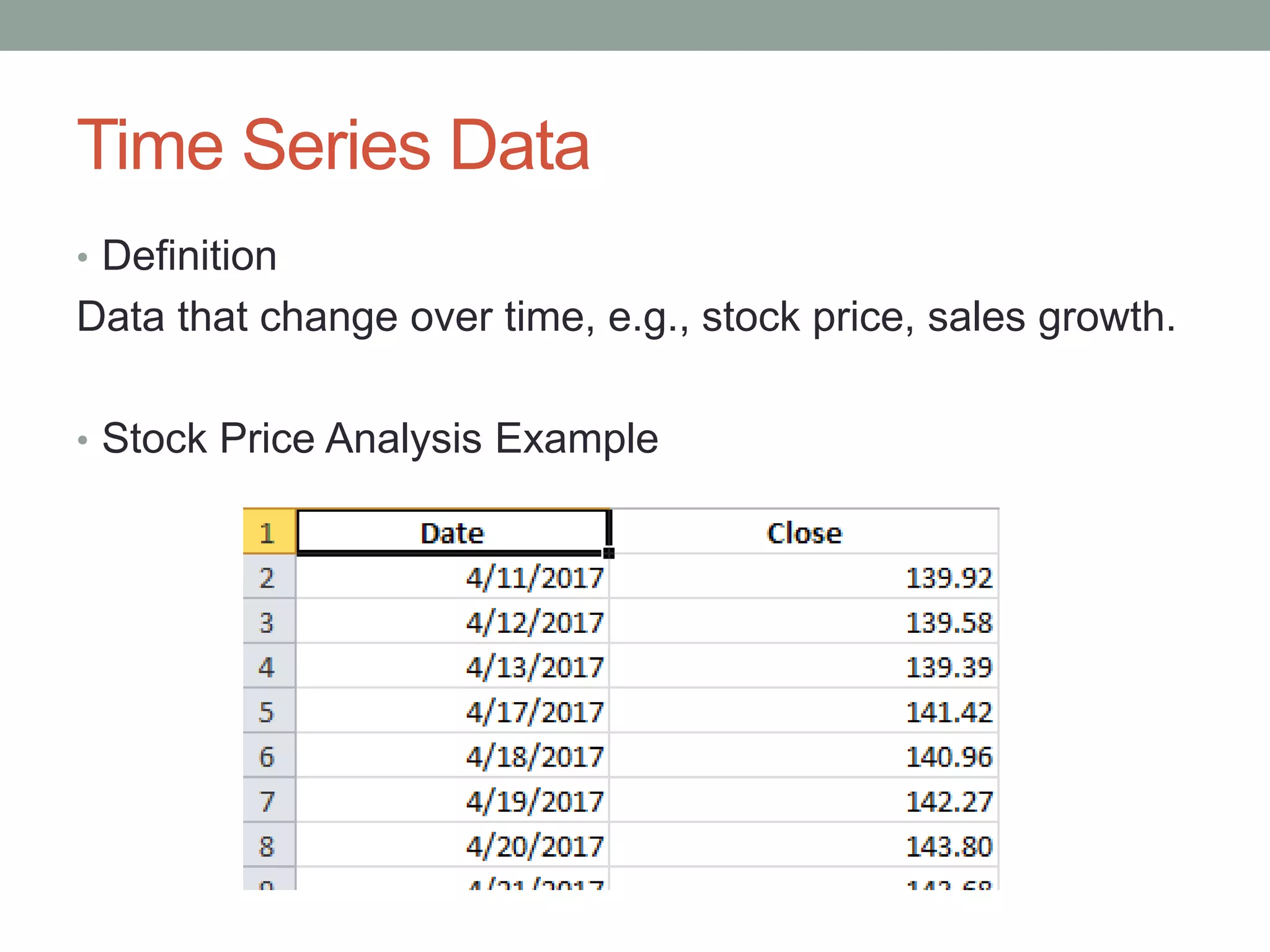
• The process of subtracting one observation from another.
• Used for transforming non-stationary data into stationary
data.
• Example
X=[5, 4, 6, 7, 9, 12]
What should be the values of X after 1-lag differencing?
X* =[1, -2, -1, -2, -3]

6. 1-Lag Differencing Twice vs. 2-Lag
Differencing Once
X=[5, 4, 6, 7, 9, 12]
What should be the values of X after 1-lag twice?
1-lag differencing once:
X*=[1, -2, -1, -2, -3]
1-lag differencing again (i.e., 1-lag differencing twice):
X**=[3, -1, 1, 1]

7. 1-Lag Differencing Twice vs. 2-Lag
Differencing Once
X=[5, 4, 6, 7, 9, 12]
What should be the values of X after 2-lag once?
2-lag differencing once:
X’=[-1, -3, -3, -5]
We can also do 4-lag differencing once, 12-lag differencing
once, etc. Can you see where to use them?
Answer: Processing seasonal data!