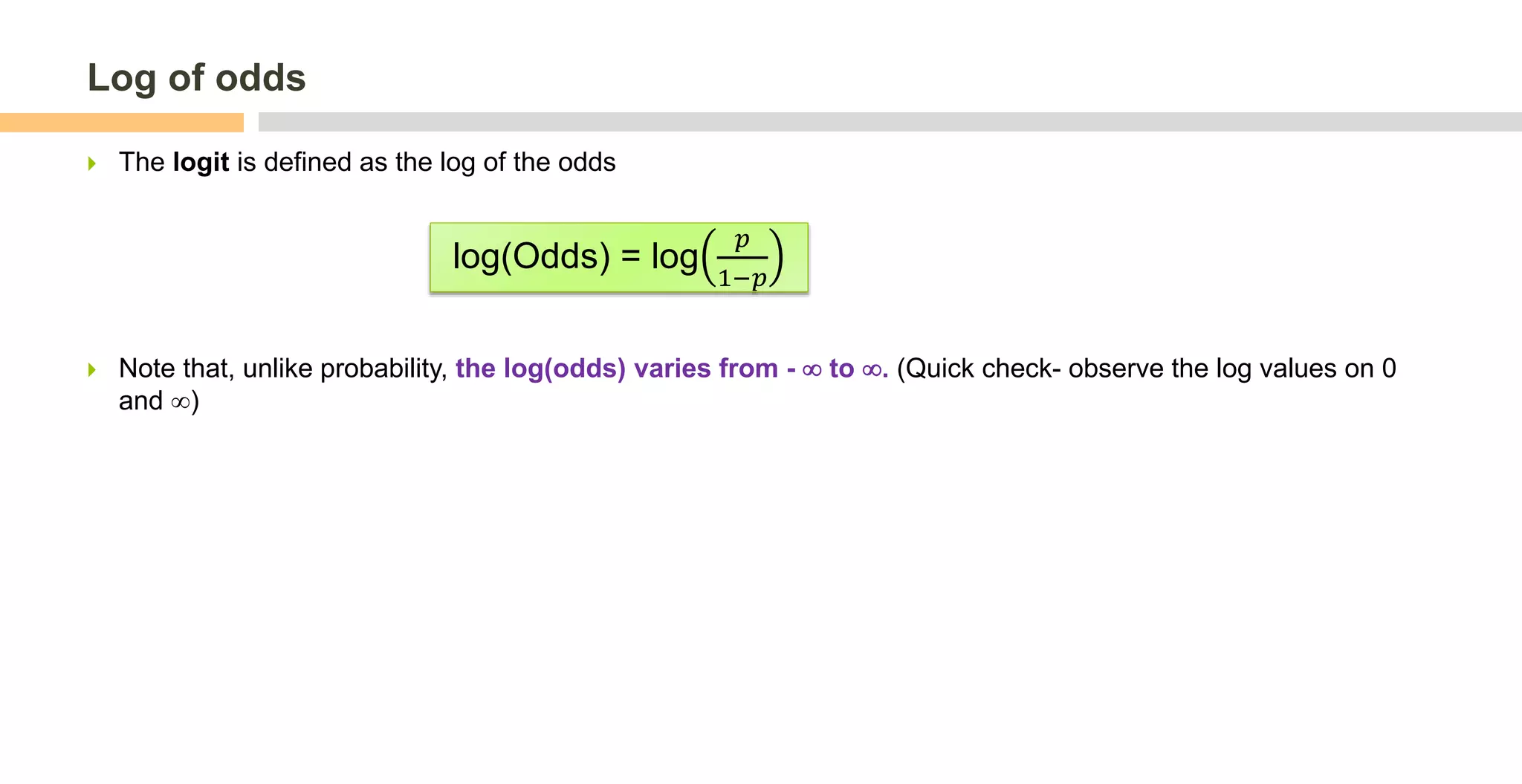
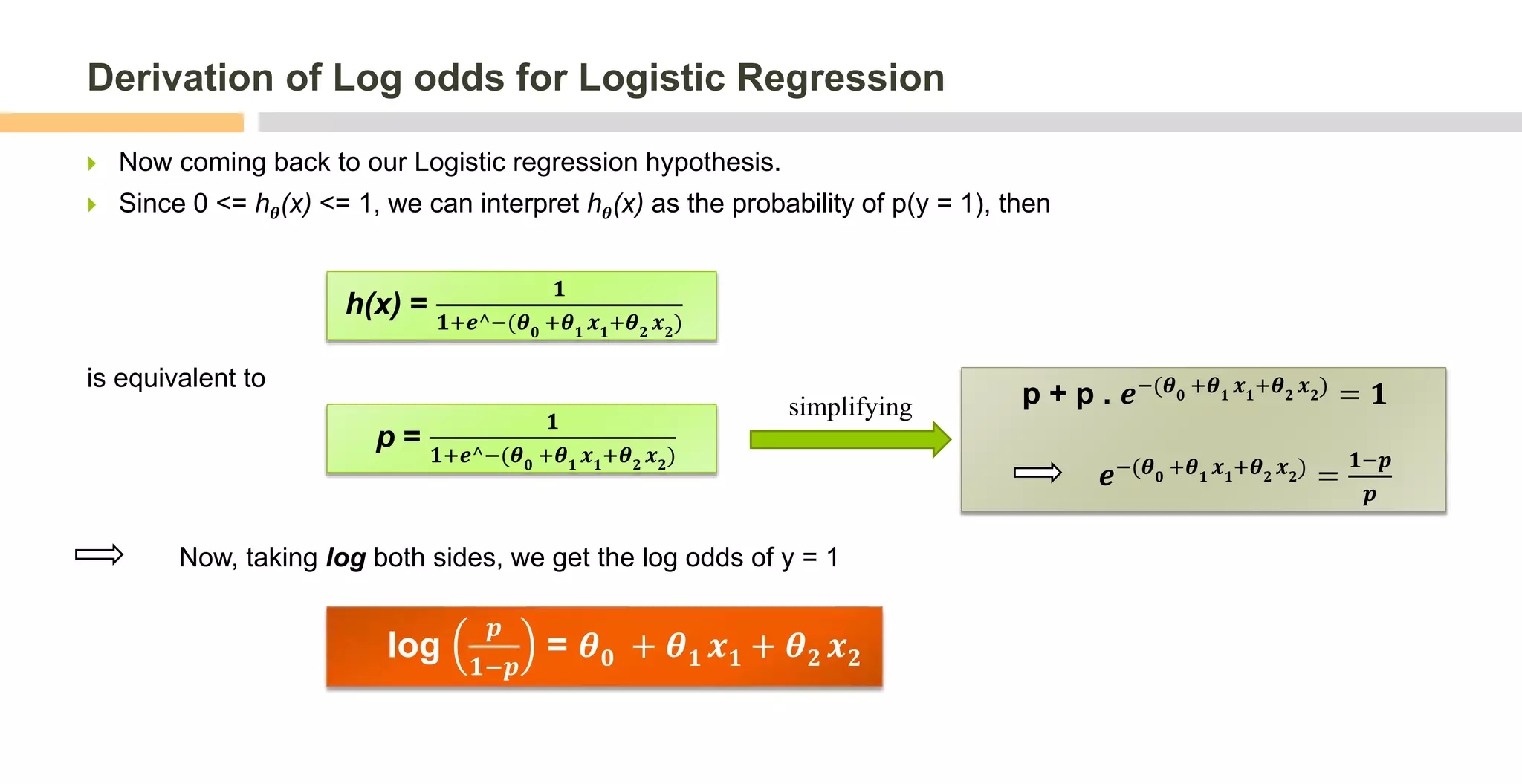
This document discusses the interpretation of coefficients in linear and logistic regression models. For linear regression, the coefficients directly represent the relationship between the predictor and response variables. For logistic regression, the coefficients represent the effect of the predictors on the log odds of the response being 1. Taking the exponent of the linear combination of coefficients and predictors gives the odds, which can be converted to a probability between 0 and 1 using the sigmoid function.

1. Interpretation of coefficients in
Linear and Logistic Regression
Prepared by
Ankit Sharma
Email: 27ankitsharma@gmail.com

2. Linear regression
 In Linear Regression, it is very easy to interpret the coefficients due to the simple form of hypothesis. For two
predictor variable x1 and x2 and a dependent variable y, we have
 Interpretation of θ1 :
 If you increase x1 by 1 unit but do not touch x2 at all, y will increase by θ1 unit (or decrease if θ1 is negative).
 Same goes for interpretation of θ2.
 θ0 is the value of y when x1 and x2 both are 0.
 Example: Suppose we have θ0 = 5, θ1 = 0.41, θ2 = -1.3
 When x1 increases by 1 unit, y increases by 0.41 unit provided x2 remains constant.
 When x2 increases by 1 unit, y decreases by 1.3 unit provided x1 remains constant
 y = 5 when x1 = x2 = 0
y = θ0 + θ1 x1 + θ2 x2

3. Logistic regression
 In Logistic regression, we pass our Linear regression hypothesis (θ0 + θ1 x1 + θ2 x2) into sigmoid function to
squash it in [0, 1]
Now we have 0 ⩽ hθ(x) ⩽1
 Prediction
 We set a "threshold" at 0.5 (better threshold can also be derived from ROC curve) and
o if hθ(x) ⩾ 0.5  we predict y =1
o if hθ(x) < 0.5  we predict y = 0
hθ (x) =
𝟏
𝟏+𝒆^−(𝜽 𝟎
+𝜽 𝟏
𝒙 𝟏
+𝜽 𝟐
𝒙 𝟐
)
Image source: saedsayad.com
Due to complex process of getting y from x’s, we can not easily interpret the
effect of change in x’s on y ! Therefore we try to simplify this expression.

4. Odds
 Before we dive into the interpretation of Logistic Regression coefficients, let’s understand the odds first:
 If the probability of an event is p then the odds of that event are calculated as:
 For example, If there is a 0.8 probability of raining tomorrow, then we can say that out of 10 times, it is 8 times likely to
rain.
 Now let’s calculate the odds of raining from its probability:
 In terms of Odds, we can say that every 2 times when it rains, 1 time it does not. That is, the odds of
raining tomorrow are 2:1.
 Note that, unlike probability, the odds varies from 0 to  .
Odds =
0.8
1−0.8
=
0.4
0.2
=
2
1
Odds =
𝑝
1−𝑝

5. Log of odds
 The logit is defined as the log of the odds
 Note that, unlike probability, the log(odds) varies from -  to . (Quick check- observe the log values on 0
and )
log(Odds) = log
𝑝
1−𝑝

6. Derivation of Log odds for Logistic Regression
 Now coming back to our Logistic regression hypothesis.
 Since 0 <= h 𝜽(x) <= 1, we can interpret h 𝜽(x) as the probability of p(y = 1), then
is equivalent to
Now, taking log both sides, we get the log odds of y = 1
log
𝒑
𝟏−𝒑
= 𝜽 𝟎 + 𝜽 𝟏 𝒙 𝟏 + 𝜽 𝟐 𝒙 𝟐
p + p . 𝒆−(𝜽 𝟎
+𝜽 𝟏
𝒙 𝟏
+𝜽 𝟐
𝒙 𝟐
) = 𝟏
𝒆−(𝜽 𝟎
+𝜽 𝟏
𝒙 𝟏
+𝜽 𝟐
𝒙 𝟐
) =
𝟏−𝒑
𝒑
h(x) =
𝟏
𝟏+𝒆^−(𝜽 𝟎
+𝜽 𝟏
𝒙 𝟏
+𝜽 𝟐
𝒙 𝟐
)
p =
𝟏
𝟏+𝒆^−(𝜽 𝟎
+𝜽 𝟏
𝒙 𝟏
+𝜽 𝟐
𝒙 𝟐
)
simplifying

7. Interpretation of coefficients..
 Copying last expression from previous slide:
Interpretation of coefficients: (Remember, p = P(y = 1))
 One unit increase in x1, will increase log(odds) of (y = 1) by θ1 unit provided x2 is kept constant. Similarly for θ2.
 Interpretation of θ0 remains same as in Linear regression.
We can also see that:
• In Linear regression, y is assumed to be a linear function of x’s,
• In Logistic regression, log odds of y assumed to be a linear function of x’s.
log
𝒑
𝟏−𝒑
= 𝜽 𝟎 + 𝜽 𝟏 𝒙 𝟏 + 𝜽 𝟐 𝒙 𝟐

8. Thank You