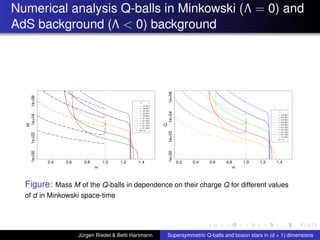
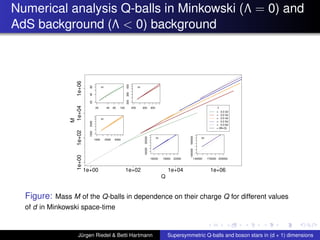
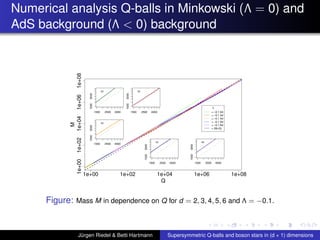
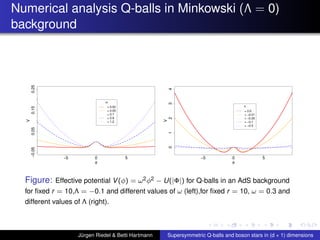
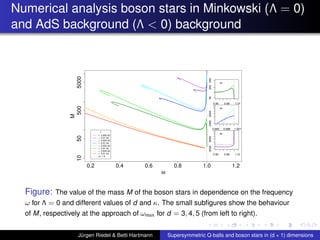
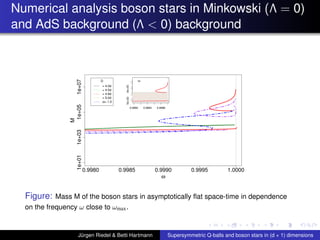
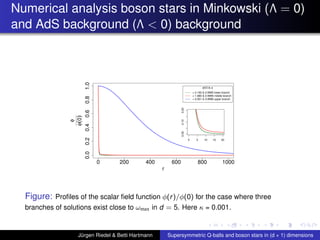
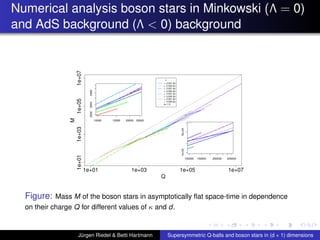
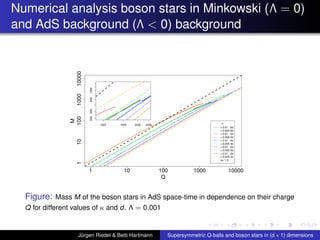
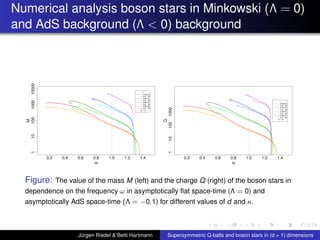
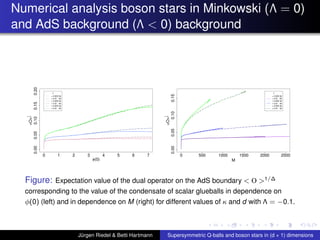
This document summarizes a talk on supersymmetric Q-balls and boson stars in (d+1) dimensions. It introduces Q-balls and boson stars as non-topological solitons stabilized by a conserved Noether charge. It discusses properties like existence conditions and the thin wall approximation for Q-balls. For boson stars, it covers different models and properties like rotating and charged boson stars. The document also discusses applications like the AdS/CFT correspondence and holographic superconductors using boson stars in anti-de Sitter spacetime.







![The model
Lagrangian L =∂µΦ∂µΦ∗ − U(|Φ|); the signature of the
metric is (+,-,-,-)
Noether current j = i(Φ∗ ˙Φ − Φ ˙Φ∗) symmetry under U(1)
Conserved Noether charge Q = 1
i d3(Φ∗ ˙Φ − Φ ˙Φ∗), with
Φ := Φ(t, r) we have dQ
dt = 0
Ansatz for solution Φ(x, t) = φ(x)eiωt
Energy-momentum tensor
Tµν = ∂µΦ∂νΦ∗ + ∂νΦ∂µΦ∗ − gµνL
Total Energy E = d3xT0
0 = d3x[| ˙Φ|2 + | Φ|2 + U(|Φ|)]
under assumption that gµν is time-independent
Jürgen Riedel & Betti Hartmann Supersymmetric Q-balls and boson stars in (d + 1) dimensions](https://image.slidesharecdn.com/internalworkshopjubtalkjan2013-140608032140-phpapp02/85/Internal-workshop-jub-talk-jan-2013-8-320.jpg)
![Existence conditions of Q-balls
Condition 1
V (0) < 0; Φ ≡ 0 local maximum ⇒ ω2 < ω2
max ≡ U (0)
Condition 2
ω2 > ω2
min ≡ minφ[2U(φ)/φ2] minimum over all φ
Consequences
Restricted interval ω2
min < ω2 < ω2
max ;
U (0) > minφ[2U(φ)/φ2]
Q-balls are rotating in inner space with ω stabilized by
having a lower energy to charge ratio as the free particles
Jürgen Riedel & Betti Hartmann Supersymmetric Q-balls and boson stars in (d + 1) dimensions](https://image.slidesharecdn.com/internalworkshopjubtalkjan2013-140608032140-phpapp02/85/Internal-workshop-jub-talk-jan-2013-9-320.jpg)















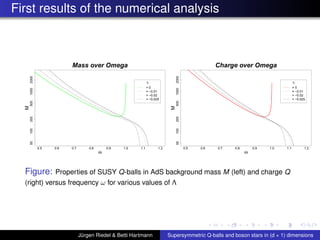
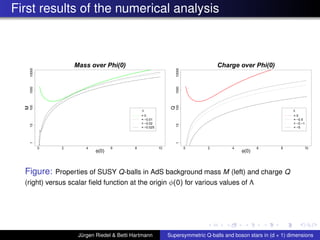
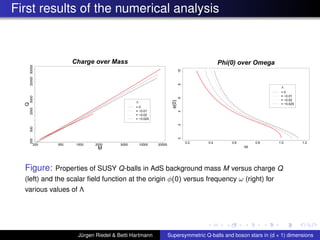
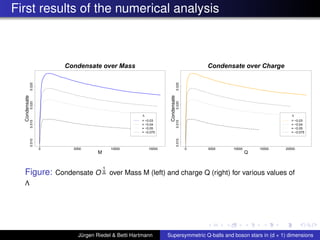
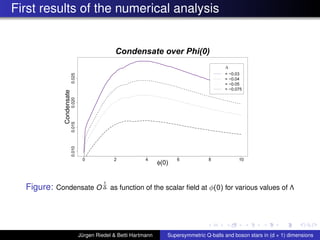


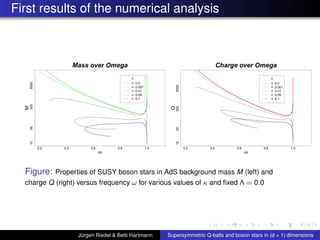
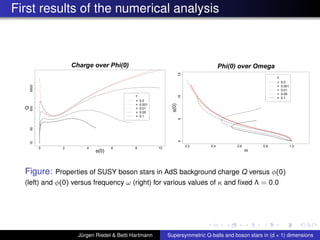
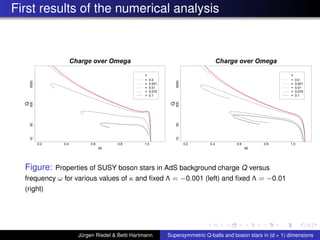
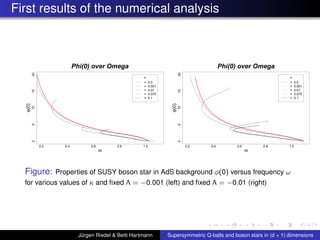
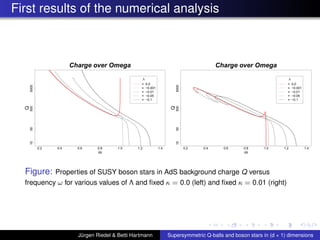
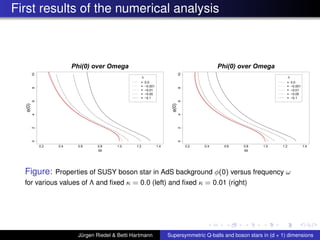

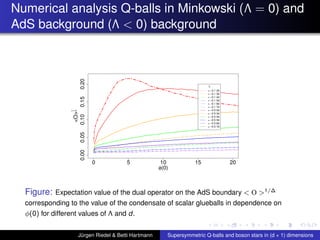
![Summary of first Results continued
For boson stars the cosmological constant Λ ’kills’ the
local maximum of the charge Q and Mass M near ωmax ,
similarly as large values of κ
The curve of the condensate for Q-balls, i.e. O
1
∆ as a
function of the scalar field φ(0), has qualitatively the
same shape as in Horowitz and Way, JHEP 1011:011, 2010
[arXiv:1007.3714v2]
Jürgen Riedel & Betti Hartmann Supersymmetric Q-balls and boson stars in (d + 1) dimensions](https://image.slidesharecdn.com/internalworkshopjubtalkjan2013-140608032140-phpapp02/85/Internal-workshop-jub-talk-jan-2013-39-320.jpg)