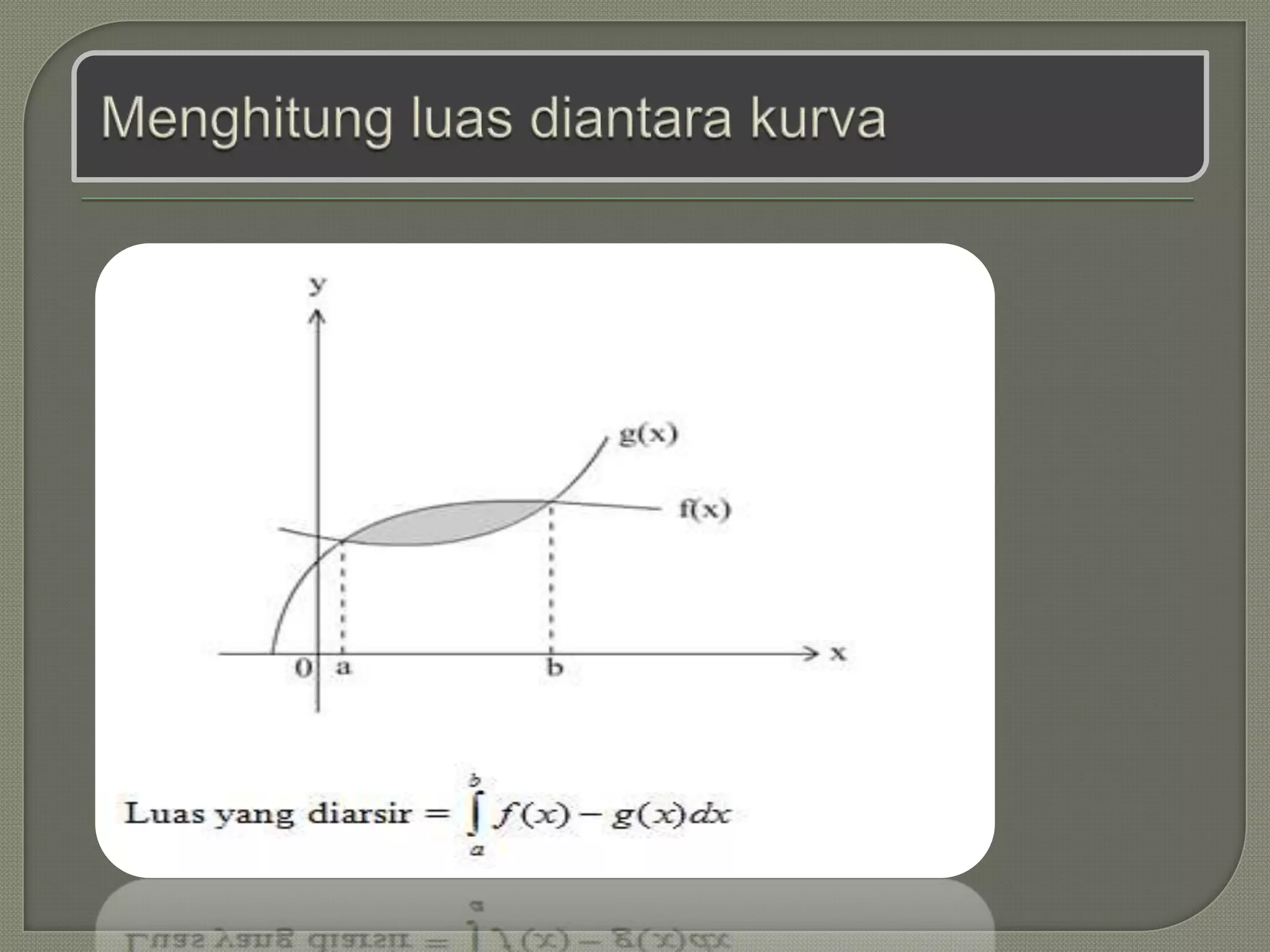
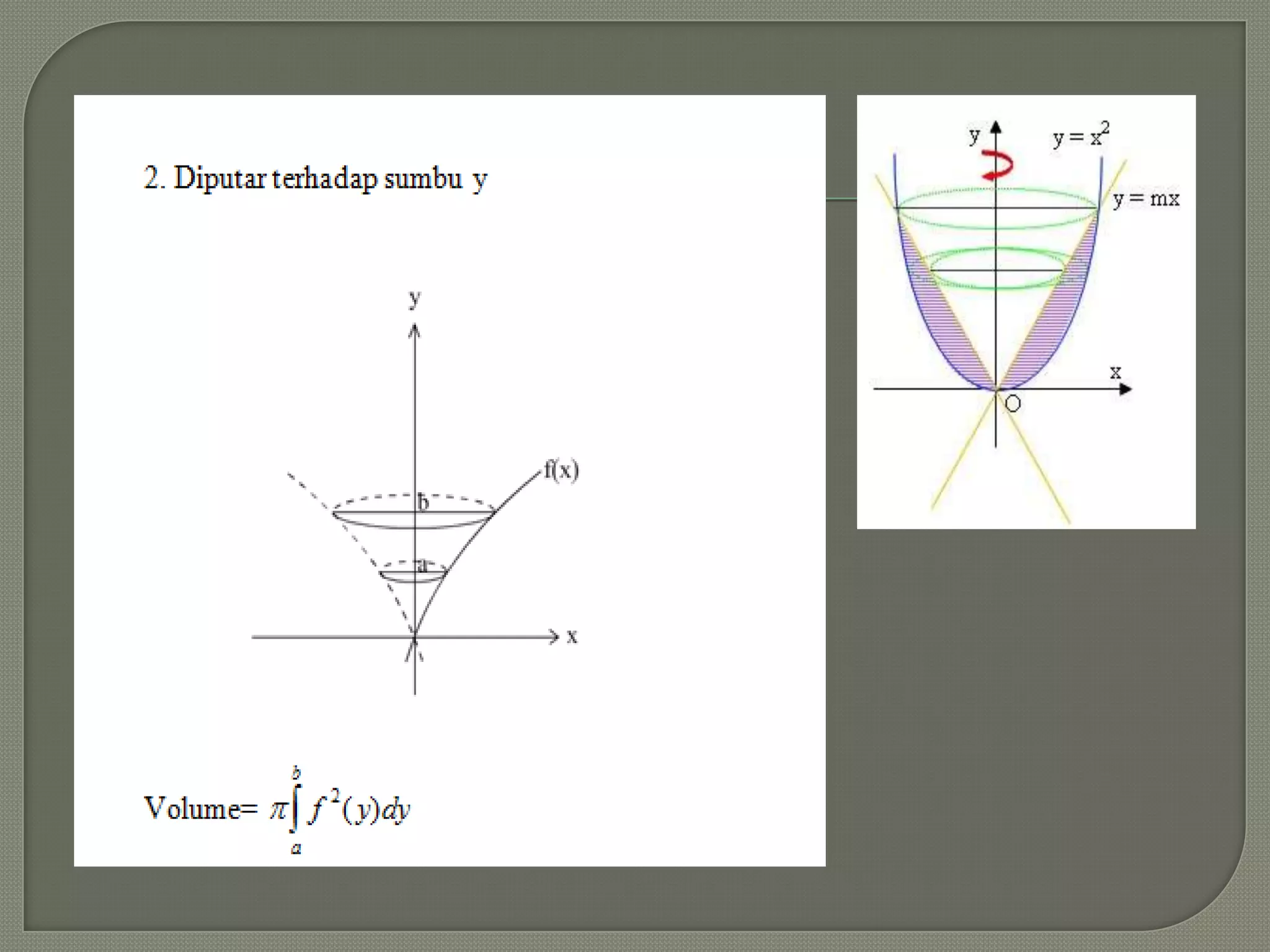
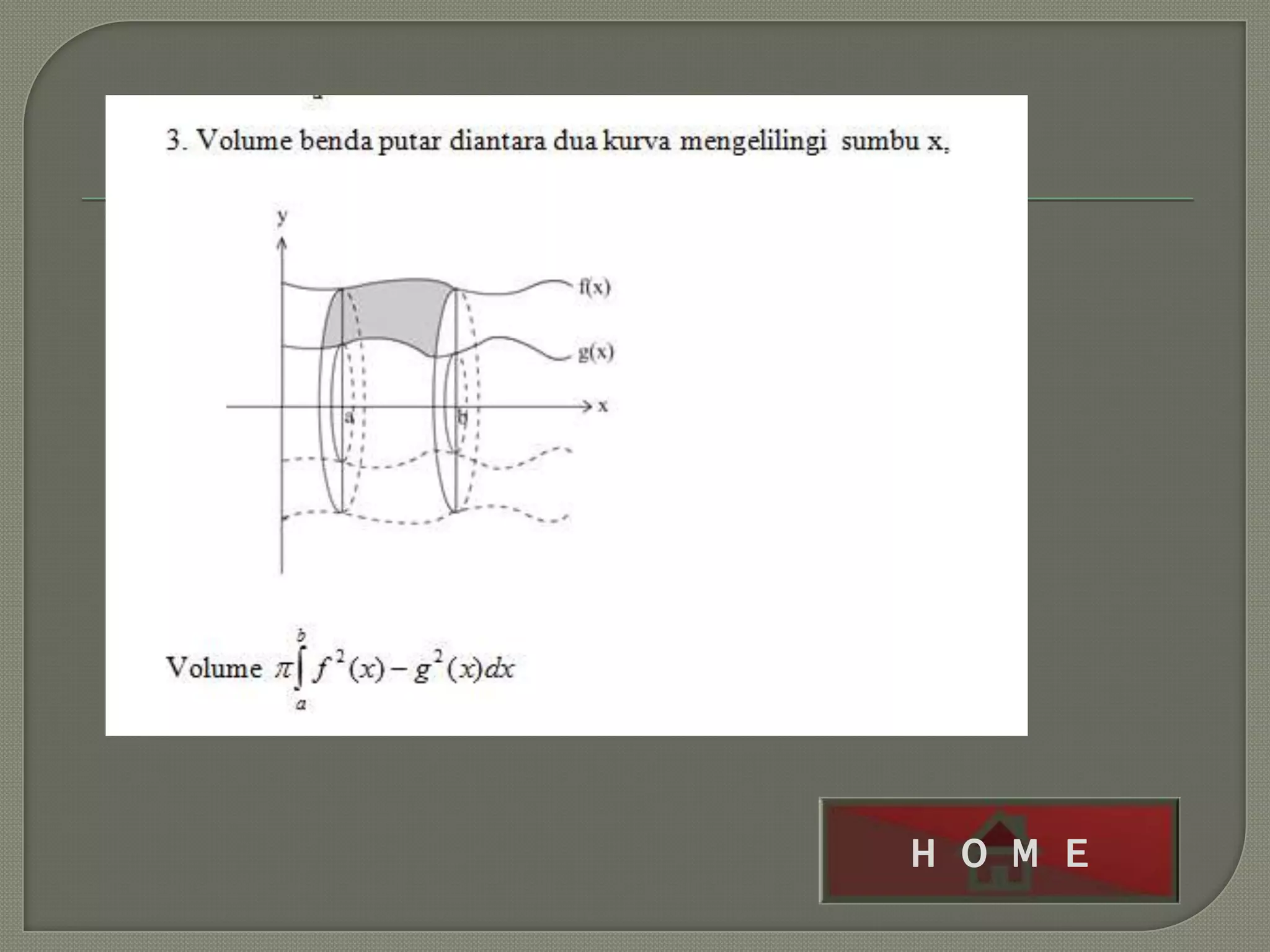
Dokumen tersebut membahas tentang integral dan aplikasinya dalam pembelajaran siswa SMA, mencakup pengertian integral tak tentu, integral tentu, dan integral parsial serta rumus dan prinsip dasarnya. Dokumen ini juga menjelaskan hubungan antara integral dengan turunan, luas daerah, dan contoh aplikasi integral dalam kehidupan sehari-hari.