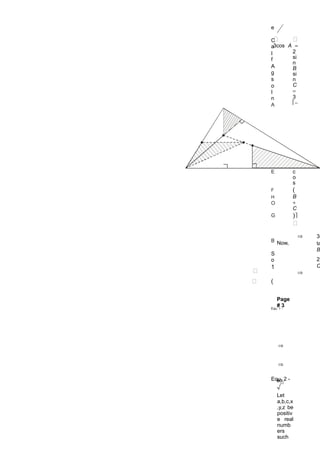
1. The triangle PQR is equilateral if the lines l1 and l2 intersecting at K satisfy KP = KQ. This is proved by showing that ∆KPO1O2 and ∆PQR are isosceles, with angles of 30 degrees, making ∆PQR equilateral. 2. The only positive integer solutions to m(4m^2 + m + 12) = 3(pn - 1) are m = 12, n = 4, p = 7. 3. The polynomial x^4 - ax^3 - bx^2 - cx - d cannot have an integer solution because its roots must be either integers or irrational in pairs, but

1. 28th Indian National Mathematical Olympiad-2013
Time : 4 hours Februray 03, 2013
Instructions :
• Calculators (in any form) and protractors are not allowed.
• Rulers and compasses are allowed.
• Answer all the questions. All questions carry equal marks.
• Answer to each question should start on a new page. Clearly indicate the questions number.
Let and Γ be two circles touching each other externally at R. Let be a line which is tangent to Γ
1. Γ l at
1 2 2
P and passing through the centre of Γ . Similarly, be a line which is tangent to Γ at Q and
O let l passing
2
1 1
through the centre of Γ . Suppose l are not parallel and intersect at K. If KP = KQ, prove that
O and l the
2 1
triangle PQR is equilateral.
Q P
K
O
1 R O2
Sol
.
KP = KQ, So K lies on the common tangent
(Radical Axis)
Now ∆ KPQ ~ ∆KO1O2 & PQK is isoceles
∠KQP = ∠KO1O2 
 PQO1O2 is cyclic 

∠KPQ = ∠KO2O1
So, ∆KO1O2 is also Isosceles So, KO1 = KO2 &
O1R = O2R, clearly in ∆O1PO2 ,
O1
PO2 O2
=
2
∠PO1O2 = 30º & similarly
so, ∠QO2O1 = 30º
∠O1KR = ∠O2KR = 60º & ∆PQR is
so, equilateral.

2. Page # 1
Find all positive integers m, n and primes p ≥ 5 such
2. that
m(4m2 + m + 12) = 3(pn – 1).
4
Sol m
. 3
+ m2 + 12m + 3 = 3pn
+
m 4m + 1 =
2 3 3pn
(
⇒ ) ; p ≥ 5 & prime
2
{so, m + 3 must be odd so m is even let m = 2a
4
a + 8a + 1 =
2
3 3pn
⇒ )
(
{Now a must be 3b or 3b + 1 because 3 is a factor so,
Case-1 - Let a = 3b
(36b2 + 3)(24b + 1) = 3pn
 (12b2 + 1)(24b + 1) = pn
Now 24b + 1 must divide 12b2 + 1 & hence it must divide b -
2, so the only possibility is b = 2 & hence m = 12 & p = 7, n =
4 Case-2 : if a = 3b + 1
 (36b2 + 24b + 7)(24b + 9) = 3pn
 (36b2 + 24b + 7)(8b + 3) = pn
2
+ 24b +
so, (8b + 3) must divide 36b 7
Hence divides 49 which is not possible for b ∈ Ι
m,n =
so, 12,4
( ) ( )
3. Let a,b,c,d be positive integers such that a ≥ b ≥ c ≥ d. Prove that the equation x4 – ax3 – bx2 – cx – d =
0 has no integer solution.
2
−
Sol a − bx − cx − d = 0 & a ≥ b ≥ c ≥
. x x d
a,b,c,d ∈ N
p
is
Let α be a factor of d because other roots can’t be of the
q as coefficient of
1
form x .
so, roots are either integers or unreal or irrational in pairs. Now there may be atleast one more
root (say β )which is integer & it is also a factor of d.

3. −d ≤ α,β
So, ≤d
}
Now, f 0 = −d < 0 & f −1 = 1+ a − b + c − d > 0
) ( )
f(x) < 0 for x ∈ , So there is no positive integral
also 0,d root.
[
Also. for x ∈ −d,−1 ; f(x) > 0 so, no integral root in [-d, -1].
[ ]
Hence there is no integral root. {Though roots are in (-1, 0)}.
4. Let n be a positive integer. Call a nonempty subset S of {1,2,3,.....,n} good if the arithemtic mean of the
elements of S is also an integer. Further let to denote the number of good subsets of {1,2,3,.....,n}.
Prove that tn and n are both odd or both even.
Let A = {x1, x2 , x3 ,...xr } be a good subset, then there must be
Sol
. a
B n − n −
n+1 + x + − x ,... n
= x, 1 , 1 +1 x
s { r } which is also good. So, good subsets occur in
e )
(
2
t ( ) (
) 3 ( ) a
pair.
However, there are few cases when A = B, which means if x ∈
A n + 1 − x ∈ A . To count the
⇒
i ( ) i
number of these subsets.
Case-1 : If n is odd.
a. If the middle element is excluded, the no. of elements in such subsets is 2k.
(k before middle, & k elements after). So sum of hte elements will be k(n + 1), Apparently these sets
n −1
are good. So no. of these subsets is 2 2 1(i.e. odd)
−
Page # 2

4. b. Similarly if mid term
these subsets will
good.
So number os sub
22
so toal number of s
2
5 S
. o
,
if
n
i
s
o
d
d
.
R
e
s
t
o
S f
t
o h
e
s
u
b
s
e
t
s
a
r
e
o
c
c
u
r
i
n
g
i
n
p
a
i
r
a
n
d
t
h
e
c
o
m
p
l
e
t

5. e
C  
a3cos A =
I 2
f si
n
A B
g si
s n
o C
I =
n 3
A −
E c
o
s
F (
H B
O +
C
G )

⇒ 3c
B Now,
ta
B
S
o 2s
1 C
 ⇒
 (
Page
#3
Equ. 1 -
⇒
⇒
Equ. 2 -
so,
Let
a,b,c,x
,y,z be
positiv
e real
numb
ers
such

6. t
h
Sol
.
Page
#4