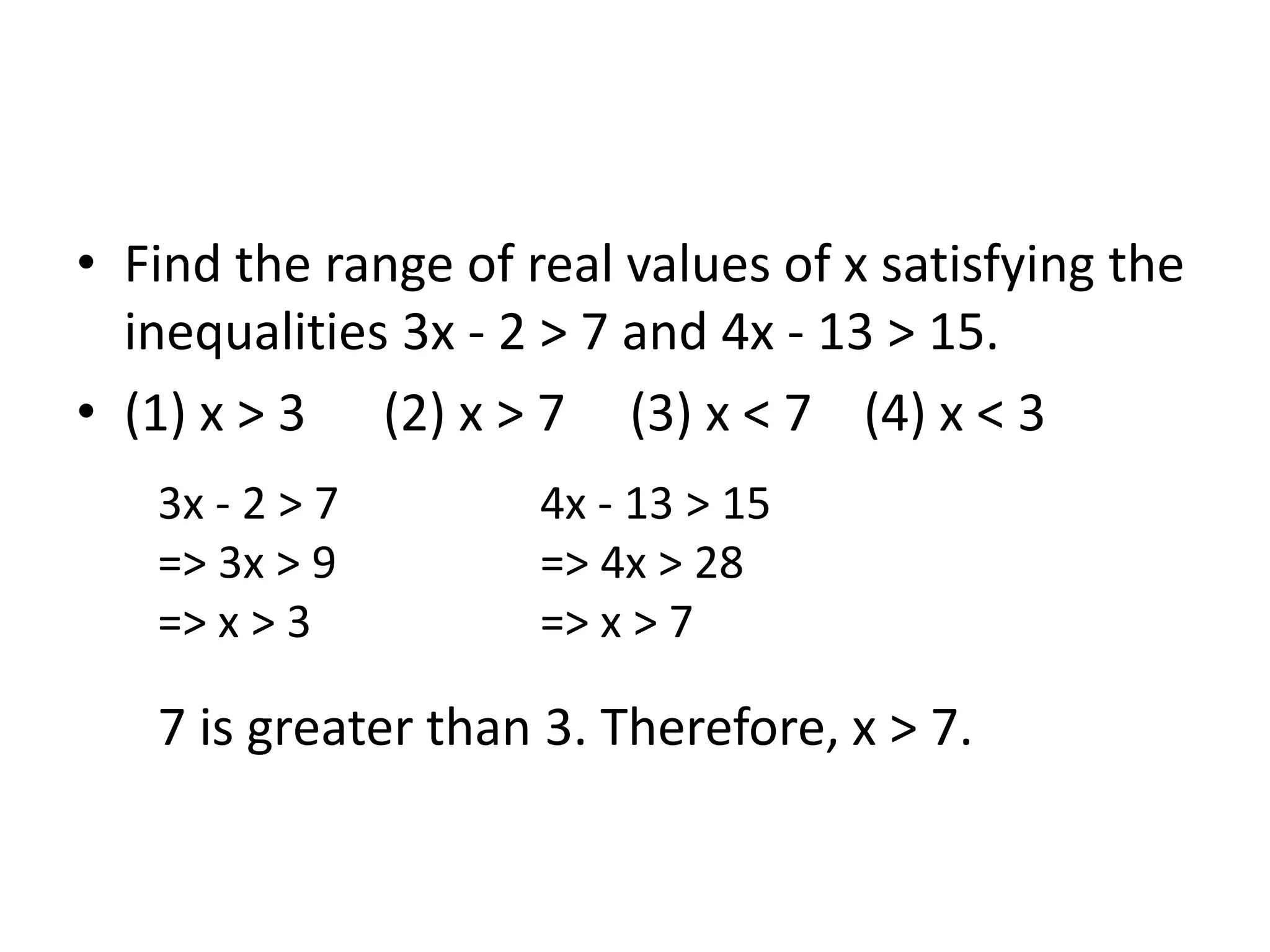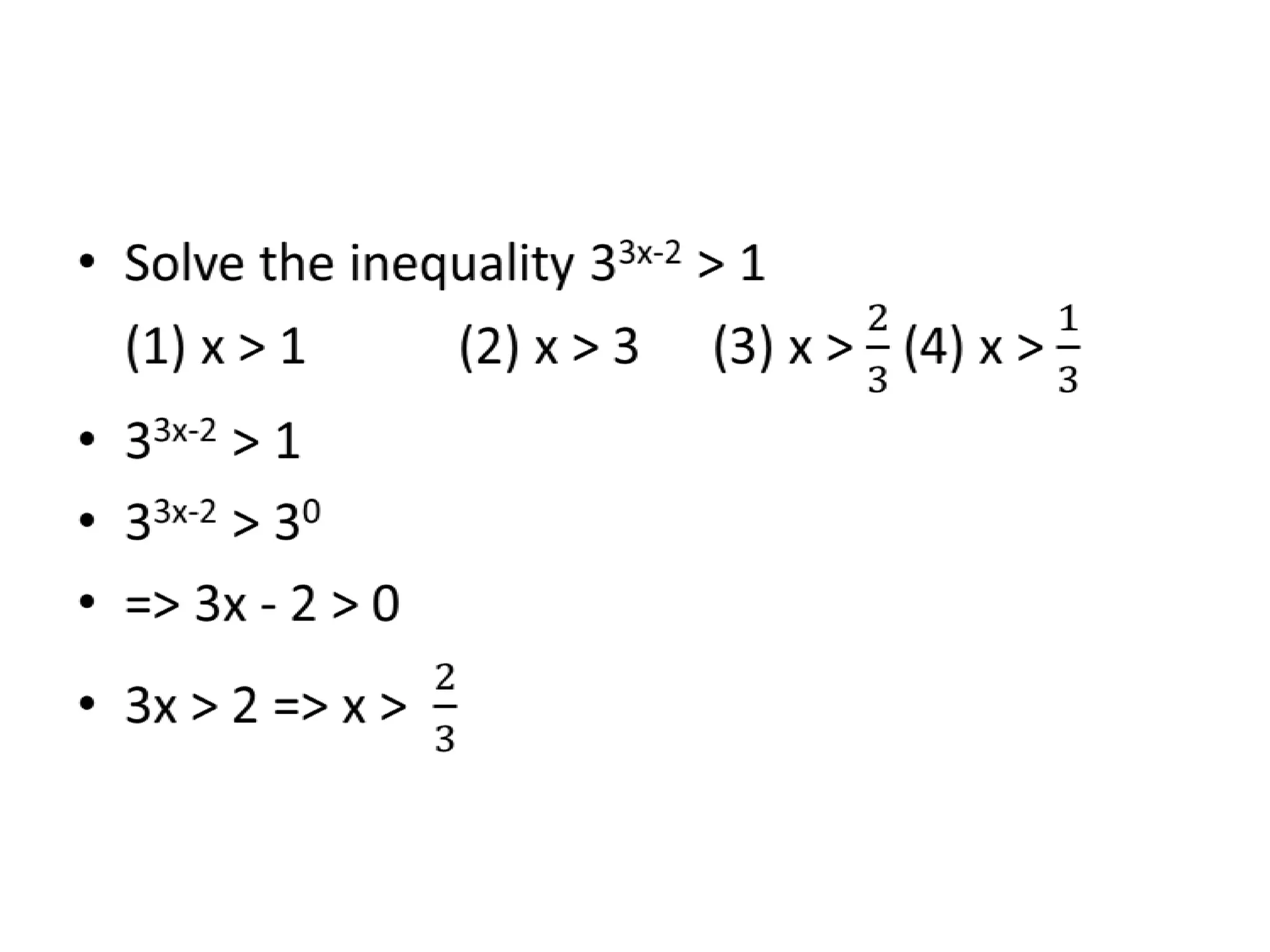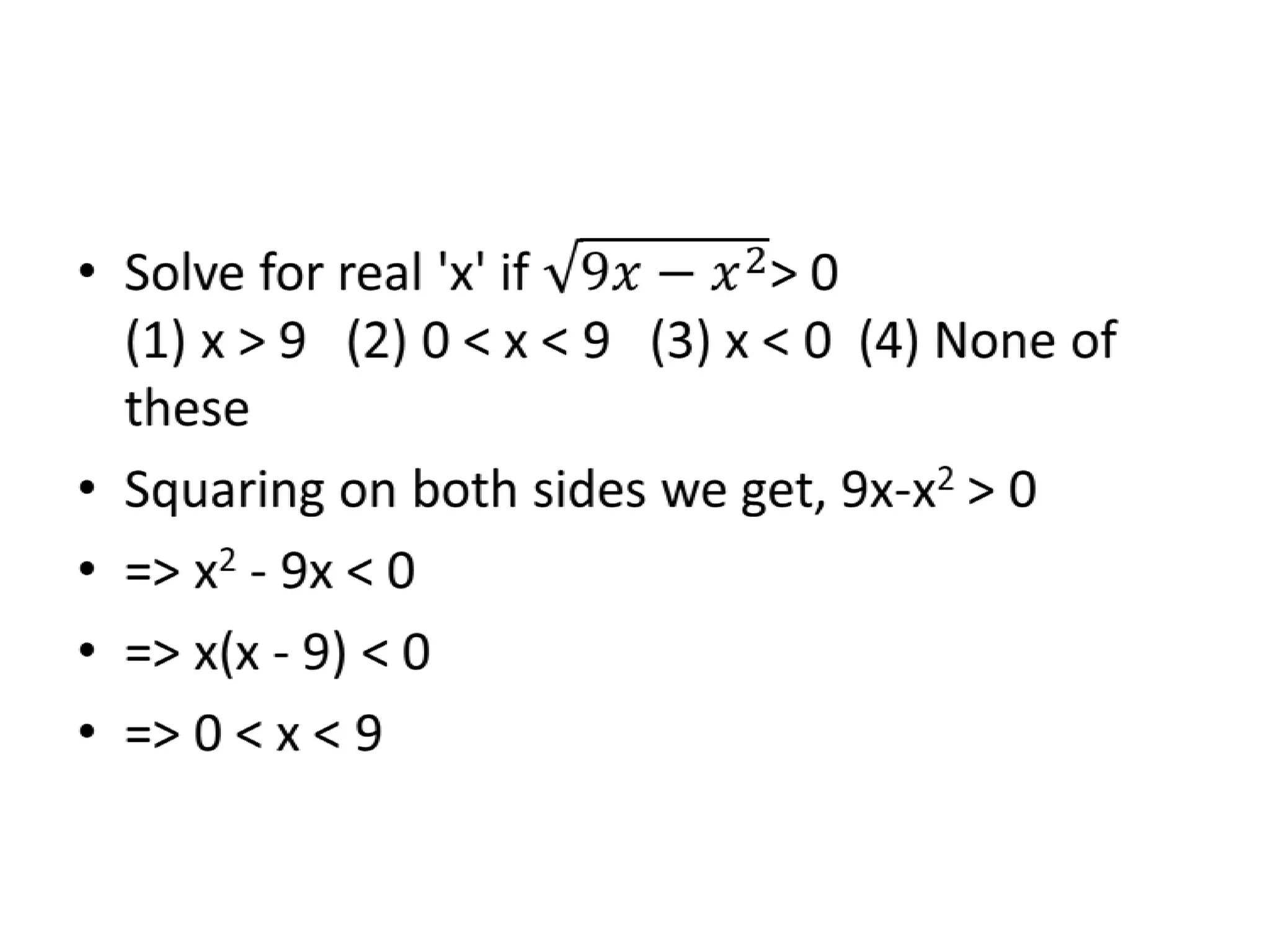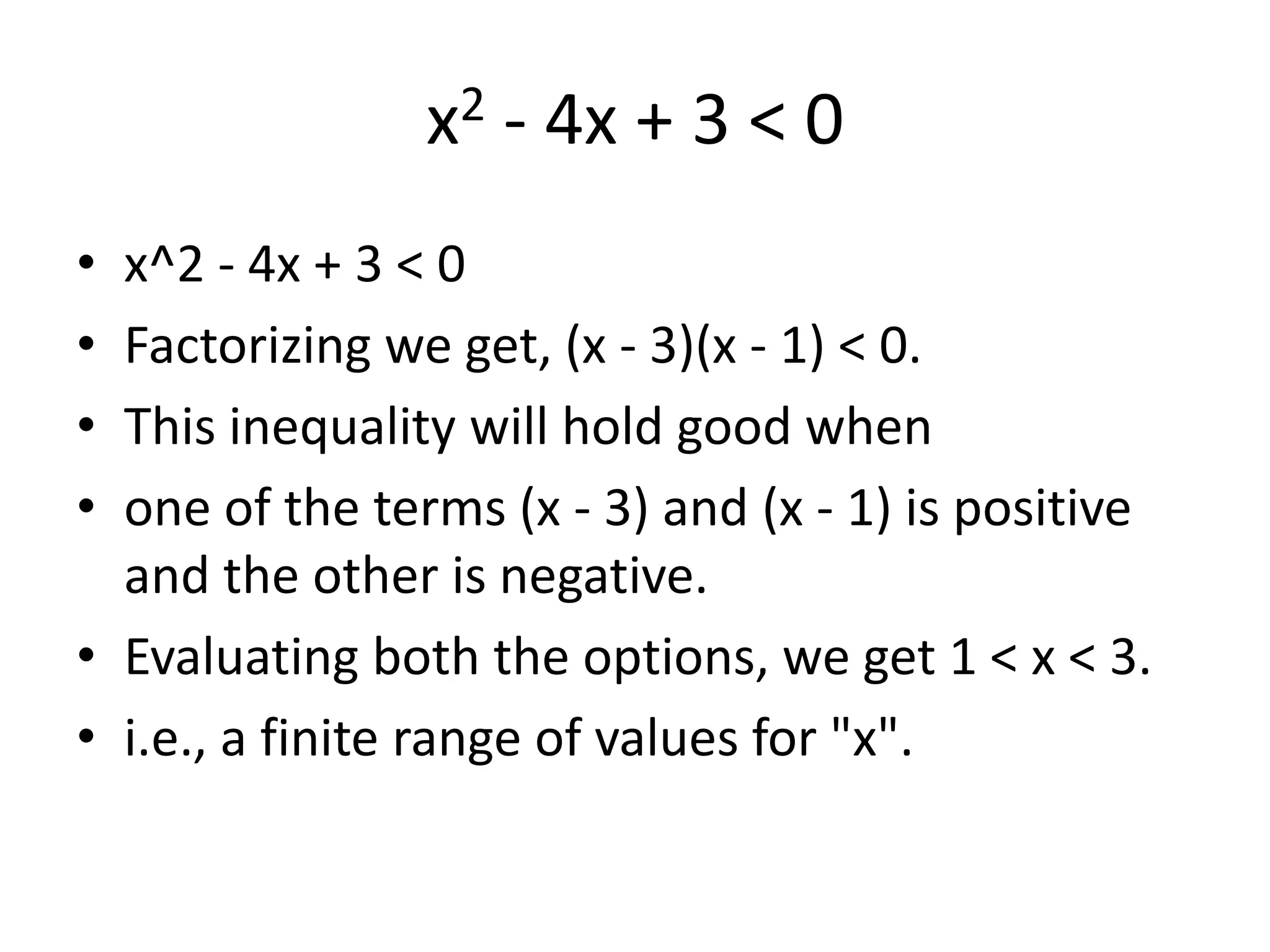The document discusses inequalities and modulus. It provides examples of determining the range of values for variables in different inequalities: 1) For the inequalities 3x - 2 > 7 and 4x - 13 > 15, the range of values is x > 7. 2) For the modulus inequality |x + 2| > 4, the range is infinite as x can be either less than -6 or greater than 2. 3) For the inequality x2 - 4x + 3 < 0, the range is finite between 1 and 3 as it is the only inequality that satisfies the condition of one term being positive and the other negative.

1. Inequalities and Modulus

2. • Find the range of real values of x satisfying the
inequalities 3x - 2 > 7 and 4x - 13 > 15.
• (1) x > 3 (2) x > 7 (3) x < 7 (4) x < 3
3x - 2 > 7
=> 3x > 9
=> x > 3
4x - 13 > 15
=> 4x > 28
=> x > 7
7 is greater than 3. Therefore, x > 7.

6. • Case 1:
• When both (x – 10) and (x + 4) are greater than or equal to 0.
• x > 10 and x > - 4 =>
• when x > 10 it will be greater than –4.
• Therefore, it will suffice to say that x > 10
• Case 2:
• When both (x - 10) and (x + 4) are less than or equal to 0.
• i.e. x < 10 and x < -4 => when x < -4, it will less than 10.
• Therefore, it will suffice to say that x < -4
• Hence, the range in which the given function will be defined in the
real domain will be when x does not lie between –4 and 10.

7. • Which of the following inequalities have a
finite range of values of "x" satisfying them?
• x2 + 5x + 6 > 0
• |x + 2| > 4
• 9x - 7 < 3x + 14
• x2 - 4x + 3 < 0
• Correct Answer - x2 - 4x + 3 < 0. Choice (4)

8. x2 + 5x + 6 > 0
• Factorizing the given equation, we get (x + 2)(x +
3) > 0.
• This inequality will hold good when
• both x + 2 and x + 3 are simultaneously positive
or simultaneously negative.
• Evaluating both the options, we get the range of
values of "x" that satisfy this inequality to be
• x < -2 or x > -3.
• i.e., "x" does not lie between -2 and -3 or an
infinite range of values.

9. |x + 2| > 4
• |x + 2| > 4 is a modulus function and therefore,
has two options
• Option 1: x + 2 > 4 or
• Option 2: (x + 2) < -4.
• Evaluating the two options we get the values of
"x" satisfying the inequality as
• x > 2 and x < -6.
• i.e., "x" does not lie between -6 and 2 or an
infinite range of values.

10. 9x - 7 < 3x + 14
• Simplifying, we get 6x < 21 or x < 3.5.
• Again an infinite range of values.

11. x2 - 4x + 3 < 0
• x^2 - 4x + 3 < 0
• Factorizing we get, (x - 3)(x - 1) < 0.
• This inequality will hold good when
• one of the terms (x - 3) and (x - 1) is positive
and the other is negative.
• Evaluating both the options, we get 1 < x < 3.
• i.e., a finite range of values for "x".