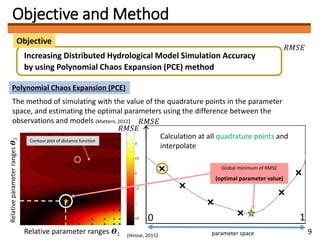
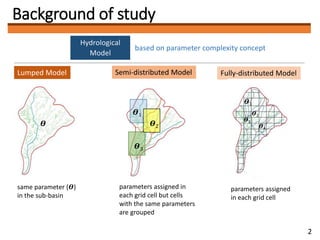
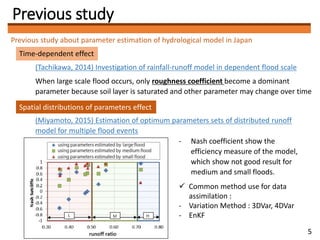
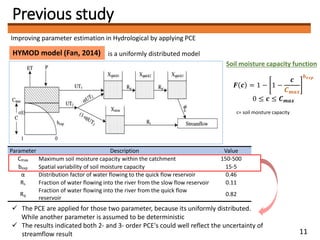
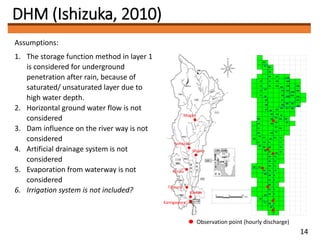
1) The document discusses applying the Polynomial Chaos Expansion (PCE) method to optimize parameters in distributed hydrological models and improve simulation accuracy. 2) PCE involves approximating a model output as a polynomial function of uncertain input parameters. It can efficiently estimate model outputs across the parameter space. 3) The author plans to use PCE to optimize soil-related parameters like layer thickness and hydraulic conductivity in a distributed hydrological model of the Ibo River catchment. Determining the optimal polynomial order for the model is a key future task.

1. M2 - Putika Ashfar Khoiri
Water Engineering Laboratory
Department of Civil Engineering
24th Cross-Boundary Seminar
International Program of Maritime and Urban Engineering
Osaka University
Improving Distributed Hydrological Model
Simulation Accuracy using Polynomial Chaos
Expansion (PCE)
*tentative title
December 21st, 2017

2. 1
Background of study
(Data from Japan Meteorological Agency)
 There is a change in precipitation
pattern due to climate change
 It is necessary to analyse rainfall-
runoff relationship to predict the
risk of flood and drought
increases due to climate change
 Perform hydrological model
Input
Hydrological
Model
Watershed
characteristics
Output river discharge
grid input set

3. 2
Background of study
based on parameter complexity concept
Hydrological
Model
Lumped Model
same parameter (𝜭)
in the sub-basin
Semi-distributed Model
parameters assigned in
each grid cell but cells
with the same parameters
are grouped
𝜭
𝜭1
𝜭2
𝜭3
Fully-distributed Model
parameters assigned
in each grid cell
𝜭1
𝜭2
𝜭3
𝜭4

4. 3
Background of study
based on parameter complexity concept
Hydrological
Model
Fully-distributed Model
parameters assigned
in each grid cell
Advantages
1. Can consider the spatial distribution of input
2. Can predict output discharge at any point
Disadvantage
1. Require many parameters so the setting and
determination of parameter is difficult
We need to assess the effectiveness of distributed
parameter including the characteristics of every
parameter
Parameter optimization is required to decrease the
uncertainty
Approach:
𝜭1
𝜭2
𝜭3
𝜭4

5. Approach
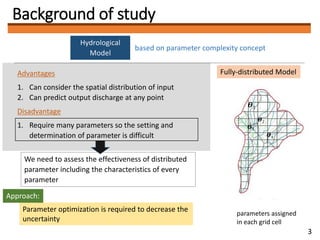
 In order to optimize the poorly known parameters and improve the model forecast
ability, data assimilation is required
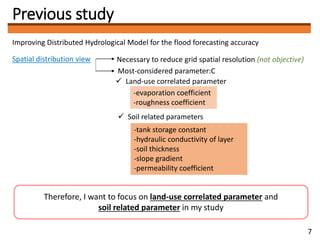
Input and/or parameters
Uncertain characterisation
𝑥 = [𝑥1, 𝑥2, … … . . 𝑥 𝑛]
System simulation
• Process
• Equations
• Code
𝑦 = 𝑓(𝑥)
Outputs
𝑦 = [𝑦1, 𝑦2, … … . . 𝑦 𝑛]
- Parameter optimization
- Sensitivity analysis
- Distribution statistics
- Performance measures
(variance, RMSE)
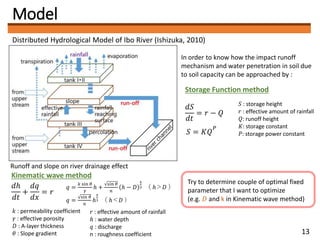
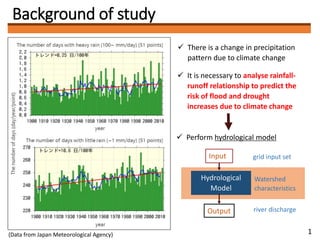
 Characterization of uncertainty in hydrologic models is often critical for many water
resources applications (drought/ flood management, water supply utilities, reservoir
operation, sustainable water management, etc.).
4

6. Previous study
Previous study about parameter estimation of hydrological model in Japan
Time-dependent effect
(Tachikawa, 2014) Investigation of rainfall-runoff model in dependent flood scale
When large scale flood occurs, only roughness coefficient become a dominant
parameter because soil layer is saturated and other parameter may change over time
Spatial distributions of parameters effect
(Miyamoto, 2015) Estimation of optimum parameters sets of distributed runoff
model for multiple flood events
- Nash coefficient show the
efficiency measure of the model,
which show not good result for
medium and small floods.
5
 Common method use for data
assimilation :
- Variation Method : 3DVar, 4DVar
- EnKF

7. Previous study
Improving Hydrological Model response based on the soil types, land-uses and slope
classes
Example : Soil and Water Assessment Tool (SWAT) model
The turning of parameters is difficult because so many parameter need to be considered ->
sensitivity analysis is needed
𝑆𝑊𝑡 = 𝑆𝑊0 +
𝑖=1
𝑡
(𝑅 𝑑𝑎𝑦 + 𝑄𝑠𝑢𝑟𝑓 + 𝐸 𝑎 − 𝑤𝑠𝑒𝑒𝑝 − 𝑄 𝑔𝑤)
Uncertainty analysis methods
e.g. GLUE (Generalized Likelihood Method Uncertainty Estimation) ,
based on Monte-Carlo simulation
Problem -> Need large number of parameter sets sample
SWt = final soil water content
SW0 = initial soil water content on day i
Rday = amount of precipitation on day i
Qsurf = amount of surface runoff on day i
Ea = amount of evatranspiration on day i
Wseep = amount of water entering the vadose zone from the soil
Qgw = amount of water return flow on day i
6

8. Previous study
Improving Distributed Hydrological Model for the flood forecasting accuracy
Spatial distribution view Necessary to reduce grid spatial resolution (not objective)
 Land-use correlated parameter
Most-considered parameter:C
 Soil related parameters
-evaporation coefficient
-roughness coefficient
-tank storage constant
-hydraulic conductivity of layer
-soil thickness
-slope gradient
-permeability coefficient
Therefore, I want to focus on land-use correlated parameter and
soil related parameter in my study
7

9. Objective and Method
Polynomial Chaos Expansion (PCE)
𝑓 𝑥, 𝑡, 𝜃 =
𝑘=0
𝑘 𝑚𝑎𝑥
𝑎 𝑘(𝑥, 𝑡) 𝜙 𝑘(𝜃)
𝑏𝑎𝑠𝑖𝑐 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑝𝑜𝑙𝑦𝑛𝑜𝑚𝑖𝑎𝑙
Any model output Expansion
coefficient
Polynomial of
order-k in
parameter space
determined by 𝜃
𝑎 𝑘 𝑥, 𝑡 =
1
𝑁𝑘
𝑓 𝑥, 𝑡, 𝜃 𝜙 𝑘 𝜃 𝑝 𝜃 𝑑(𝜃)
Density function
of parameter 𝜃
approximate by
Gaussian
Quadrature
(Mattern, 2012)
PCE has used to
optimize
parameter on
biological ocean
model
8

10. Objective and Method
Polynomial Chaos Expansion (PCE)
Increasing Distributed Hydrological Model Simulation Accuracy
by using Polynomial Chaos Expansion (PCE) method
Objective
The method of simulating with the value of the quadrature points in the parameter
space, and estimating the optimal parameters using the difference between the
observations and models (Mattern, 2012)
𝑅𝑀𝑆𝐸が最小
parameter space
Calculation at all quadrature points and
interpolate
𝑅𝑀𝑆𝐸
0 1
𝑅𝑀𝑆𝐸
2 4 6 8 10
x 10
-3
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
parameter: KDOMf
parameter:ratio_n
0.5
1
1.5
2
2.5
3
𝑅𝑀𝑆𝐸
Relative parameter ranges 𝜭1
Relativeparameterranges𝜭2
Global minimum of RMSE
(optimal parameter value)
Contour plot of distance function
(Hirose, 2015) 9

11. Method (PCE)
Emulator techniques
Polynomial Chaos Expansion (PCE)
Advantages:
- More effective than Monte-Carlo
because of their random sampling
- PCE performs a polynomial interpolation
in parameter space so it can estimate
any model output for the parameter
value of choice
Challenges:
- We must know what kind of input
parameters that make large uncertainty
- Upper and lower limits of parameter is
difficult to set
- Only two parameters can be optimized
We need to carefully consider:
1. Uncertain model input (parameters)
2. The prior distributions assigned to these
input
3. kmax (max. order of polynomial) -> we
have to check which value of kmax is
applicable for DHM
10

12. Previous study
Improving parameter estimation in Hydrological by applying PCE
HYMOD model (Fan, 2014) is a uniformly distributed model
Parameter Description Value
Cmax Maximum soil moisture capacity within the catchment 150-500
bexp Spatial variability of soil moisture capacity 15-5
α Distribution factor of water flowing to the quick flow reservoir 0.46
Rs Fraction of water flowing into the river from the slow flow reservoir 0.11
Rq
Fraction of water flowing into the river from the quick flow
reservoir
0.82
Soil moisture capacity function
c= soil moisture capacity
𝑭 𝒄 = 1 − 1 −
𝒄
𝑪 𝒎𝒂𝒙
𝒃 𝒆𝒙𝒑
0 ≤ 𝒄 ≤ 𝑪 𝒎𝒂𝒙
 The PCE are applied for those two parameter, because its uniformly distributed.
While another parameter is assumed to be deterministic
 The results indicated both 2- and 3- order PCE's could well reflect the uncertainty of
streamflow result 11

13. Previous study
PCE method for HYMOD model (Fan, 2014)
12

14. Model
Distributed Hydrological Model of Ibo River (Ishizuka, 2010)
In order to know how the impact runoff
mechanism and water penetration in soil due
to soil capacity can be approached by :
Storage Function method
𝑑𝑆
𝑑𝑡
= 𝑟 − 𝑄
𝑆 = 𝐾𝑄
𝑃
𝑆 : storage height
𝑟 : effective amount of rainfall
𝑄: runoff height
𝐾: storage constant
𝑃: storage power constant
Runoff and slope on river drainage effect
Kinematic wave method
𝑑ℎ
𝑑𝑡
+
𝑑𝑞
𝑑𝑥
= 𝑟
𝑞 =
𝑘 sin 𝜃
𝛾
ℎ +
sin 𝜃
𝑛
ℎ − 𝐷
5
3 （ ℎ＞𝐷 ）
𝑞 =
sin 𝜃
𝑛
ℎ
5
3 （ ℎ＜𝐷 ）
𝑟 : effective amount of rainfall
ℎ : water depth
𝑞 : discharge
n : roughness coefficient
Try to determine couple of optimal fixed
parameter that I want to optimize
(e.g. 𝐷 and k in Kinematic wave method)
𝑘 : permeability coefficient
𝛾 : effective porosity
𝐷 : A-layer thickness
𝜃 : Slope gradient 13

15. DHM (Ishizuka, 2010)
Assumptions:
1. The storage function method in layer 1
is considered for underground
penetration after rain, because of
saturated/ unsaturated layer due to
high water depth.
2. Horizontal ground water flow is not
considered
3. Dam influence on the river way is not
considered
4. Artificial drainage system is not
considered
5. Evaporation from waterway is not
considered
6. Irrigation system is not included?
Magari
Yamazaki
Shiono
Kurisu
Tatsuno
Kamigawara
Kamae
Observation point (hourly discharge)
14

16. Method (Apply PCE to DHM)
Candidate for parameter optimization which are related to storage
capacity of water in the soil (Ishizuka, 2010)
Runoff on slope and river channel
Description Parameter Value
slope gradient θ 0.01-13.5
roughness coefficient n 0.01-2
layer A thickness D 200
effective porosity of layer A γ 0.2
hydraulic conductivity of layer A k 0.3
distance difference ∆x 20
time interval ∆t 0.001
storage constant of tank I K1 3.2
storage constant of tank II K2 14
(Note : The range of value for each parameter should be discussed to avoid many trial and error)
15
1. Try to apply PCE to soil capacity related parameter within the catchment in
the first layer refer to Kinematic Wave equation
2。Therefore, it is necessary to check which value of polynomial order (k) is
applicable to this model

17. Future task
16
Test the D and k parameter with PCE to select suitable and optimum
value for the polynomial order (k) within single flood event
Determine time range for the single flood event
 Study MATLAB to make modification on PCE code, apply on DHM model
Convert D and k parameter to Gaussian variables