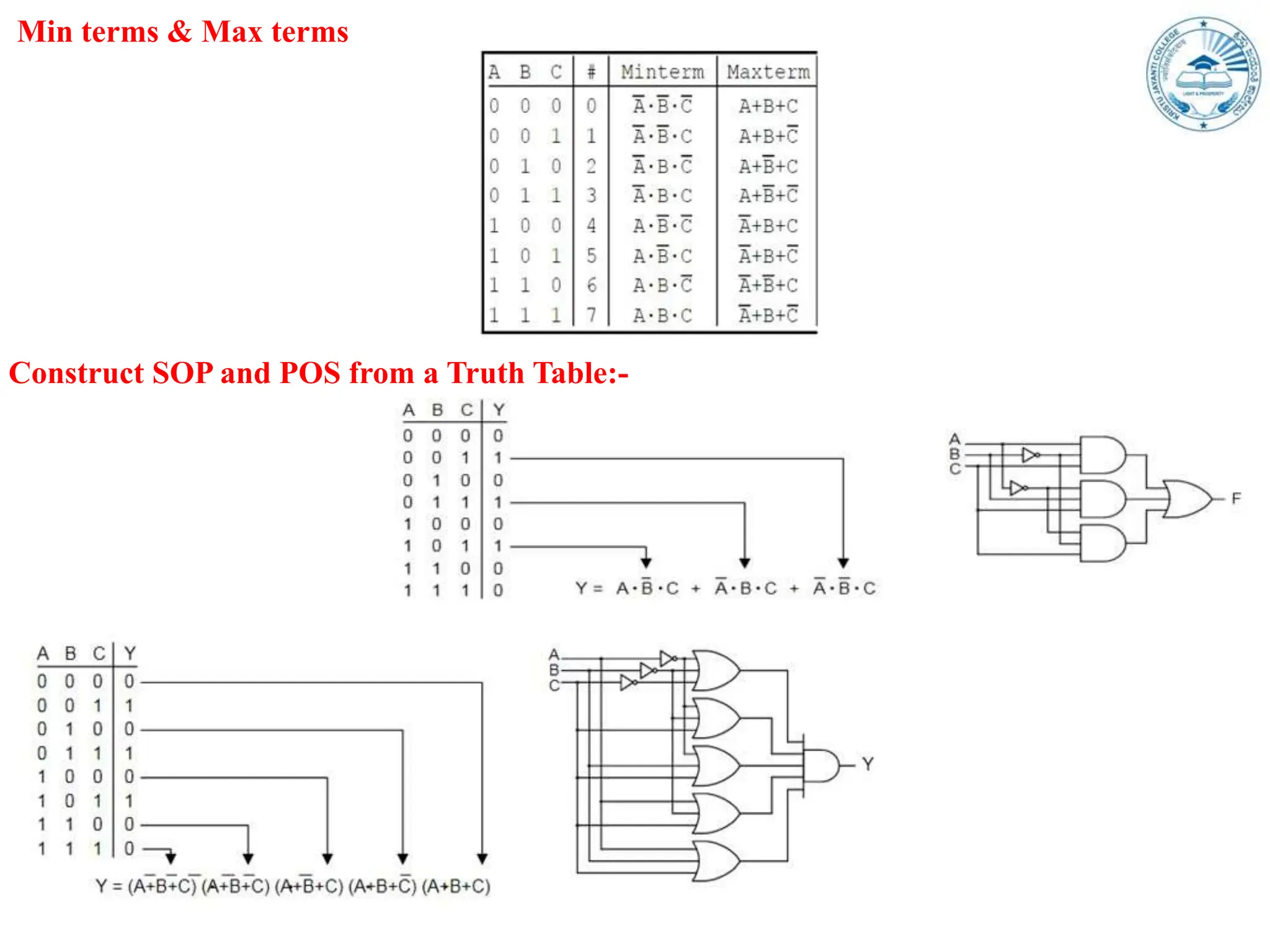
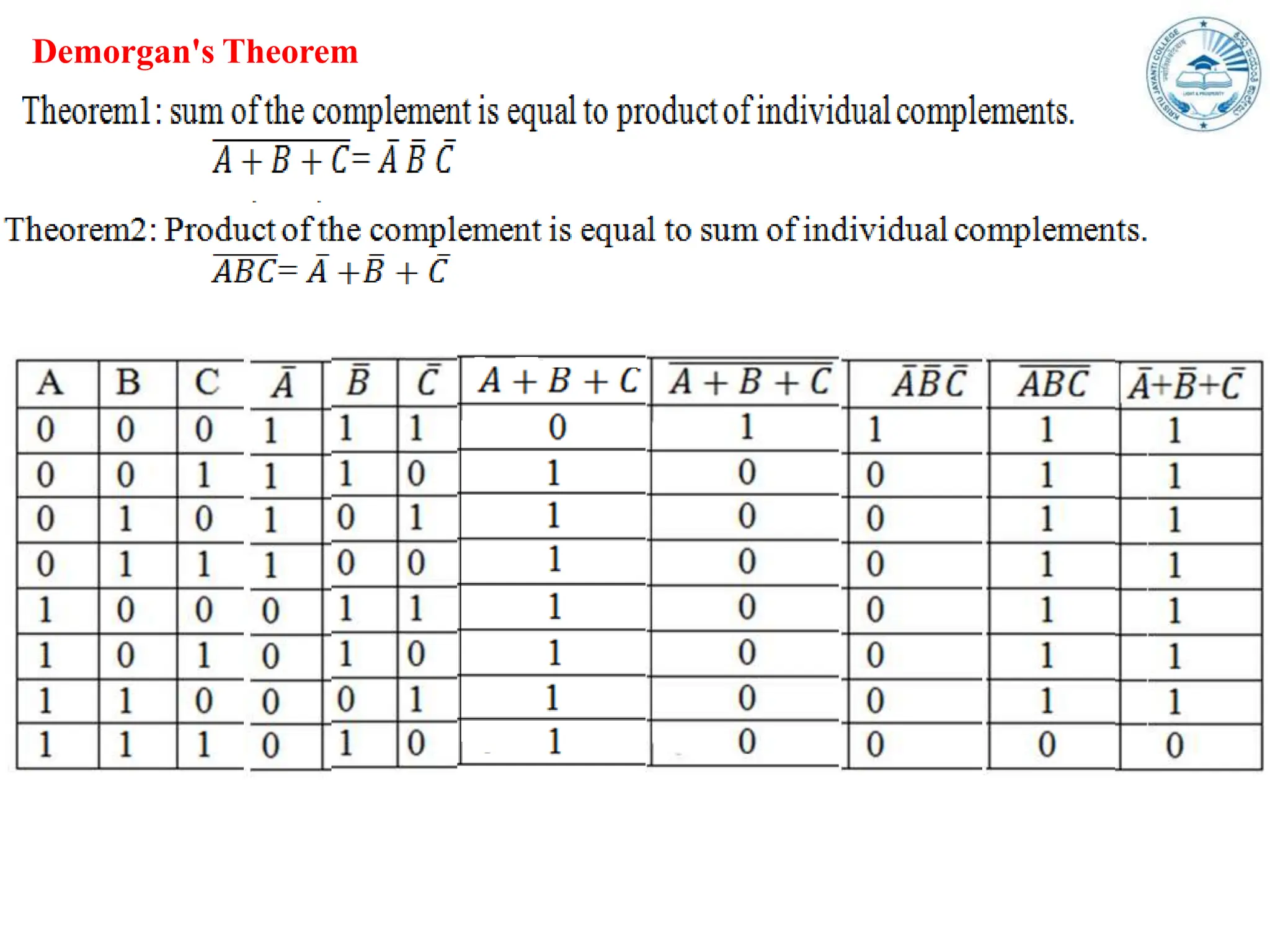
Boolean expressions use variables, constants, and logical operators to evaluate to true or false. They can be expressed in Sum-of-Products (SOP) form or Product-of-Sums (POS) form, and are classified as canonical (standard) SOP or POS. Canonical forms have each term containing all variables. SOP represents the function as a sum of product terms, while POS is the opposite as a product of sum terms. Boolean expressions are also represented using truth tables, min/max terms, Demorgan's theorem, and derived gates.

2. A Boolean expression is an expression which consists of variables, constants
and logical operators which results in true or false.
Boolean Functions/expression:-
• Sum-of-Products (SOP) Form
• Product-of-sums (POS) form
• Canonical forms
Boolean expressions are classified as
• Sum-of-min terms or Canonical SOP
• Product-of- max terms or Canonical POS
Canonical forms are further classified as

3. Sum Of Product (SOP) Form:-
In this SOP form of Boolean function representation, the variables are operated by AND
(product) to form a product term and all these product terms are ORed (summed or
added) together to get the final function.
Example:
In this POS form, all the variables are ORed, All these sum terms are ANDed (multiplied)
together to get the product-of-sum form. This form is exactly opposite to the SOP form. So
this can also be said as “Dual of SOP form”.
Product Of Sum (POS) Form:-
Example:

4. Canonical Form (Standard SOP and POS) Form:-
Any Boolean function is said to be in its canonical form if each term in the
expression contains all the variables.
A minterm is defined as the product term of n variables in Sum Of Product (SOP)
expression, in which each of the n variables will appear once either in its complemented or
un-complemented form. The min term is denoted as mi
Min terms
A max term is defined as the sum term of n variables in Product Of Sum (SOP) expression,
in which each of the n variables will appear once either in its complemented or un-
complemented form. The max term is denoted as Mi.
Max terms

5. Min terms & Max terms
Construct SOP and POS from a Truth Table:-

6. Demorgan's Theorem

9. Derived gates