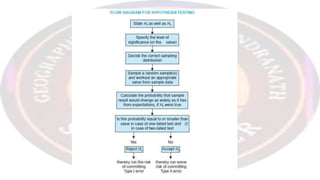
The document provides an in-depth overview of research hypotheses, including definitions, components, types, and the formulation and testing processes. It highlights important aspects such as the null and alternative hypotheses, statistical tests, and limitations of hypothesis testing like sample size and p-value misinterpretation. The document emphasizes the need for clear research questions and the ethical considerations involved in hypothesis testing.

1. HYPOTHESIS?
DR.NARENDRANATH

2. • Introduction to Research Hypothesis
• Components of a Hypothesis
• Types of Hypotheses
• Formulating a Hypothesis
• Testing a Hypothesis

3. What is a Hypothesis?
• Definition: A hypothesis is a statement that
suggests a relationship between variables.
• Purpose: It serves as the basis for research,
guiding investigation and testing.

4. Components of a Hypothesis
• Independent Variable (IV)
• Dependent Variable (DV)
• Null Hypothesis (H0)
• Alternative Hypothesis (Ha or H1)

5. Types of Hypotheses
• Null Hypothesis (H0): Suggests no significant
relationship or effect.
• Alternative Hypothesis (Ha or H1): Proposes a
specific relationship or effect.

6. Characteristics of hypothesis
Testable:
Falsifiable:
Clear and Specific:
Based on Prior
Knowledge:
Empirical:
Logical and Rational:
Predictive:
Alternative and Null
Hypotheses:
Measurable
Subject to Revision:
Independent and Dependent
Variables
Ethical Considerations
Contextual Awareness
Hypothesis Statement

7. TESTING OF HYPOTHESES
• (a) Null hypothesis and alternative hypothesis:
• (b) The level of significance:
• (c) Decision rule or test of hypothesis:
• (d) Type I and Type II errors:
• (e) Two-tailed and One-tailed tests:

8. PROCEDURE FOR HYPOTHESIS TESTING
• (i) Making a formal statement:
• (ii) Selecting a significance level:
• (iii) Deciding the distribution to use:
• (iv) Selecting a random sample and computing
an appropriate value:
• (v) Calculation of the probability:
• (vi) Comparing the probability:

9. Formulating a Hypothesis
• Begin with a clear research question.
• Identify the variables (IV and DV).
• State the null hypothesis (H0).
• State the alternative hypothesis (Ha or H1).
• Ensure it's testable and specific.

11. IMPORTANT PARAMETRIC TESTS
The important parametric tests are:
(1) z-test; (2) t-test; (3) X2-test, and (4) F-test

12. Testing a Hypothesis
• Design your research study.
• Collect data.
• Analyze data using appropriate statistical
methods.
• Determine whether to accept or reject the
null hypothesis based on evidence.

13. • Examples
• Example 1: Relationship between tutoring and test scores.
– H0: There is no significant difference in test scores between students who
receive tutoring and those who do not.
– Ha: Students who receive tutoring will achieve higher test scores than
those who do not.
• Example 2: Effect of a new drug on patient recovery time.
– H0: The new drug has no significant effect on patient recovery time.
– Ha: The new drug reduces patient recovery time compared to the old
drug.

14. LIMITATIONS OF THE TESTS OF
HYPOTHESES

15. 
Simplification of Reality: Hypothesis testing often involves
simplifying complex real-world situations into manageable models.
This simplification may not fully capture the nuances of the
phenomenon being studied, leading to an oversimplified
representation.
 Assumptions: Many hypothesis tests rely on assumptions about the
data, such as the normality of the distribution or the homogeneity
of variances. If these assumptions are violated, the results of the
test may be unreliable.
 Sample Size: The power of a hypothesis test (the ability to detect a
true effect) is often influenced by the sample size. Small sample
sizes may not provide enough statistical power to detect real effects,
leading to false negative results.

16. • Type I and Type II Errors: Hypothesis testing involves a trade-off
between Type I errors (false positives) and Type II errors (false
negatives). Controlling one type of error can increase the
likelihood of the other, making it challenging to find a balance.
• P-Value Misinterpretation: Misinterpretation of p-values is
common. Researchers sometimes mistakenly believe that a
small p-value implies the practical significance or importance of
an effect, which is not necessarily the case.
• Publication Bias: Research that produces statistically significant
results is more likely to be published, while studies with non-
significant findings may remain unpublished. This can lead to a
skewed representation of the literature and overestimate the
true effect size.

17. • Multiple Comparisons: Conducting multiple hypothesis tests on the
same data can increase the likelihood of finding significant results
purely by chance. This problem is often addressed by using methods
like Bonferroni correction, but it can still be a concern.
• Generalizability: Findings from hypothesis tests may not always
generalize to other populations or settings. It's essential to consider
the external validity of the results.
• Biased Data: If the data used for hypothesis testing is biased or not
representative of the population of interest, the results may not be
applicable beyond the sample.
• Ethical and Practical Constraints: In some cases, ethical or practical
constraints may limit the ability to conduct controlled experiments or
collect data in a way that aligns perfectly with the hypothesis testing
framework

18. • Complex Causality: Hypothesis testing often focuses
on establishing relationships between variables, but
many real-world phenomena involve complex
causality with multiple factors influencing outcomes.
Hypothesis tests may oversimplify these situations.
• Interactions and Context: Hypothesis tests may not
account for interactions between variables or the
broader context in which the phenomenon occurs.
This can lead to incomplete or misleading
conclusions.

19. • It's important to recognize these limitations
when using hypothesis testing in research and
to complement hypothesis testing with other
research methods when necessary to gain a
more comprehensive understanding of a topic.
Additionally, transparent reporting of methods
and results can help mitigate some of these
limitations.