Suzanne Wallace, profile picture
Uploaded bySuzanne Wallace
PPTX, PDF410 views

Hoffmann band structures JC talk

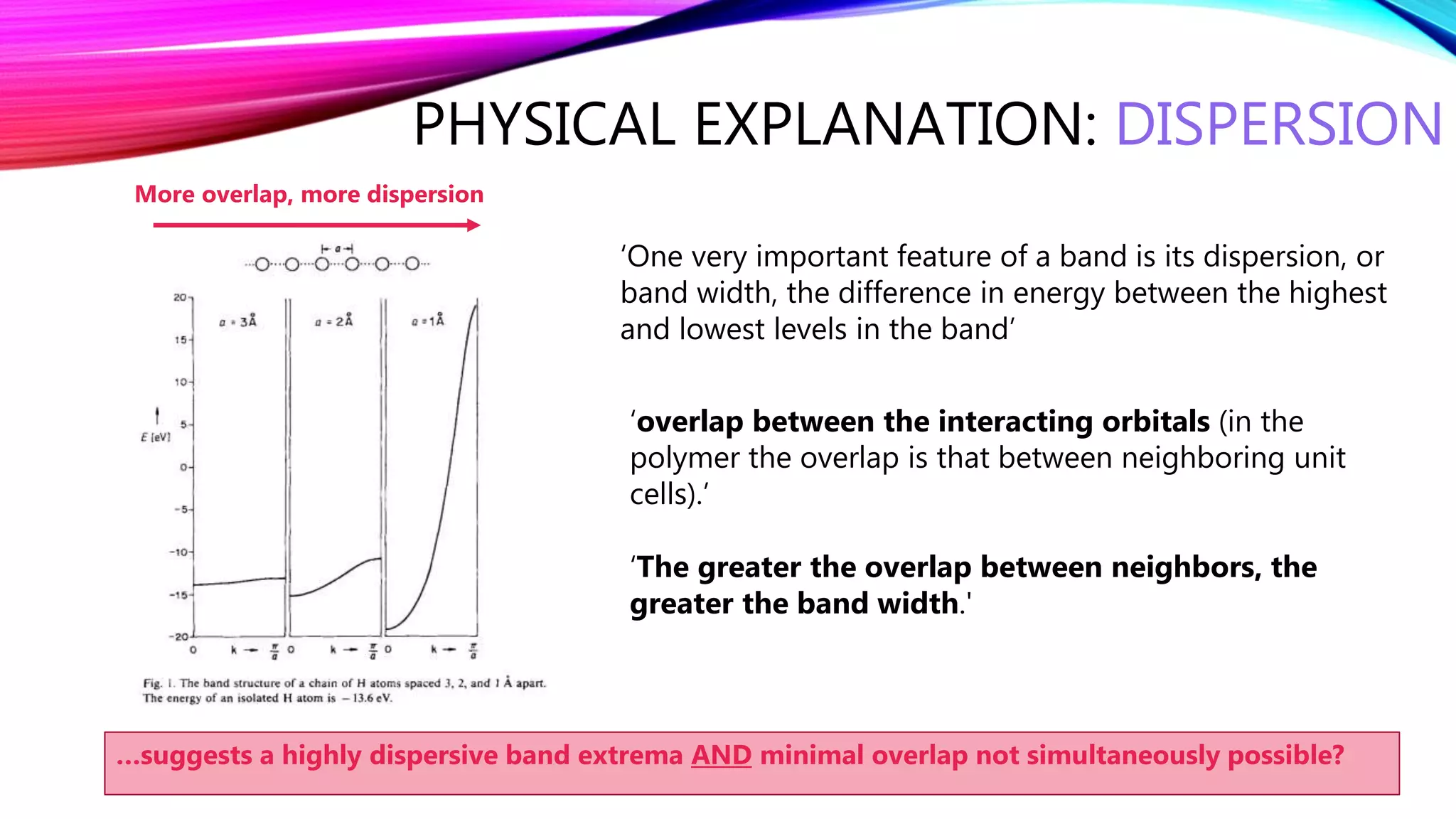
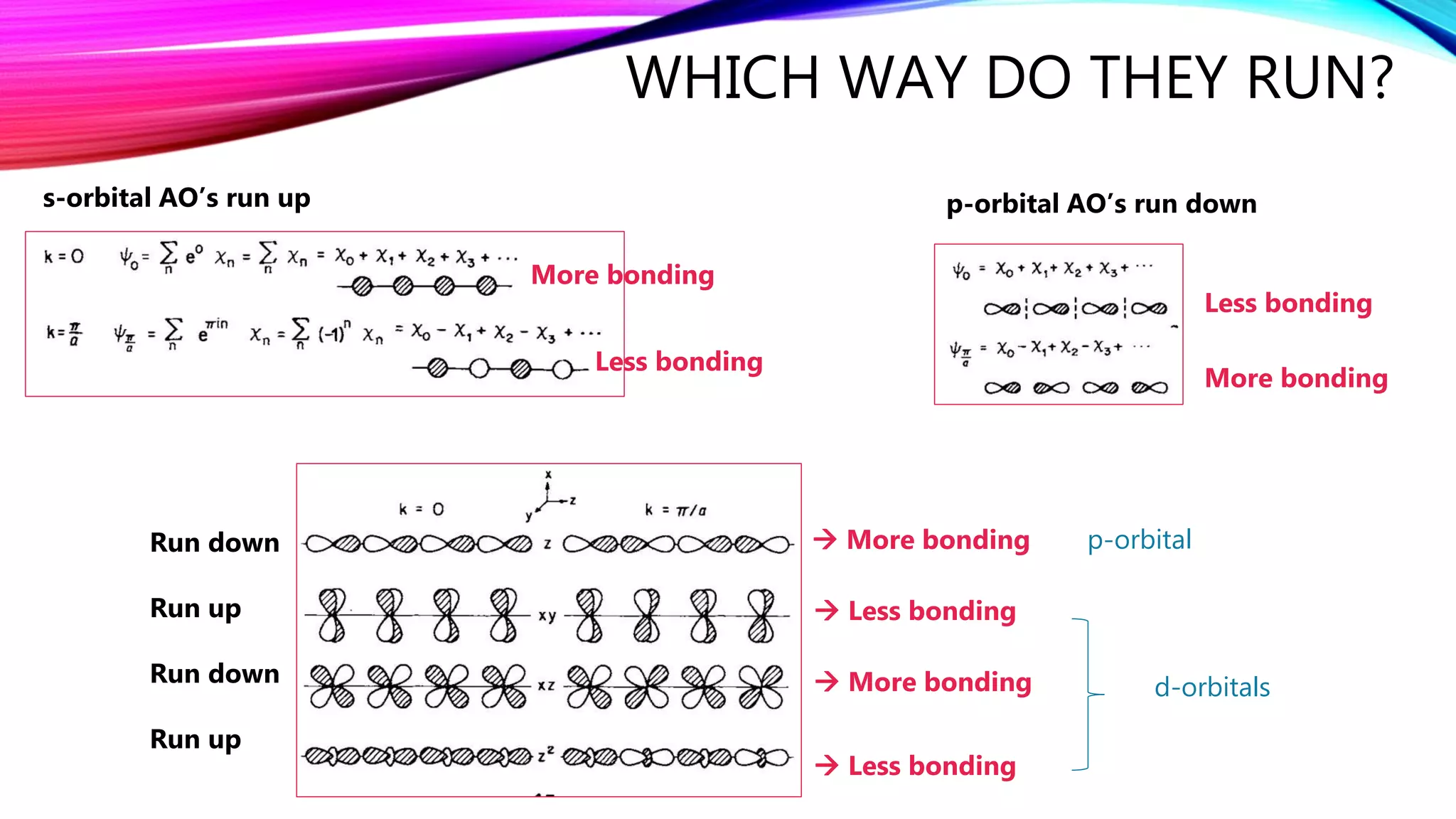
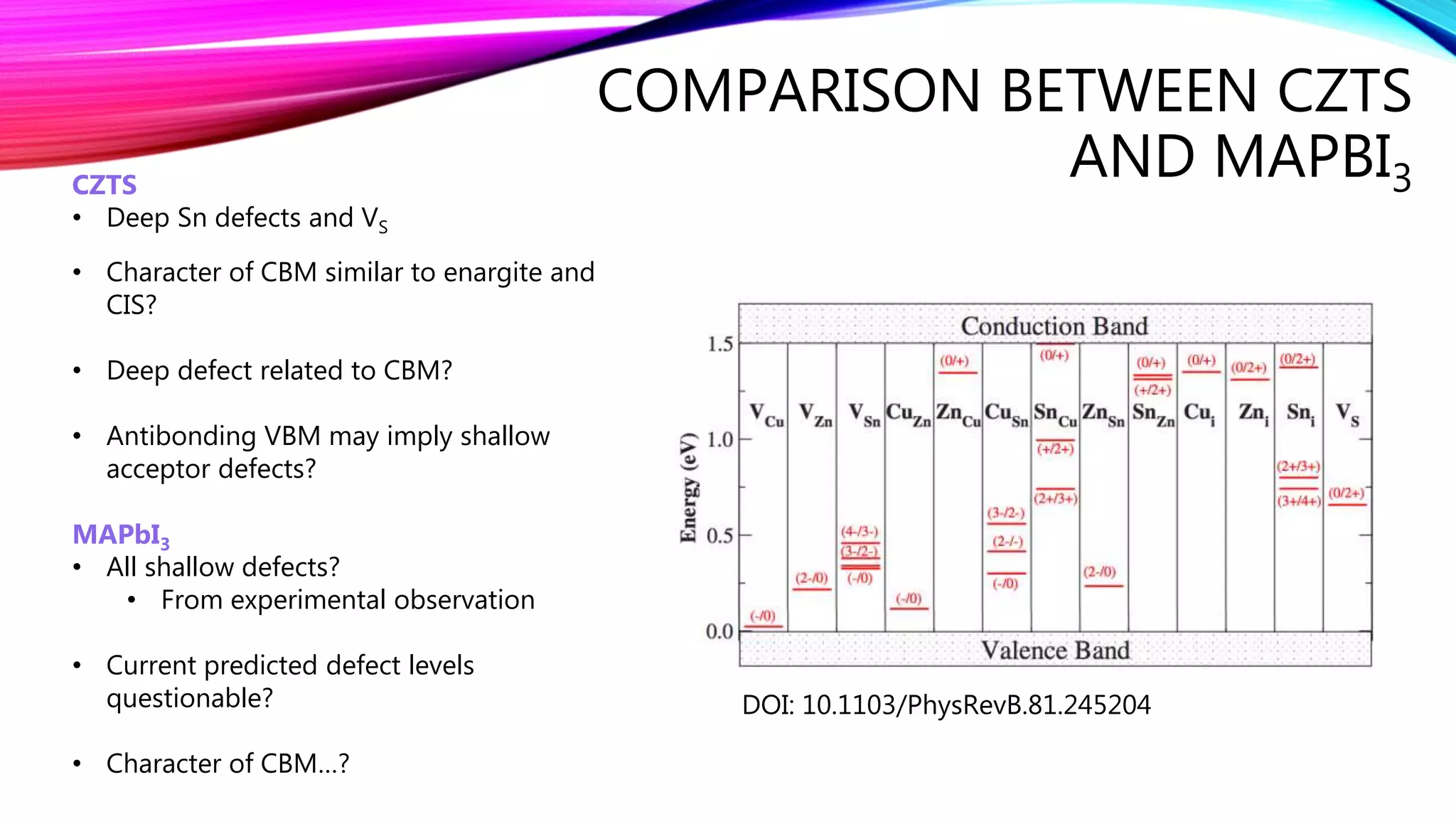
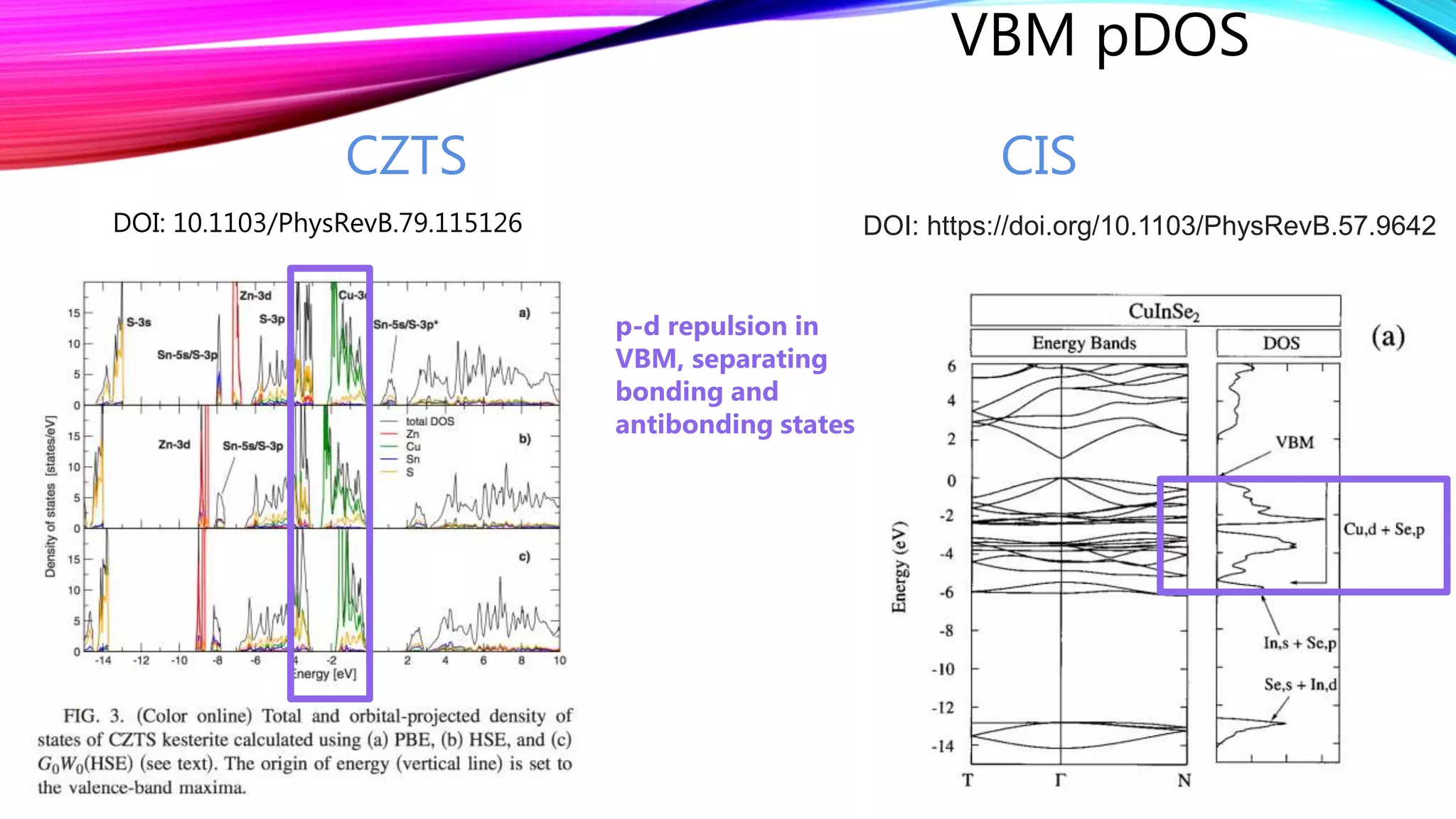
The document discusses predicting band structure without calculation by using Hoffmann's rules. It considers how factors like orbital overlap, dispersion, and structural distortions relate to bonding characteristics in band structures. For defects, it suggests deep levels could arise from many charge transition states, high orbital overlap at band extrema, or large lattice distortions. Extending the ideas to 1D, 2D, and 3D structures, it examines how orbital combinations at high symmetry points relate to bonding vs antibonding character. Structural distortions are noted to maximize bonding by altering densities of states.

Embed presentation

Download to read offline
WMD JOURNAL CLUB Suzanne Wallace 4th July 2017
Can we use Hoffmann’s knowledge for predicting band structures (without calculating them) … to predict defect-tolerance from ones that we have calculated? DOI: 10.1002/anie.198708461
Can we use Hoffmann’s knowledge for predicting band structures (without calculating them) … to predict defect-tolerance from ones that we have calculated? Probably not… but we all need a hobby, so I’ll have a go! DOI: 10.1002/anie.198708461
WHAT MAKES A DEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with a transition level deep in the band gap? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? 3. Large amount of distortion of the host lattice that the defect introduces?
WHAT MAKES A DEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with a transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? 3. Large amount of distortion of the host lattice that the defect introduces?
WHAT MAKES A DEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with a transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? See what Hoffmann says? 3. Large amount of distortion of the host lattice that the defect introduces? See what Hoffmann says?
DOI: 10.1002/anie.198708461 A veritable spaghetti diagram this, seemingly beyond the powers of comprehension of any human being. Why not abdicate understanding, just let the computer spew these bands out and accept (or distrust) them? No, that’s too easy a way out. We can understand much of this diagram. ‘ ’
DOI: 10.1002/anie.198708461 A veritable spaghetti diagram this, seemingly beyond the powers of comprehension of any human being. Why not abdicate understanding, just let the computer spew these bands out and accept (or distrust) them? No, that’s too easy a way out. We can understand much of this diagram. ‘ ‘With more, admittedly tedious, work, every aspect of these spaghetti diagrams can be understood.’ … ’
PROCEDURE FOR CONSTRUCTING BAND STRUCTURES (IN 1D)
ATOMIC ORBITALS AND BANDS IN 1D • Formation of bands from connecting AOs in 1D chains  (can extend to 3D) • Make use of translational symmetry to write Bloch functions: • Unique values of |k| are 0  𝜋/a • As many values of k as there are translations in crystal (microscopic unit cells in the macroscopic crystal)
PHYSICAL EXPLANATION: DISPERSION …suggests a highly dispersive band extrema AND minimal overlap not simultaneously possible? ‘One very important feature of a band is its dispersion, or band width, the difference in energy between the highest and lowest levels in the band’ ‘overlap between the interacting orbitals (in the polymer the overlap is that between neighboring unit cells).’ ‘The greater the overlap between neighbors, the greater the band width.' More overlap, more dispersion
PHYSICAL EXPLANATION: WHY BANDS RUN UP/ DOWN • s-orbitals: • p-orbitals: Seems sensible that you get (1x 𝜒n) for k=0 or (-1 x 𝜒n) for k= 𝜋/a … not so sure about intermediate values! Get fractional values? Is it even possible to NOT have an antibonding VBM? (if bands run from most bonding at lowest E to most antibonding at highest E) Does this depend on how far the band is filled up to?
ANTIBONDING BANDS? DOI: 10.1103/PhysRevB.79.115126 Band structure CBM MO diagram  A result of moving from combining AOs to combining MOs?  Dispersion is then related to bonding vs antibonding ways of combining bonding or antibonding MOs?
PREDICTING BAND STRUCTURE Based on: 1. Dispersion (how curvy) Difference in energy between k=0 and 𝜋 /a arrangement of AOs Extent of overlap (how much bonding character in most bonding state?) 2. Orbital topology (do they run up or down?) Does amount of bonding (and therefore energy) go up or down from k=0 to 𝜋/a? Both of above related to type of orbital!
WHICH WAY DO THEY RUN? s-orbital AO’s run up Run down Run up Run down Run up More bonding Less bonding More bonding Less bonding p-orbital AO’s run down  More bonding  More bonding  Less bonding  Less bonding d-orbitals p-orbital
HOW ABOUT HYBRIDISED ORBITALS? Does the topology of the orbital overlap just depend on what shape and parity of orbital you end up with after mixing?
HOW DISPERSE? Most disperse Most disperse Most physically close in bonding arrangement? • Related to extent of overlap • Difference in energy between most and least bonding arrangements of AOs (i.e. highest and lowest levels in the band)
HOW DISPERSE? • Related to extent of overlap • Difference in energy between most and least bonding arrangements of AOs (i.e. highest and lowest levels in the band) Least disperse Less disperse Least disperse band composed of least physically close AOs?
PROCEDURE FOR RECOVERING BONDS FROM DOS AND PDOS
CRYSTAL ORBITAL OVERLAP POPULATION (COOP) • For a two-centres orbital: • If c1 and c2 are the same sign overlap population ( ) is positive (bonding), negative (antibonding) if they are of opposite sign • Mulliken overlap population = summed over all orbitals on the two atoms over all occupied MOs • In a solid  Take all states within a certain energy interval, use to infer the bonding characteristics of the states
 Bonding or antibonding character at band extrema  At a glance, pDOS can tell us the effect of oxidation/ reduction on bond lengths CRYSTAL ORBITAL OVERLAP POPULATION (COOP)
EXTENSION TO MORE COMPLICATED SYSTEMS
> 1 UNIT CELL IN CHAIN • More complicated than 1D chain, e.g. • kinks in chain • reorientation of units/ staggered units • No. of bands = no. of MOs in unit cell • Band folding and redundancy • Multiplicity of bands due to enlargement of unit cell • Unfold to recover monomer • But with small perturbations, e.g. • More degeneracies for higher symmetry (e.g. rotated/ staggered units) ??  see next slide • Stabilisation/ destabilisation from bonding or antibonding next- nearest neighbour interactions in kinked chains
MORE DEGENERACY FOR STAGGERED UNITS? Extra degeneracy due to higher symmetry of staggered unit cell Seems slightly counter-intuitive for 2 unit cell system to have higher symmetry?
STRUCTURAL DISTORTIONS • Structures distort to maximise bonding/ pairing up of unpaired electrons in orbitals (free radicals) • Can be impeded by electron repulsions or steric effects preventing 2 radicals from being within bonding distance • In the solid state  equates to lowering the DOS at the Fermi level, moving bonding states to lower E and antibonding to high E • Orbitals of highly symmetrical structures (e.g. cubic or linear chains) often do not correspond to maximum bonding structures (hence so few SC structures?)
Jahn-Teller effect • Degenerate orbitals each with one electron • Structure distorts via vibrational mode to make one orbital lower in E so they pair up 2nd order Jahn-Teller effect • If orbital of species A is higher in E than species B, so cannot mix • Vibrational mode lowers symmetry to transform level A and B to equivalent E levels C to allow for bonding Peierls distortion (solid state equivalent of Jahn-Teller) • Degeneracy for any partially filled band • Deformation to lower E of system (more bonding) • Electron-phonon coupling • Degeneracies can be lifted by stabilising or destabilising • Effect is greatest for half-filled bands STRUCTURAL DISTORTIONS
A LITTLE MORE ON DISTORTION IN THE SOLID STATE • Structures distort to maximise bonding with a band is partially filled • Sounds sensible! • In the solid state, if the Fermi level of the undistorted structure would be expected to fall into a region with high DOS • Expect a structural distortion to occur • But why? Why should large DOS equate to unpaired e-? • A band gap can be created by the peierls distortion (moving some states to lower bonding states and others to higher antibonding states) • But does this imply that the Fermi level is in the gap? • Band gap always created in 1D • Band gap not always created in 3D systems • Can create a semiconductor or insulator • But also sometimes not possible for the structure to distort in such a way to remove all states from the Fermi level region so material is a conductor
EXTENSION TO 2D • Treat k (from earlier 1D chain) as a vector • Brillouin zone is now a 2D area • Simple 2D e.g.  H 1s orbital on 2D lattice Certain combinations between k=0, 𝜋/a or 𝜋/2a (𝛤 , M, X): Special points in B.Z.: Γ, X, M Hard to show all E(k) for all k, so show change in E along certain lines in B.Z. 𝜞 Lowest E M antibonding X nonbonding (as many bonding along y as antibonding along x)
P-ORBITALS IN 2D… Lattice perp to z-axis => pz orbital will be separated from px,y by symmetry  Orbitals cannot mix if not of the same nodal symmetry, to enable non-zero overlap? 𝜎, 𝜋 bonding and antibonding arrangements: s and p-orbitals of 2D H atom lattice along path: Use estimate that 𝜎 more important than 𝜋 bonding  Appearance of real band structure will depend on lattice spacing • Band dispersion increases with short contacts • Complications arise from s,p mixing?
EXTENSION TO 3D • Brillouin zone is now a 3D volume • 2D  3D: essentially, extra dimensions means extra bonds between layers, which means extra bands? • Hoffmann goes through some examples in detail • I’m just going to highlight what I found to be key points
3D: HIGHLIGHTS FROM EXAMPLES Example 1: V2S2 • No. of bands = no. of MOs in unit cell • 2 formula units in the hexagonal unit cell • Expect: 4 x 2 = 8 S bands (4: 1s and 3p-orbitals along period/ valence level) • Expect: 9 x 2 = 18 V bands (1s, 3p, 5d-orbitals along period/ valence level) • Count bands (note S 2s out of E range in figure) • 6 low-lying S 3p bands • 10 V 3d bands • Change in band structures of anion and metal sublattices when combined  • Crystal field splitting of V d orbitals
3D: HIGHLIGHTS FROM EXAMPLES Example 1: Mn2P2 2D layers – ordering of bands • The unit cell is a rhomboid of two Mn and two P atoms • P is clearly more electronegative than Mn  Expect two mainly P 3s bands below six P 3p bands below 10 Mn 3d bands Molecular picture: + Mn-Mn bonding in the solid
3D: HIGHLIGHTS FROM EXAMPLES Example 1: Mn2P2 2D layers – lone pairs! • P pz orbital  well localized, 70% in a band at ~15 eV • Localization in energy, implies localization in real space • The molecular orbitals of a crystal are always completely delocalized Bloch functions • Difference between • Symmetry enforced delocalization (formation of Bloch functions, little overlap) • Gives narrow bands • Real, chemical delocalization (overlap between unit cells) • Gives highly disperse bands • i.e. If you see narrow (flat) bands  sign of chemical localization • If you see dispersive (curvy) bands  implies real delocalization •  Implies lone pairs at frontier orbitals would give flat bands and poor carrier mobility? • 2D  3D: P 3pz orbitals or lone pairs in one layer form bonding or antibonding combinations with layers above or below
ATTEMPTING TO APPLY HOFFMANN’S WISDOM TO DEFECT-TOLERANCE CONSIDERATIONS…
1. PREDICTING DEFECT-TOLERANCE FROM FRONTIER ORBITALS/ BAND EXTREMA
WHAT MAKES A DEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? See what Hoffmann says? 3. Large amount of distortion of the host lattice that the defect introduces? See what Hoffmann says?
WHAT MAKES A DEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? See what Hoffmann says? 3. Large amount of distortion of the host lattice that the defect introduces? See what Hoffmann says?
2. OVERLAP AT BAND EXTREMA • Compute overlap population at band edges • …or can we just infer this from how dispersive the band edges are? (as discussed earlier) Implies a highly dispersive band edge and small overlap is not possible?
2. OVERLAP AT BAND EXTREMA • s,p orbitals are ‘diffuse’  large overlap  dispersive bands + mix with each other • d orbitals are ‘contracted’  flat bands • Sounds sensible that more spread out orbitals will mix more… s p d
2. OVERLAP AT BAND EXTREMA • s,p orbitals are ‘diffuse’  large overlap  dispersive bands + mix with each other • d orbitals are ‘contracted’  flat bands • Sounds sensible that more spread out orbitals will mix more… s p d
2. OVERLAP AT BAND EXTREMA  Implies s and p orbitals at band extrema will have a greater overlap  Could this mean that breaking bonds to form defects will be a larger perturbation on this type of band edge?  Implying more ’extreme’ dangling bonds?
2. OVERLAP AT BAND EXTREMA  Implies s and p orbitals at band extrema will have a greater overlap  Could this mean that breaking bonds to form defects will be a larger perturbation on this type of band edge?  Implying more ’extreme’ dangling bonds?
WHAT MAKES A DEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? See what Hoffmann says? 3. Large amount of distortion of the host lattice that the defect introduces? See what Hoffmann says?
3. HOST LATTICE DISTORTION & BONDING CHARACTER Oxidising/ removing electrons from antibonding states at VBM… Decreases separation of species involved in antibonding state Donor defects/ adding electrons to CBM… May increase or decrease separation of given species depending on if electrons go into bonding or antibonding states at CBM  Can lattice distortion act to compensate for that induced by the defect? … or above effects completely overshadowed by lattice distortion from point defect itself? …or is this only relevant to consider for shallow defects in the first place? (deep defects will be unlikely to add/ remove electrons to/ from continuum bands) (Can infer from COOP if CBM and VBM are bonding or antibonding)
2. TUNING THE FRONTIER ORBITALS FOR DEFECT-TOLERANCE?
WAYS TO TUNE ORBITALS PRESENT AT BAND EXTREMA? • pi-acceptors push pz down, pi-donors push it up • sigma-donors push dx2-y2 up • (pi-donor ligand = has filled non-bonding orbitals that overlap with metal- based orbitals) • Does this need to be done to very high-concentrations beyond doping? • Indication of ways to alloy for defect-tolerance possibly? • Or perhaps tuning cation to anion to give desirable frontier orbitals? • …Or possibly mixing up concepts here!
REDUCE BONDING AT THE BAND EXTREMA?A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? See what Hoffmann says? 3. Large amount of distortion of the host lattice that the defect introduces? See what Hoffmann says?
REDUCE BONDING AT THE BAND EXTREMA? • Can tune bond length (and hence strength) by choice of transition metal in Mn2P2 1. Weaker bonds (or nonbonding) at frontier orbitals may result in less deep defects when bonds are broken? 2. Distorting structure (through bond lengths) could possibly be used to compensate for defect-induced lattice distortion? • …of course we are limited by how free we are to tune materials for PV! • Still need good band gap/ absorption/ carrier mobility P-P in molecules usually 2.19  2.26 Å
REDUCE BONDING AT THE BAND EXTREMA? • In the middle of the transition series, the metal Fermi level is above the P-P 𝜎*. • Both 𝜎 and 𝜎 * are occupied • There is no resultant P-P bond • As P-P stretches in response, the 𝜎 * only becomes more filled • On the right side of the transition series, the P-P 𝜎* is above the Fermi level of the metal • So P-P 𝜎* is unfilled • The filled P-P 𝜎 makes a P-P bond • Making the P-P distance shorter only improves this situation • As transition metals moves to RHS of periodic table • Increased nuclear charge more incompletely screened • d electrons more tightly bound • d band comes down in energy and becomes narrower • Band filling increases
BONUS SLIDES AFTER GRATZEL’S TALK + SUNGHYUN’S RESULTS FOR VS
RE-VISITING HYPOTHESIS BASED ON BONDING CHARACTER OF BAND EXTREMA Vladan’s comment at EMRS – This is not compound (two molecules!) Michael Gratzel’s comment at CPE talk (in reference to MAPI): • Antibonding VBM and defect-tolerance • ‘you stabilise the system when breaking an antibonding bond’  Implies that only bonding character of filled states (i.e. the VBs) matter? (although this may not agree with high-throughput study by Vladan from EMRS, need to check)  May imply that which particular bonds are broken when particular defects form matter?  Possible to bias which types of defects form from processing conditions? DOI: 10.1021/jz5001787 DOI: 10.1021/acs.chemmater.6b05496
INVESTIGATING THEORY FOR CIS… VBM: • Cu d • Se p • some In s Shallow defects: • Vcu • Cui • Vse  compensating donor? Implies shallow? Deep defects (associated with breaking In bonds?): • VIn • CuIn Less deep: • InCu  involves breaking Cu bonds of host instead of In? Neutral aggregates in CIS (from Aron’s review): m(2VCu+In2+ Cu)0 units interlaced with n units of CuInSe2  Neutral aggregate doesn’t involve CuIn or VSe Contradictions for Vse (and others?) – see next …also VS in CZTS is deep? – or not given Sunghyun’s latest results! journals.aps.org/prb/pdf/10.1 103/PhysRevB.57.9642
INVESTIGATING THEORY FOR CIS… http://iopscience.iop.org/article/10.1088/0953-8984/23/42/422202/pdf Is it even possible for Vse to be an acceptor?!
CONCLUSIONS Hoffmann’s paper makes for a very interesting read! • Untangling the spaghetti of band structures! • But quite (conceptually) difficult to extrapolate to the more complicated systems we are interested in (for me at least)! …Implications for defect-tolerance? 1. Possible that extent of overlap (and hence s or p character) may be of some relevance?  Raises doubt over whether a disperse band edge with minimal overlap is possible! 2. Distortion of lattice due to defect-related redox possibly too minor an effect and only relevant for shallow defects anyway? 3. Choice of transition metal in compounds could tune strength of bonding at band extrema? – Although limited freedom due to other material requirements
CZTS DOI: 10.1103/PhysRevB.79.115126 Band structure MO diagram CBM
MAPBI3 PDOS & BAND STRUCTURE DOI: https://doi.org/10.1557/mrc.2015.26 doi:10.1038/srep04467
MO DIAGRAM…LINKED TO DEFECT- TOLERANCE? DOI: 10.1021/acs.chemmater.6b05496DOI: https://doi.org/10.1557/mrc.2015.26
COMPARISON BETWEEN CZTS AND MAPBI3 DOI: 10.1103/PhysRevB.81.245204 CZTS • Deep Sn defects and VS • Character of CBM similar to enargite and CIS? • Deep defect related to CBM? • Antibonding VBM may imply shallow acceptor defects? MAPbI3 • All shallow defects? • From experimental observation • Current predicted defect levels questionable? • Character of CBM…?
CZTS CIS DOI: 10.1103/PhysRevB.79.115126 DOI: https://doi.org/10.1103/PhysRevB.57.9642 p-d repulsion in VBM, separating bonding and antibonding states VBM pDOS
Enargite, Cu3AsS4 – similar VBM Stephanite, Ag5SbS4 (and bournonite, CuPbSbS3) - not similar (but still antibonding) p-d repulsion in VBM, separating bonding and antibonding states (enargite only) Similar As s-states and Cu p-states to CZTS Sn s-states and Cu p-states
THINKING MORE ABOUT CIS… • Defect-tolerant GBs (due to beneficial potential at GB, seems like pot luck!… see an old JC talk I did on this!) • Do get some deep-level defects... Just lucky that these have high formation energy or form benign defect complexes in ODC’s? DOI: https://doi.org/10.1103/PhysRevB.57.9642 • This electronic structure not necessarily related to shallow point defects? • ...just some lucky coincidences that reduce impact of deep defects?
CBM CHARACTER • Thoughts on MAPbI3’s defect-tolerance… • Problem is having a dataset of 1 super defect-tolerant material! • Possibly related to have p-states instead of s-states at CBM? • c.f. deep Sn and V_S defects in CZTS • Less overlap when s-orbitals not present? No sp hybridisation? • Possibly related to coordination? – octahedral coordination suppresses sp hybridisation?
P-CHARACTER OF CBM? DOI: https://doi.org/10.1557/mrc.2015.26
SP HYBRIDISATION AT CBM OF CZTS DOI: 10.1103/PhysRevB.79.115126 DOI: 10.1103/PhysRevB.81.245204

More Related Content

PPTX
Double slit
byhumakhan1357
 
PDF
Diffraction & Double Slit Experiment
bydwsutherland
 
PPTX
Chapter 5 diffraction
byGabriel O'Brien
 
PPT
Wave nature of_light
bybrihan123
 
PDF
SFB953.symposium
byStephan Hensel
 
PDF
Interference
byKrupesh Anadkat
 
PDF
Thin Film Interference Jennifer Whetter
byJennifer Whetter
 
PPTX
Microwave Devices Lecture10
byAmr Al-Awamry
 
Double slit
byhumakhan1357
 
Diffraction & Double Slit Experiment
bydwsutherland
 
Chapter 5 diffraction
byGabriel O'Brien
 
Wave nature of_light
bybrihan123
 
SFB953.symposium
byStephan Hensel
 
Interference
byKrupesh Anadkat
 
Thin Film Interference Jennifer Whetter
byJennifer Whetter
 
Microwave Devices Lecture10
byAmr Al-Awamry
 

Similar to Hoffmann band structures JC talk

PPTX
CH111_2025_AC_Lec9-10_Bonding-1 H2-mol-ion Diatomics updated.pptx
byneerajdevi7827560910
 
PDF
Inorganic materials 2019
byChris Sonntag
 
PDF
Inorganic materials Part 2/2
byChris Sonntag
 
PPTX
material selection for marin products 2.pptx
byeliya971130
 
PPT
Energy band theory of solids
byBarani Tharan
 
PDF
MSE_Structure of solids.pdf
byDIPS54
 
PPTX
Molecular orbital theory, 11(3)
byK. Shahzad Baig
 
PPTX
Bonding in metals
byLIFE SCIENCES
 
PPT
Ch02 m
byIbrahim Abuawwad
 
PPTX
Introduction to Crystal and their property.pptx
byrajnishsingh2000rr
 
PDF
Chapter-01.pdf 2235566789886758657776585
byshaneastronomo
 
PPT
Mot
byDrAdnanKhanAssistant
 
PPT
Molecular Orbital Theory basics
byV Bhuse
 
PPT
Chemical bonding part 2
byHoshi94
 
PPTX
Molecular orbital theory(mot) of SF6/CO2/I3-/B2H6
bysirakash
 
PDF
BONDING IN METALS BY K.N.S.SWAMI.pdf472.pdf
byAshutoshSingh319083
 
PPTX
Material science eeem
bySatyendra Mohan
 
PPTX
Material science eeem
bySatyendra Mohan
 
PDF
Bands-k-space.pdf
byJoaoVictor699728
 
PDF
Solid state chemistry.pdf
byMariaRayappanS
 
CH111_2025_AC_Lec9-10_Bonding-1 H2-mol-ion Diatomics updated.pptx
byneerajdevi7827560910
 
Inorganic materials 2019
byChris Sonntag
 
Inorganic materials Part 2/2
byChris Sonntag
 
material selection for marin products 2.pptx
byeliya971130
 
Energy band theory of solids
byBarani Tharan
 
MSE_Structure of solids.pdf
byDIPS54
 
Molecular orbital theory, 11(3)
byK. Shahzad Baig
 
Bonding in metals
byLIFE SCIENCES
 
Ch02 m
byIbrahim Abuawwad
 
Introduction to Crystal and their property.pptx
byrajnishsingh2000rr
 
Chapter-01.pdf 2235566789886758657776585
byshaneastronomo
 
Mot
byDrAdnanKhanAssistant
 
Molecular Orbital Theory basics
byV Bhuse
 
Chemical bonding part 2
byHoshi94
 
Molecular orbital theory(mot) of SF6/CO2/I3-/B2H6
bysirakash
 
BONDING IN METALS BY K.N.S.SWAMI.pdf472.pdf
byAshutoshSingh319083
 
Material science eeem
bySatyendra Mohan
 
Material science eeem
bySatyendra Mohan
 
Bands-k-space.pdf
byJoaoVictor699728
 
Solid state chemistry.pdf
byMariaRayappanS
 

More from Suzanne Wallace

PPTX
ML_in_QM_JC_02-10-18
bySuzanne Wallace
 
PPTX
defect_supercell_finite_size_schemes_10-09-18
bySuzanne Wallace
 
PPTX
DeepLearning_JC_talk
bySuzanne Wallace
 
PPTX
MRS Fall Meeting 2017
bySuzanne Wallace
 
PPTX
NREL PV seminar
bySuzanne Wallace
 
PPTX
NREL_rapid_development_intro
bySuzanne Wallace
 
PPTX
NREL_defect_tolerance
bySuzanne Wallace
 
PPTX
UG masters project
bySuzanne Wallace
 
PPTX
FE-PV JC talk
bySuzanne Wallace
 
PPTX
Defect tolerance
bySuzanne Wallace
 
PPTX
CZTS PL data JC talk
bySuzanne Wallace
 
PPTX
CIS GBs JC talk
bySuzanne Wallace
 
PPTX
Band alignment JC talk
bySuzanne Wallace
 
PPTX
APS March Meeting 2016
bySuzanne Wallace
 
PPTX
EMRS Meeting 2017
bySuzanne Wallace
 
ML_in_QM_JC_02-10-18
bySuzanne Wallace
 
defect_supercell_finite_size_schemes_10-09-18
bySuzanne Wallace
 
DeepLearning_JC_talk
bySuzanne Wallace
 
MRS Fall Meeting 2017
bySuzanne Wallace
 
NREL PV seminar
bySuzanne Wallace
 
NREL_rapid_development_intro
bySuzanne Wallace
 
NREL_defect_tolerance
bySuzanne Wallace
 
UG masters project
bySuzanne Wallace
 
FE-PV JC talk
bySuzanne Wallace
 
Defect tolerance
bySuzanne Wallace
 
CZTS PL data JC talk
bySuzanne Wallace
 
CIS GBs JC talk
bySuzanne Wallace
 
Band alignment JC talk
bySuzanne Wallace
 
APS March Meeting 2016
bySuzanne Wallace
 
EMRS Meeting 2017
bySuzanne Wallace
 

Recently uploaded

PDF
Radiation: graduate lecture slides on Cloud Physics UNR Course by Dr David Mi...
byDDM
 
PPT
Volcano and eruption ppt. for grade 8 students
byROLANARIBATO3
 
PDF
Cosmic-Ray Bath in a Past Supernova Gives Birth to Earth-Like Planets
bySérgio Sacani
 
PDF
Campbell Biology 12th Edition PDF Textbook
bywosarix923
 
PDF
CosmologywithVoidsfromtheNancyGraceRomanSpaceTelescope
bySérgio Sacani
 
PPT
LIPIDS, LIPOPROTEINS AND DISORDERS-2.ppt
byikofrank15
 
PDF
AThickVolatileAtmosphereontheUltrahotSuper-EarthTOI-561b
bySérgio Sacani
 
PDF
Class - 10 Science Book Full Concept Explanation With Last Five Years Solved ...
byDr. Juber Hawaldar
 
PPTX
Advances in Monoclonal Antibody.pptxaaaaa
bya7medelmnifi
 
PPTX
Inborn errors of metabolism carbs & Protein
byharikasnvmv
 
PDF
MultispacecraftMeasurementsof theEvolvingGeometryof theSolarAlfvénSurface ove...
bySérgio Sacani
 
PPTX
RESTRICTION ENDONUCLEASE ,TYPES , MECHANISM , APPLICATION
byRemya M S
 
PDF
Enhancing the Role of Knowledge Holders in the UN CBD: Pioneering Capacity-Bu...
bypensoftservices
 
PPTX
LEAD IDENTIFICATION for pharmacognosy.pptx
byTejaswini Chandra
 
PPTX
Determination of Permanent Wilting Point (PWP) by Sunflower pot culture techn...
bySaurabh Upadhyay
 
PDF
Complications of Blood Transfusion.pdf Karrar Hayder K. Rustum
bykarrarhayderm
 
PPTX
Epigenetics (Protein translation, Genetic Code, Steps involved in Translation...
byRashmiMG2
 
PDF
Biopsychology 10th Edition PDF by John P. J. Pinel
bykonivon907
 
PDF
Introduction of bioinformatics in hindi ( जैव सूचना विज्ञान का परिचय ) @irfan...
byWorld of Wisdom
 
PDF
ZTF25abjmnps (AT2025ulz) and S250818k: A Candidate Superkilonova from a Subth...
bySérgio Sacani
 
Radiation: graduate lecture slides on Cloud Physics UNR Course by Dr David Mi...
byDDM
 
Volcano and eruption ppt. for grade 8 students
byROLANARIBATO3
 
Cosmic-Ray Bath in a Past Supernova Gives Birth to Earth-Like Planets
bySérgio Sacani
 
Campbell Biology 12th Edition PDF Textbook
bywosarix923
 
CosmologywithVoidsfromtheNancyGraceRomanSpaceTelescope
bySérgio Sacani
 
LIPIDS, LIPOPROTEINS AND DISORDERS-2.ppt
byikofrank15
 
AThickVolatileAtmosphereontheUltrahotSuper-EarthTOI-561b
bySérgio Sacani
 
Class - 10 Science Book Full Concept Explanation With Last Five Years Solved ...
byDr. Juber Hawaldar
 
Advances in Monoclonal Antibody.pptxaaaaa
bya7medelmnifi
 
Inborn errors of metabolism carbs & Protein
byharikasnvmv
 
MultispacecraftMeasurementsof theEvolvingGeometryof theSolarAlfvénSurface ove...
bySérgio Sacani
 
RESTRICTION ENDONUCLEASE ,TYPES , MECHANISM , APPLICATION
byRemya M S
 
Enhancing the Role of Knowledge Holders in the UN CBD: Pioneering Capacity-Bu...
bypensoftservices
 
LEAD IDENTIFICATION for pharmacognosy.pptx
byTejaswini Chandra
 
Determination of Permanent Wilting Point (PWP) by Sunflower pot culture techn...
bySaurabh Upadhyay
 
Complications of Blood Transfusion.pdf Karrar Hayder K. Rustum
bykarrarhayderm
 
Epigenetics (Protein translation, Genetic Code, Steps involved in Translation...
byRashmiMG2
 
Biopsychology 10th Edition PDF by John P. J. Pinel
bykonivon907
 
Introduction of bioinformatics in hindi ( जैव सूचना विज्ञान का परिचय ) @irfan...
byWorld of Wisdom
 
ZTF25abjmnps (AT2025ulz) and S250818k: A Candidate Superkilonova from a Subth...
bySérgio Sacani
 

Hoffmann band structures JC talk

  • 1.
    WMD JOURNAL CLUB SuzanneWallace 4th July 2017
  • 2.
    Can we useHoffmann’s knowledge for predicting band structures (without calculating them) … to predict defect-tolerance from ones that we have calculated? DOI: 10.1002/anie.198708461
  • 3.
    Can we useHoffmann’s knowledge for predicting band structures (without calculating them) … to predict defect-tolerance from ones that we have calculated? Probably not… but we all need a hobby, so I’ll have a go! DOI: 10.1002/anie.198708461
  • 4.
    WHAT MAKES ADEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with a transition level deep in the band gap? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? 3. Large amount of distortion of the host lattice that the defect introduces?
  • 5.
    WHAT MAKES ADEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with a transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? 3. Large amount of distortion of the host lattice that the defect introduces?
  • 6.
    WHAT MAKES ADEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with a transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? See what Hoffmann says? 3. Large amount of distortion of the host lattice that the defect introduces? See what Hoffmann says?
  • 7.
    DOI: 10.1002/anie.198708461 A veritablespaghetti diagram this, seemingly beyond the powers of comprehension of any human being. Why not abdicate understanding, just let the computer spew these bands out and accept (or distrust) them? No, that’s too easy a way out. We can understand much of this diagram. ‘ ’
  • 8.
    DOI: 10.1002/anie.198708461 A veritablespaghetti diagram this, seemingly beyond the powers of comprehension of any human being. Why not abdicate understanding, just let the computer spew these bands out and accept (or distrust) them? No, that’s too easy a way out. We can understand much of this diagram. ‘ ‘With more, admittedly tedious, work, every aspect of these spaghetti diagrams can be understood.’ … ’
  • 9.
    PROCEDURE FOR CONSTRUCTINGBAND STRUCTURES (IN 1D)
  • 10.
    ATOMIC ORBITALS ANDBANDS IN 1D • Formation of bands from connecting AOs in 1D chains  (can extend to 3D) • Make use of translational symmetry to write Bloch functions: • Unique values of |k| are 0  𝜋/a • As many values of k as there are translations in crystal (microscopic unit cells in the macroscopic crystal)
  • 11.
    PHYSICAL EXPLANATION: DISPERSION …suggestsa highly dispersive band extrema AND minimal overlap not simultaneously possible? ‘One very important feature of a band is its dispersion, or band width, the difference in energy between the highest and lowest levels in the band’ ‘overlap between the interacting orbitals (in the polymer the overlap is that between neighboring unit cells).’ ‘The greater the overlap between neighbors, the greater the band width.' More overlap, more dispersion
  • 12.
    PHYSICAL EXPLANATION: WHY BANDSRUN UP/ DOWN • s-orbitals: • p-orbitals: Seems sensible that you get (1x 𝜒n) for k=0 or (-1 x 𝜒n) for k= 𝜋/a … not so sure about intermediate values! Get fractional values? Is it even possible to NOT have an antibonding VBM? (if bands run from most bonding at lowest E to most antibonding at highest E) Does this depend on how far the band is filled up to?
  • 13.
    ANTIBONDING BANDS? DOI: 10.1103/PhysRevB.79.115126 Bandstructure CBM MO diagram  A result of moving from combining AOs to combining MOs?  Dispersion is then related to bonding vs antibonding ways of combining bonding or antibonding MOs?
  • 14.
    PREDICTING BAND STRUCTURE Basedon: 1. Dispersion (how curvy) Difference in energy between k=0 and 𝜋 /a arrangement of AOs Extent of overlap (how much bonding character in most bonding state?) 2. Orbital topology (do they run up or down?) Does amount of bonding (and therefore energy) go up or down from k=0 to 𝜋/a? Both of above related to type of orbital!
  • 15.
    WHICH WAY DOTHEY RUN? s-orbital AO’s run up Run down Run up Run down Run up More bonding Less bonding More bonding Less bonding p-orbital AO’s run down  More bonding  More bonding  Less bonding  Less bonding d-orbitals p-orbital
  • 16.
    HOW ABOUT HYBRIDISEDORBITALS? Does the topology of the orbital overlap just depend on what shape and parity of orbital you end up with after mixing?
  • 17.
    HOW DISPERSE? Most disperse Mostdisperse Most physically close in bonding arrangement? • Related to extent of overlap • Difference in energy between most and least bonding arrangements of AOs (i.e. highest and lowest levels in the band)
  • 18.
    HOW DISPERSE? • Relatedto extent of overlap • Difference in energy between most and least bonding arrangements of AOs (i.e. highest and lowest levels in the band) Least disperse Less disperse Least disperse band composed of least physically close AOs?
  • 19.
  • 20.
    CRYSTAL ORBITAL OVERLAP POPULATION(COOP) • For a two-centres orbital: • If c1 and c2 are the same sign overlap population ( ) is positive (bonding), negative (antibonding) if they are of opposite sign • Mulliken overlap population = summed over all orbitals on the two atoms over all occupied MOs • In a solid  Take all states within a certain energy interval, use to infer the bonding characteristics of the states
  • 21.
     Bonding orantibonding character at band extrema  At a glance, pDOS can tell us the effect of oxidation/ reduction on bond lengths CRYSTAL ORBITAL OVERLAP POPULATION (COOP)
  • 22.
    EXTENSION TO MORECOMPLICATED SYSTEMS
  • 23.
    > 1 UNITCELL IN CHAIN • More complicated than 1D chain, e.g. • kinks in chain • reorientation of units/ staggered units • No. of bands = no. of MOs in unit cell • Band folding and redundancy • Multiplicity of bands due to enlargement of unit cell • Unfold to recover monomer • But with small perturbations, e.g. • More degeneracies for higher symmetry (e.g. rotated/ staggered units) ??  see next slide • Stabilisation/ destabilisation from bonding or antibonding next- nearest neighbour interactions in kinked chains
  • 24.
    MORE DEGENERACY FOR STAGGEREDUNITS? Extra degeneracy due to higher symmetry of staggered unit cell Seems slightly counter-intuitive for 2 unit cell system to have higher symmetry?
  • 25.
    STRUCTURAL DISTORTIONS • Structuresdistort to maximise bonding/ pairing up of unpaired electrons in orbitals (free radicals) • Can be impeded by electron repulsions or steric effects preventing 2 radicals from being within bonding distance • In the solid state  equates to lowering the DOS at the Fermi level, moving bonding states to lower E and antibonding to high E • Orbitals of highly symmetrical structures (e.g. cubic or linear chains) often do not correspond to maximum bonding structures (hence so few SC structures?)
  • 26.
    Jahn-Teller effect • Degenerateorbitals each with one electron • Structure distorts via vibrational mode to make one orbital lower in E so they pair up 2nd order Jahn-Teller effect • If orbital of species A is higher in E than species B, so cannot mix • Vibrational mode lowers symmetry to transform level A and B to equivalent E levels C to allow for bonding Peierls distortion (solid state equivalent of Jahn-Teller) • Degeneracy for any partially filled band • Deformation to lower E of system (more bonding) • Electron-phonon coupling • Degeneracies can be lifted by stabilising or destabilising • Effect is greatest for half-filled bands STRUCTURAL DISTORTIONS
  • 27.
    A LITTLE MOREON DISTORTION IN THE SOLID STATE • Structures distort to maximise bonding with a band is partially filled • Sounds sensible! • In the solid state, if the Fermi level of the undistorted structure would be expected to fall into a region with high DOS • Expect a structural distortion to occur • But why? Why should large DOS equate to unpaired e-? • A band gap can be created by the peierls distortion (moving some states to lower bonding states and others to higher antibonding states) • But does this imply that the Fermi level is in the gap? • Band gap always created in 1D • Band gap not always created in 3D systems • Can create a semiconductor or insulator • But also sometimes not possible for the structure to distort in such a way to remove all states from the Fermi level region so material is a conductor
  • 28.
    EXTENSION TO 2D •Treat k (from earlier 1D chain) as a vector • Brillouin zone is now a 2D area • Simple 2D e.g.  H 1s orbital on 2D lattice Certain combinations between k=0, 𝜋/a or 𝜋/2a (𝛤 , M, X): Special points in B.Z.: Γ, X, M Hard to show all E(k) for all k, so show change in E along certain lines in B.Z. 𝜞 Lowest E M antibonding X nonbonding (as many bonding along y as antibonding along x)
  • 29.
    P-ORBITALS IN 2D… Latticeperp to z-axis => pz orbital will be separated from px,y by symmetry  Orbitals cannot mix if not of the same nodal symmetry, to enable non-zero overlap? 𝜎, 𝜋 bonding and antibonding arrangements: s and p-orbitals of 2D H atom lattice along path: Use estimate that 𝜎 more important than 𝜋 bonding  Appearance of real band structure will depend on lattice spacing • Band dispersion increases with short contacts • Complications arise from s,p mixing?
  • 30.
    EXTENSION TO 3D •Brillouin zone is now a 3D volume • 2D  3D: essentially, extra dimensions means extra bonds between layers, which means extra bands? • Hoffmann goes through some examples in detail • I’m just going to highlight what I found to be key points
  • 31.
    3D: HIGHLIGHTS FROMEXAMPLES Example 1: V2S2 • No. of bands = no. of MOs in unit cell • 2 formula units in the hexagonal unit cell • Expect: 4 x 2 = 8 S bands (4: 1s and 3p-orbitals along period/ valence level) • Expect: 9 x 2 = 18 V bands (1s, 3p, 5d-orbitals along period/ valence level) • Count bands (note S 2s out of E range in figure) • 6 low-lying S 3p bands • 10 V 3d bands • Change in band structures of anion and metal sublattices when combined  • Crystal field splitting of V d orbitals
  • 32.
    3D: HIGHLIGHTS FROMEXAMPLES Example 1: Mn2P2 2D layers – ordering of bands • The unit cell is a rhomboid of two Mn and two P atoms • P is clearly more electronegative than Mn  Expect two mainly P 3s bands below six P 3p bands below 10 Mn 3d bands Molecular picture: + Mn-Mn bonding in the solid
  • 33.
    3D: HIGHLIGHTS FROMEXAMPLES Example 1: Mn2P2 2D layers – lone pairs! • P pz orbital  well localized, 70% in a band at ~15 eV • Localization in energy, implies localization in real space • The molecular orbitals of a crystal are always completely delocalized Bloch functions • Difference between • Symmetry enforced delocalization (formation of Bloch functions, little overlap) • Gives narrow bands • Real, chemical delocalization (overlap between unit cells) • Gives highly disperse bands • i.e. If you see narrow (flat) bands  sign of chemical localization • If you see dispersive (curvy) bands  implies real delocalization •  Implies lone pairs at frontier orbitals would give flat bands and poor carrier mobility? • 2D  3D: P 3pz orbitals or lone pairs in one layer form bonding or antibonding combinations with layers above or below
  • 34.
    ATTEMPTING TO APPLYHOFFMANN’S WISDOM TO DEFECT-TOLERANCE CONSIDERATIONS…
  • 35.
    1. PREDICTING DEFECT-TOLERANCEFROM FRONTIER ORBITALS/ BAND EXTREMA
  • 36.
    WHAT MAKES ADEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? See what Hoffmann says? 3. Large amount of distortion of the host lattice that the defect introduces? See what Hoffmann says?
  • 37.
    WHAT MAKES ADEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? See what Hoffmann says? 3. Large amount of distortion of the host lattice that the defect introduces? See what Hoffmann says?
  • 38.
    2. OVERLAP ATBAND EXTREMA • Compute overlap population at band edges • …or can we just infer this from how dispersive the band edges are? (as discussed earlier) Implies a highly dispersive band edge and small overlap is not possible?
  • 39.
    2. OVERLAP ATBAND EXTREMA • s,p orbitals are ‘diffuse’  large overlap  dispersive bands + mix with each other • d orbitals are ‘contracted’  flat bands • Sounds sensible that more spread out orbitals will mix more… s p d
  • 40.
    2. OVERLAP ATBAND EXTREMA • s,p orbitals are ‘diffuse’  large overlap  dispersive bands + mix with each other • d orbitals are ‘contracted’  flat bands • Sounds sensible that more spread out orbitals will mix more… s p d
  • 41.
    2. OVERLAP ATBAND EXTREMA  Implies s and p orbitals at band extrema will have a greater overlap  Could this mean that breaking bonds to form defects will be a larger perturbation on this type of band edge?  Implying more ’extreme’ dangling bonds?
  • 42.
    2. OVERLAP ATBAND EXTREMA  Implies s and p orbitals at band extrema will have a greater overlap  Could this mean that breaking bonds to form defects will be a larger perturbation on this type of band edge?  Implying more ’extreme’ dangling bonds?
  • 43.
    WHAT MAKES ADEFECT DEEP? A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? See what Hoffmann says? 3. Large amount of distortion of the host lattice that the defect introduces? See what Hoffmann says?
  • 44.
    3. HOST LATTICEDISTORTION & BONDING CHARACTER Oxidising/ removing electrons from antibonding states at VBM… Decreases separation of species involved in antibonding state Donor defects/ adding electrons to CBM… May increase or decrease separation of given species depending on if electrons go into bonding or antibonding states at CBM  Can lattice distortion act to compensate for that induced by the defect? … or above effects completely overshadowed by lattice distortion from point defect itself? …or is this only relevant to consider for shallow defects in the first place? (deep defects will be unlikely to add/ remove electrons to/ from continuum bands) (Can infer from COOP if CBM and VBM are bonding or antibonding)
  • 45.
    2. TUNING THEFRONTIER ORBITALS FOR DEFECT-TOLERANCE?
  • 46.
    WAYS TO TUNEORBITALS PRESENT AT BAND EXTREMA? • pi-acceptors push pz down, pi-donors push it up • sigma-donors push dx2-y2 up • (pi-donor ligand = has filled non-bonding orbitals that overlap with metal- based orbitals) • Does this need to be done to very high-concentrations beyond doping? • Indication of ways to alloy for defect-tolerance possibly? • Or perhaps tuning cation to anion to give desirable frontier orbitals? • …Or possibly mixing up concepts here!
  • 47.
    REDUCE BONDING ATTHE BAND EXTREMA?A couple of ideas… 1. A defect with several different charge transition states is more likely to result in one with transition level deep in the band gap? Infer from redox energy and/ or Marcus theory? 2. Large amount of overlap between states at the band extrema for the bonds that will be broken when defects are formed? See what Hoffmann says? 3. Large amount of distortion of the host lattice that the defect introduces? See what Hoffmann says?
  • 48.
    REDUCE BONDING ATTHE BAND EXTREMA? • Can tune bond length (and hence strength) by choice of transition metal in Mn2P2 1. Weaker bonds (or nonbonding) at frontier orbitals may result in less deep defects when bonds are broken? 2. Distorting structure (through bond lengths) could possibly be used to compensate for defect-induced lattice distortion? • …of course we are limited by how free we are to tune materials for PV! • Still need good band gap/ absorption/ carrier mobility P-P in molecules usually 2.19  2.26 Å
  • 49.
    REDUCE BONDING ATTHE BAND EXTREMA? • In the middle of the transition series, the metal Fermi level is above the P-P 𝜎*. • Both 𝜎 and 𝜎 * are occupied • There is no resultant P-P bond • As P-P stretches in response, the 𝜎 * only becomes more filled • On the right side of the transition series, the P-P 𝜎* is above the Fermi level of the metal • So P-P 𝜎* is unfilled • The filled P-P 𝜎 makes a P-P bond • Making the P-P distance shorter only improves this situation • As transition metals moves to RHS of periodic table • Increased nuclear charge more incompletely screened • d electrons more tightly bound • d band comes down in energy and becomes narrower • Band filling increases
  • 50.
    BONUS SLIDES AFTERGRATZEL’S TALK + SUNGHYUN’S RESULTS FOR VS
  • 51.
    RE-VISITING HYPOTHESIS BASEDON BONDING CHARACTER OF BAND EXTREMA Vladan’s comment at EMRS – This is not compound (two molecules!) Michael Gratzel’s comment at CPE talk (in reference to MAPI): • Antibonding VBM and defect-tolerance • ‘you stabilise the system when breaking an antibonding bond’  Implies that only bonding character of filled states (i.e. the VBs) matter? (although this may not agree with high-throughput study by Vladan from EMRS, need to check)  May imply that which particular bonds are broken when particular defects form matter?  Possible to bias which types of defects form from processing conditions? DOI: 10.1021/jz5001787 DOI: 10.1021/acs.chemmater.6b05496
  • 52.
    INVESTIGATING THEORY FORCIS… VBM: • Cu d • Se p • some In s Shallow defects: • Vcu • Cui • Vse  compensating donor? Implies shallow? Deep defects (associated with breaking In bonds?): • VIn • CuIn Less deep: • InCu  involves breaking Cu bonds of host instead of In? Neutral aggregates in CIS (from Aron’s review): m(2VCu+In2+ Cu)0 units interlaced with n units of CuInSe2  Neutral aggregate doesn’t involve CuIn or VSe Contradictions for Vse (and others?) – see next …also VS in CZTS is deep? – or not given Sunghyun’s latest results! journals.aps.org/prb/pdf/10.1 103/PhysRevB.57.9642
  • 53.
    INVESTIGATING THEORY FORCIS… http://iopscience.iop.org/article/10.1088/0953-8984/23/42/422202/pdf Is it even possible for Vse to be an acceptor?!
  • 54.
    CONCLUSIONS Hoffmann’s paper makesfor a very interesting read! • Untangling the spaghetti of band structures! • But quite (conceptually) difficult to extrapolate to the more complicated systems we are interested in (for me at least)! …Implications for defect-tolerance? 1. Possible that extent of overlap (and hence s or p character) may be of some relevance?  Raises doubt over whether a disperse band edge with minimal overlap is possible! 2. Distortion of lattice due to defect-related redox possibly too minor an effect and only relevant for shallow defects anyway? 3. Choice of transition metal in compounds could tune strength of bonding at band extrema? – Although limited freedom due to other material requirements
  • 55.
  • 56.
    MAPBI3 PDOS &BAND STRUCTURE DOI: https://doi.org/10.1557/mrc.2015.26 doi:10.1038/srep04467
  • 57.
    MO DIAGRAM…LINKED TODEFECT- TOLERANCE? DOI: 10.1021/acs.chemmater.6b05496DOI: https://doi.org/10.1557/mrc.2015.26
  • 58.
    COMPARISON BETWEEN CZTS ANDMAPBI3 DOI: 10.1103/PhysRevB.81.245204 CZTS • Deep Sn defects and VS • Character of CBM similar to enargite and CIS? • Deep defect related to CBM? • Antibonding VBM may imply shallow acceptor defects? MAPbI3 • All shallow defects? • From experimental observation • Current predicted defect levels questionable? • Character of CBM…?
  • 59.
    CZTS CIS DOI: 10.1103/PhysRevB.79.115126DOI: https://doi.org/10.1103/PhysRevB.57.9642 p-d repulsion in VBM, separating bonding and antibonding states VBM pDOS
  • 60.
    Enargite, Cu3AsS4 –similar VBM Stephanite, Ag5SbS4 (and bournonite, CuPbSbS3) - not similar (but still antibonding) p-d repulsion in VBM, separating bonding and antibonding states (enargite only) Similar As s-states and Cu p-states to CZTS Sn s-states and Cu p-states
  • 61.
    THINKING MORE ABOUTCIS… • Defect-tolerant GBs (due to beneficial potential at GB, seems like pot luck!… see an old JC talk I did on this!) • Do get some deep-level defects... Just lucky that these have high formation energy or form benign defect complexes in ODC’s? DOI: https://doi.org/10.1103/PhysRevB.57.9642 • This electronic structure not necessarily related to shallow point defects? • ...just some lucky coincidences that reduce impact of deep defects?
  • 62.
    CBM CHARACTER • Thoughtson MAPbI3’s defect-tolerance… • Problem is having a dataset of 1 super defect-tolerant material! • Possibly related to have p-states instead of s-states at CBM? • c.f. deep Sn and V_S defects in CZTS • Less overlap when s-orbitals not present? No sp hybridisation? • Possibly related to coordination? – octahedral coordination suppresses sp hybridisation?
  • 63.
    P-CHARACTER OF CBM? DOI:https://doi.org/10.1557/mrc.2015.26
  • 64.
    SP HYBRIDISATION ATCBM OF CZTS DOI: 10.1103/PhysRevB.79.115126 DOI: 10.1103/PhysRevB.81.245204