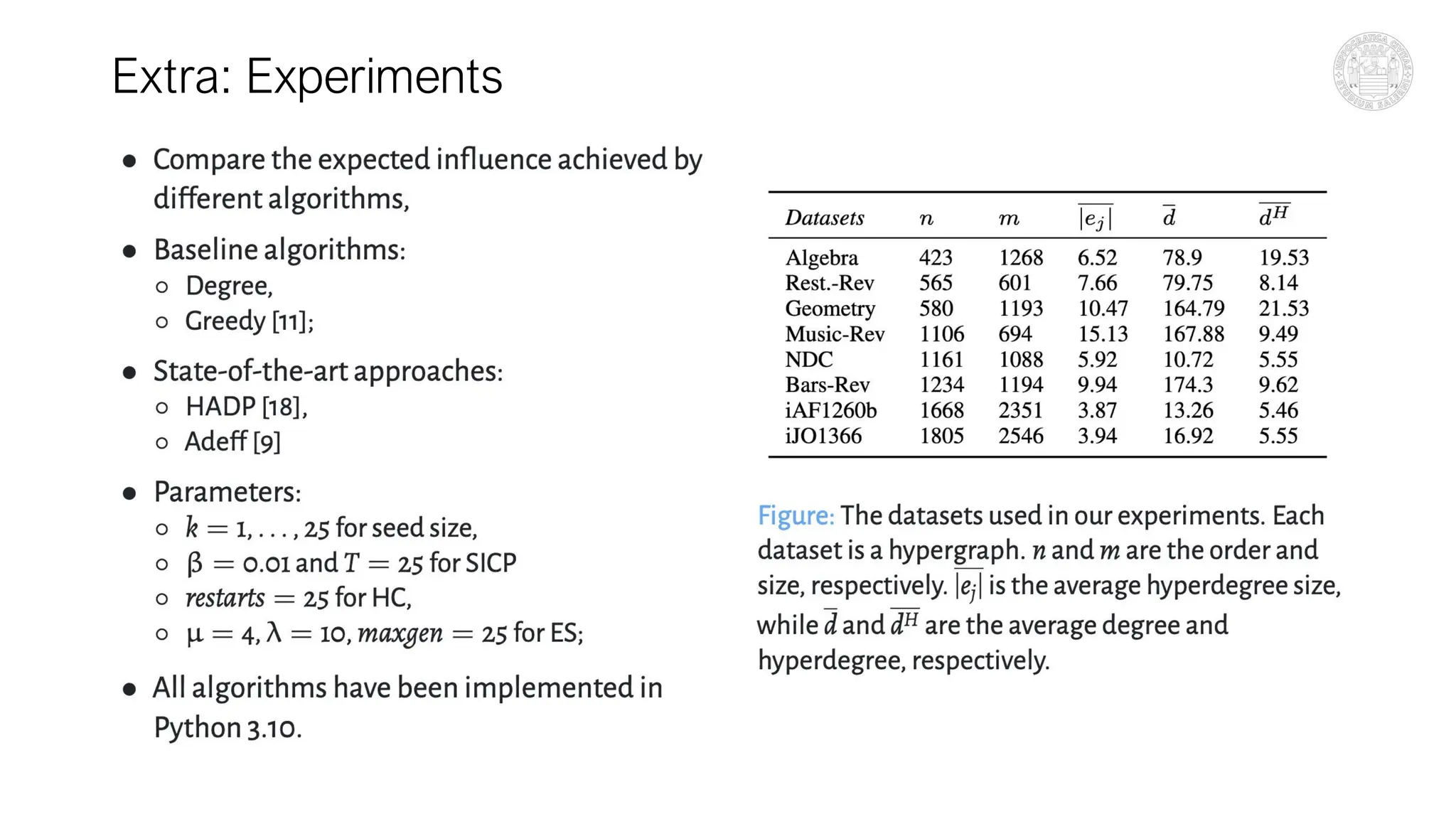
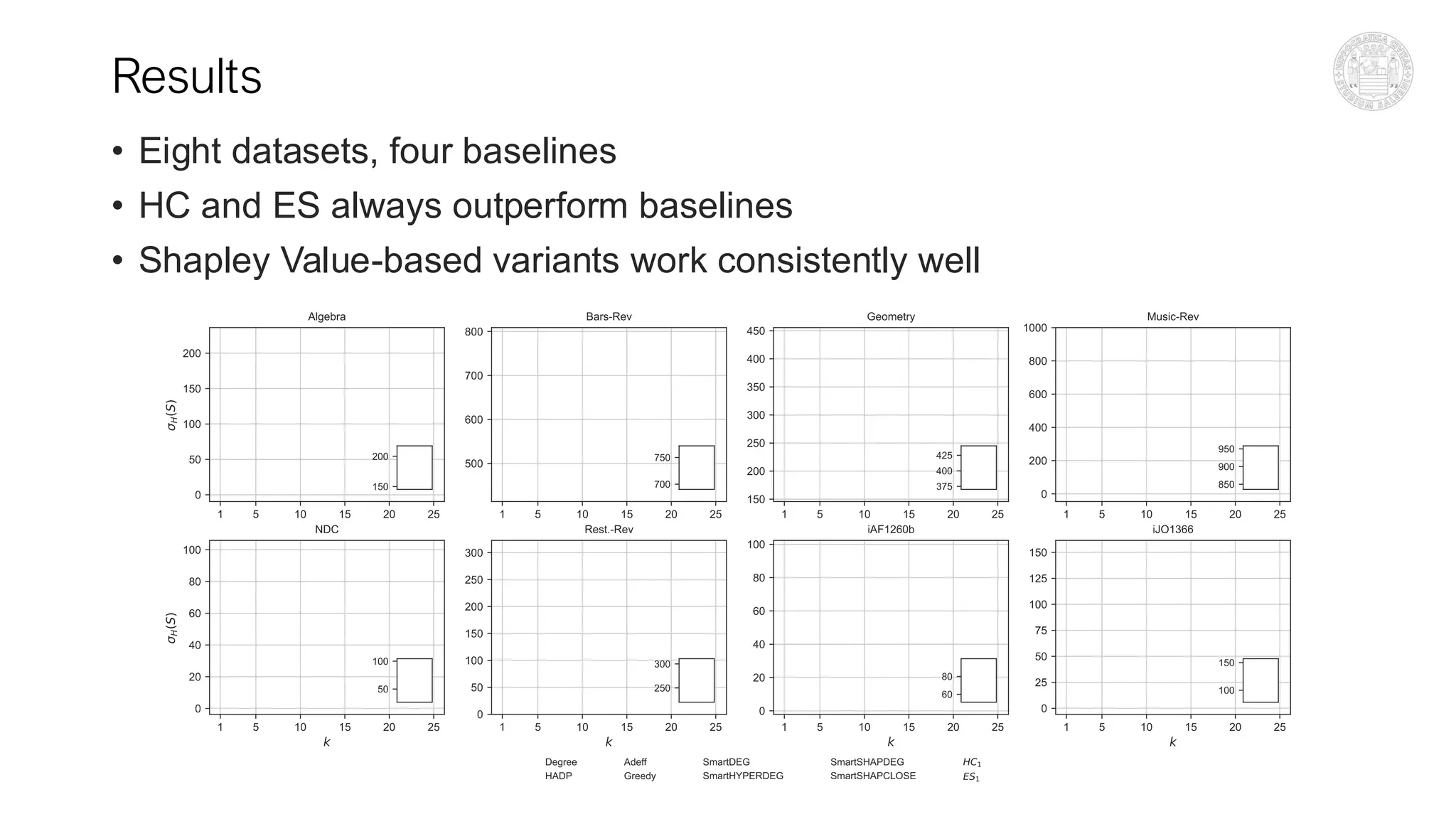
The document discusses algorithms for influence maximization (IM) in hypergraphs, which model higher-order interactions important for fields like marketing and social systems. Three main algorithms are proposed: SmartProps, HC (hill climbing), and ES (evolutionary strategies), with variations that utilize node properties and game-theoretic measures for improved performance. The proposed methods consistently outperform baseline approaches in simulations conducted on eight datasets, highlighting the significance of game-theoretic centrality in IM problems on hypergraphs.

1. Heuristics Approaches for the Influence Maximization
Problem on Hypergraphs
Vincenzo Auletta, Francesco Cauteruccio and Diodato Ferraioli
Department of Information Engineering, Electrical Engineering and Applied Mathematics (DIEM)
University of Salerno, Italy
{auletta,fcauteruccio,dferraioli}@unisa.it

2. Context and Motivation
• Influence Maximization (IM)
• The aim is to find a set of nodes (seeds) in a given
network (e.g., a graph) that can maximize the spread of
information through the network under certain diffusion
processes
• Crucial for viral marketing, opinion formation, etc. [1,2]
• Higher-order Interactions
• Interactions that involve three or more entities
simultaneously
• Social systems, neuroscience, ecology, biology, etc. [3]
• Best modeled via hypergraphs [4]
• A hypergraph consists of nodes and hyperedges
• Hyperedge = subset of nodes
• What about IM on hypergraphs?
• Only a bunch of approaches in the last years [5,6]

3. Influence Maximization on Hypergraphs
• Given a hypergraph 𝐻 = 𝑉, 𝐸 , a value 𝑘 ∈ ℤ>0, and a diffusion process 𝜎𝐻
• Find a subset 𝑆∗
⊆ 𝑉 of 𝑘 nodes such that the expected number of infected
nodes is maximized:
𝑆∗
= 𝑎𝑟𝑔𝑚𝑎𝑥𝑆⊆𝑉, 𝑆 =𝑘𝜎𝐻(𝑆)
• Expected influence 𝜎𝐻 𝑆
• The number of reached nodes at the end of the process 𝜎𝐻 starting from the seed set 𝑆
• We consider the Suceptible-Infected (SI) model with Contact Process (CP) [6]
• A node can be either in a susceptible (S) or infected (I) state,
• An S-node can be infected by each of its neighbors in I-state with probability 𝛽
• The process iterates for 𝑇 > 0 steps

4. Proposed Algorithms
• The SmartPROPS algorithm
• Sort nodes based on a node property function 𝜙: 𝑉 → ℝ
• Select the top-𝑘 candidate seeds based on a threshold
value 𝜌: 𝑉 → ℝ
• Avoids taking nodes with a high hyperedge overlap
• The HC algorithm
• A random-restart steepest ascent hill climbing-based
algorithm
• The ES algorithm
• An evolutionary strategy-inspired algorithm
• Four variants defined for each algorithm
• Two of them are based on the degree and
hyperdegree properties,
• Two of them consider cooperative game theoretic
centrality measures (degree and closeness) based on
the Shapley Value

5. Results
• Eight datasets, four baselines
• HC and ES always outperform baselines
• Shapley Value-based variants work consistently well

6. Conclusion
• We proposed two families of approaches for the IM problem on
hypergraphs
• Node properties-based approaches: SmartPROPS,
• Metaheuristics-based approaches: HC and ES
• All algorithms achieve solid performances and often outperform baselines
• Game-theoretic centrality measures are a very promising tool for addressing this
problem
• Future directions
• IM on temporal-evolving and large-scale hypergraphs
• IM variants on hypergraphs

7. Thanks for your attention!
These slides are available at https://bit.ly/imhg-aixia24
Francesco Cauteruccio
DIEM, University of Salerno
fcauteruccio@unisa.it
francescocauteruccio.info

8. Bibliography
[1] Kempe, D., Kleinberg, J., Tardos, E., 2003. Maximizing the spread of influence through a social network, in: KDD,
pp. 137–146
[2] Amoruso, M., Anello, D., Auletta, V., Cerulli, R., Ferraioli, D., Raiconi, A., 2020. Contrasting the spread of
misinformation in online social networks. Journal of Artificial Intelligence Research 69, 847–879. AI Access Foundation
[3] Battiston, F., Cencetti, G., Iacopini, I., Latora, V., Lucas, M., Patania, A., Young, J.G., Petri, G., 2020. Networks
beyond pairwise interactions: Structure and dynamics. Physics Reports 874, 1–92. Elsevier.
[4] Aksoy, S.G., Joslyn, C., Marrero, C.O., Praggastis, B., Purvine, E., 2020. Hypernetwork science via high-order
hypergraph walks. EPJ Data Science 9, 16. Springer.
[5] Xie, M., Zhan, X.X., Liu, C., Zhang, Z.K., 2023. An efficient adaptive degree-based heuristic algorithm for influence
maximization in hypergraphs. Information Processing & Management 60, 103161. Elsevier
[6] Gong, X., X., H.W., Wang, Chen, C., Zhang, W., Zhang, Y., 2024. Influence maximization on hypergraphs via multi-
hop influence estimation. Information Processing & Management 61, 103683. Elsevier

9. Extra: Experiments