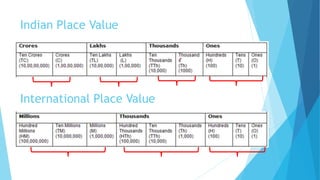
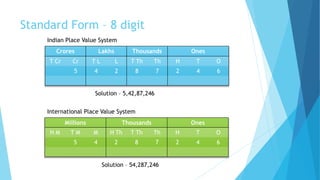
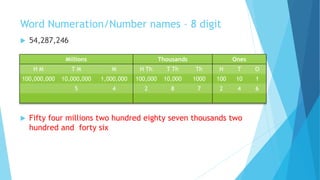
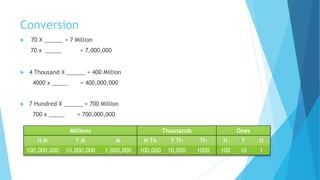
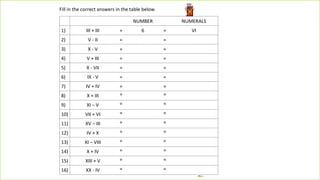
This document provides information about large numbers and place value systems. It covers topics like place value, the Indian and international place value systems, expanded and standard forms for writing numbers, and rounding numbers to the nearest ten, hundred or thousand. It also includes information about the largest and smallest numbers for a given number of digits. Roman numerals and their values are defined at the end.

1. Large Numbers
Grade 5
Nisha Mahajan

2. Topics Covered
 Place Value – Value of a number according to it Place
 Face Value – Absolute value of a number i.e. Digit.
 Indian Place Value system
 International Place Value System
 8 digit number
 Numeration of a number - Indian and International place value
 Long Expanded form
 Short Expanded form
 Standard form

3. Place Value
Q . Write the place value of 2 in:
a) 5428 b) 7246
Th H T O Th H T O
5 4 2 8 7 2 4 6
Ans . 20 Ans. 200

4. Indian Place Value
International Place Value

5. Standard Form – 8 digit
Crores Lakhs Thousands Ones
T Cr Cr T L L T Th Th H T O
5 4 2 8 7 2 4 6
Millions Thousands Ones
H M T M M H Th T Th Th H T O
5 4 2 8 7 2 4 6
Indian Place Value System
International Place Value System
Solution – 5,42,87,246
Solution – 54,287,246

6. Word Numeration/Number names – 8 digit
 54,287,246
 Fifty four millions two hundred eighty seven thousands two
hundred and forty six
Millions Thousands Ones
H M T M M H Th T Th Th H T O
100,000,000 10,000,000 1,000,000 100,000 10,000 1000 100 10 1
5 4 2 8 7 2 4 6

7. Expanded Form – 8 digit
 54,287,246
 Long Expanded Form
(5 x 10,000,000) + (4 x 1,000,000) + (2 x 100,000) + (8 x 10,000) + (7 x 1000)
. + (2 x 100) + (4 x 10) + (6 x 1)
 Short Expanded Form
50,000,000 + 4,000,000 + 200,000 + 80,000 + 7,000 + 2000 + 40 + 6
Millions Thousands Ones
H M T M M H Th T Th Th H T O
100,000,000 10,000,000 1,000,000 100,000 10,000 1000 100 10 1
5 4 2 8 7 2 4 6

8. Expanded Form – 9 digit
 154287246
 Standard Form 154,287,246
 Word/Number Name : One hundred fifty four millions two hundred eighty seven thousands
two hundred and forty six
 Long Expanded Form
(1 x 100,000,000) + (5 x 10,000,000) + (4 x 1,000,000) + (2 x 100,000)
+ (8 x 10,000) + (7 x 1000) + (2 x 100) + (4 x 10) + (6 x 1)
 Short Expanded Form
100,000,000 + 50,000,000 + 4,000,000 + 200,000 + 80,000 + 7,000 + 2000 + 40 + 6
Millions Thousands Ones
H M T M M H Th T Th Th H T O
100,000,000 10,000,000 1,000,000 100,000 10,000 1000 100 10 1
1 5 4 2 8 7 2 4 6

9. Largest and Smallest number
 Smallest 8 digit number – 10,000,000
 Largest 8 digit number – 99,999,999
 Smallest 9 digit number – 100,000,000
 Largest 9 digit number – 999,999,999
Fun Fact
 Largest n digit number + 1 = smallest n+1 digit number
Eg. largest 8 digit number = smallest 9 digit number
i.e. 99,999,999 + 1 = 100,000,000

10. Building greatest and smallest numbers
 To get greatest number , we arrange the digits in descending order.
Eg. 7 ,2, 0 , 1 , 8 , 3 , 4
8 7 4 3 2 1 0
 To get the smallest number , we arrange the digit in ascending order. ( we do
not place 0 at extreme left )
Eg. 7 ,2, 0 , 1 , 8 , 3 , 4
1 0 2 3 4 7 8

11. Homework
 Write the following in place value chart:
a) 48374951 b) 200091386 c) 165329814
 Write the following numbers in standard form and in words:
a) 325102014 b) 700000008 c) 6839205
 Write the following numbers in short expanded form:
a) 47392469 b) 789542370
 Write the Successor of
a) Greatest 7 digit number
b) Smallest 6 digit number

12. Homework
 Write the Successor of
a) Smallest 9 digit number
b) Greatest 8 digit number
 Write the greatest and smallest 7 digit number using ( without repeating the
digits)
A) 4, 7 , 6 , 3 , 2 , 9 and 1 B) 2, 5 , 6 , 0 , 4 , 3 and 7
 Find place value of
a) 2 in 523,567,986 b) 1 in 170,364 c) 7 in 876,892,046
 Write the following number in figures
a) Three hundred fifteen thousand , four hundred nineteen
b) Thirty two million four hundred seventy five thousand four

13. Successor
 Successor of number is one more than the number.
 Eg. 567,892,876
Successor – 567,892,876 + 1 = 567,892,877
Predecessor
 Predecessor of number is one less than the number.
 Eg. 567,892,876
Successor – 567,892,876 - 1 = 567,892,875
Fun Fact –
Successor of Largest n digit number + 1 = smallest n+1 digit number
Eg. Successor of largest 6 digit number = smallest 7 digit number
i.e. 999,999 + 1 = 1,000,000

14. Conversion
 70 X ______ = 7 Million
70 x _____ = 7,000,000
 4 Thousand X ______ = 400 Million
4000 x _____ = 400,000,000
 7 Hundred X ______ = 700 Million
700 x _____ = 700,000,000
Millions Thousands Ones
H M T M M H Th T Th Th H T O
100,000,000 10,000,000 1,000,000 100,000 10,000 1000 100 10 1

15. Comparing large number
 Number with more digit is greater .
Eg. 76,089,364 > 9,735,367
 If both numbers have equal no. of digits, then the number with the greatest
digit in largest place is greater.
Eg. 76,089,364 < 98,735,367
76,098,653 < 76,099,763

16. Practice
 Find the successor of :
1. 9,825,799
2. 19,999,999
3. Greatest 7 digit number
 Find the predecessor of
1. 73,500,000
2. 98,563,110
3. Smallest 8 digit number
 Write the greatest and the smallest 6 digit number , without repetition
1. 2 , 9 , 3 , 6 , 1 , 5
2. 7 , 2 , 8 , 0 , 1 , 1

17. Practice
 Complete the pattern
1. 534,027 , 534,127 , 534,227, _______, _______, ______.
2. 4,312,563, 4,322,563, 4,332,563, _______, ______, _______.
 Compare
1. 357,412 _____ 1,541,378
2. 35,192,570 _____31,927,053
3. 87,378,839 _____ 87,378,840
4. 927,278 _____ 927,179

18. Rounding off number nearest 10
1. We replace the digit in ones place by 0.
2. If the unit or ones place is > 5 , we increase the digit in tens place by 1 else make
no change.
Eg. 2546
Here 6 > 5 , there for we will replace ones place i.e. 6 by 0 and increase tens place
digit i.e. 4 by 1
Ans – 2550
Eg. 2543
Here 3 < 5 , there for we will replace 3 by 0
Ans – 2540
Q. Round off to nearest 10.
a) 73 b) 145 c) 295 d) 3,244 e) 51,766

19. Rounding off number nearest 100
1. We replace the digit in tens and ones place by 00.
2. If the tens place is > 5 , we increase the digit in hundreds place by 1, else make
nu changes
Eg. 2543
Here 4 < 5 , there for we will replace tens and ones place by 00
Ans – 2500
Eg. 2563
Here 6 > 5 , there for we will replace tens and ones place by 00 and increase hundreds
place digit i.e. 5 by 1
Ans – 2600
Q.Round off to nearest 100
a) 263 b) 1350 c) 4731 d) 5660 e) 32,892

20. Rounding off number nearest 1000
1. We replace the digit in hundreds ,tens and ones place by 000.
2. If the hundreds digit is > 5 , we increase the digit in thousands place by 1, else
make n0 changes
Eg. 25430
Here 4 < 5 , there for we will replace hundreds , tens and ones place by 000
Ans – 25000
Eg. 25630
Here 6 > 5 , there for we will replace hundreds, tens and ones place by 000 and
increase thousands place digit i.e. 5 by 1
Ans – 2600
Q. Round of to nearest 1000
a) 971 b) 3501 c) 8489 d) 29,604 e) 599,512

21. Practice
1. A 3-digit number was rounded off to the nearest hundred and the result was
600. Find the interval of the original number.
Solution :
Each number from 550 to 599 can be rounded off to 600
Each number from 601 to 649 can be rounded of as 600.
So, interval of the original number is 550 to 649

24. Roman Numerals
I V X L C D M
1 5 10 50 100 500 1000
 There are no roman numerals for 0.
 When a symbol is repeated , the value of roman number = Value of
roman numeral X times it is repeated
Eg. I I = 1 X 2 = 2
X X = 10 X 2 = 20
 Symbols V , L and D are never repeated.
X = 10 and not VV

25. Roman Numerals
I V X L C D M
1 5 10 50 100 500 1000
 If a numeral is written to right of another symbol of greater value,
the value of numbers is sum of value of symbols.
Eg. X I = 10 + 1 = 11
V I = 5 + 1 = 6
 If a numeral is written to left of another symbol of greater value, the
value of numbers is difference of value of symbols.
Eg. I X = 10 - 1 = 9
I V = 5 - 1 = 4

26. Roman Numerals
I V X L C D M
1 5 10 50 100 500 1000
 If symbols are combined, the value of smaller symbol in middle of
two greater symbol is subtracted from value of symbol on the right.
Eg. X I V = 10 + ( 5 -1) = 14
X X X I X = 10 + 10 + 10 + ( 10 – 1) = 39