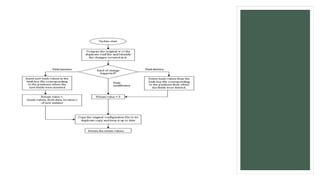
The document describes a hash-based inventory system that uses hashing algorithms to create a list of inventory parts and quantities sold. The system has three modules: constructing a hash table, searching for inventory items by generating hash codes, and generating reports of parts and quantities. It discusses hash tables, hashing functions, and basic hash table operations like search, insert, and delete. The document also provides examples of hash functions and how they map strings to indexes in a hash table to enable fast retrieval of data.

1. HASH BASED
INVENTORY
SYSTEM

2. • Description: The main aim of this project is to implement a hashing algorithm to create a list of
• inventory parts and their quantities sold. There are three modules in this project
• Construction of hash table: HASH tables are widely used to quickly search and retrieve
• information from enormous amounts of data. In this for spare part code its code is taken and
• Search for an inventory item: In this the user has enter spare part code, it generates
• hash codrespectivee to access respective spare part record and prints that record indicates its quantity
• Reports: In this module it has to generate a complete report of spare parts and their quantity
• sold.
• generates hash code and spare part record to search retrieve.

3. • Requirements: To implement this project student should have knowledge on
• Indexing
• Hash tables
• Hashing functions
• Hash Table is a data structure which stores data in an associative manner. In a hash table, data
stored in an array format, where each data value has its own unique index value. Access of
becomes very fast if we know the index of the desired data.
• Thus, it becomes a data structure in which insertion and search operations are very fast
irrespective of the size of the data. Hash Table uses an array as a storage medium and uses
technique to generate an index where an element is to be inserted or is to be located from.

4. • HASHING:
• Hashing is a technique to convert a range of key values into a range of indexes of an array.
We're going to use modulo operator to get a range of key values.
• Basic Operations
• Following are the basic primary operations of a hash table.
• Search − Searches an element in a hash table.
• Insert − inserts an element in a hash table.
• delete − Deletes an element from a hash table.

5. • Search Operation
• Whenever an element is to be searched, compute the hash code of the key passed and locate
the element using that hash code as index in the array. Use linear probing to get the element
ahead if the element is not found at the computed hash code.
• Insersion operation
• Whenever an element is to be inserted, compute the hash code of the key passed and locate the
index using that hash code as an index in the array. Use linear probing for empty location, if an
element is found at the computed hash code.
• Delete Operation
• Whenever an element is to be deleted, compute the hash code of the key passed and locate the
index using that hash code as an index in the array. Use linear probing to get the element ahead
if an element is not found at the computed hash code. When found, store a dummy item there
to keep the performance of the hash table intact.

6. • Hashing is implemented in two steps:
• An element is converted into an integer by using a hash function. This element can be used as
an index to store the original element, which falls into the hash table.
• The element is stored in the hash table where it can be quickly retrieved using hashed key.
• hash = hashfunc(key)
• index = hash % array_size
• In this method, the hash is independent of the array size and it is then reduced to an index (a
number between 0 and array_size − 1) by using the modulo operator (%).

7. • Hash function
• A hash function is any function that can be used to map a data set of an arbitrary size to a data set
a fixed size, which falls into the hash table. The values returned by a hash function are called hash
values, hash codes, hash sums, or simply hashes.
• To achieve a good hashing mechanism, It is important to have a good hash function with the
following basic requirements:
• Easy to compute: It should be easy to compute and must not become an algorithm in itself.
• Uniform distribution: It should provide a uniform distribution across the hash table and should not
result in clustering.
• Less collisions: Collisions occur when pairs of elements are mapped to the same hash value. These
should be avoided.
• Note: Irrespective of how good a hash function is, collisions are bound to occur. Therefore, to
maintain the performance of a hash table, it is important to manage collisions through various
collision resolution techniques.

8. • Here, it will take O(n) time (where n is the number of strings) to access a specific string. This
shows that the hash function is not a good hash function.
• Let’s try a different hash function. The index for a specific string will be equal to sum of ASCII
values of characters multiplied by their respective order in the string after which it is modulo
with 2069 (prime number).

9. • String Hash function Index
• abcdef (971 + 982 + 993 + 1004 + 1015 + 1026)%2069 38
• bcdefa (981 + 992 + 1003 + 1014 + 1025 + 976)%2069 23
• cdefab (991 + 1002 + 1013 + 1024 + 975 + 986)%2069 14
• defabc (1001 + 1012 + 1023 + 974 + 985 + 996)%2069 11
• Hash table
• A hash table is a data structure that is used to store keys/value pairs. It uses a hash function to
compute an index into an array in which an element will be inserted or searched. By using a
good hash function, hashing can work well. Under reasonable assumptions, the average time
required to search for an element in a hash table is O(1).