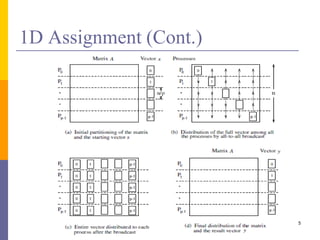
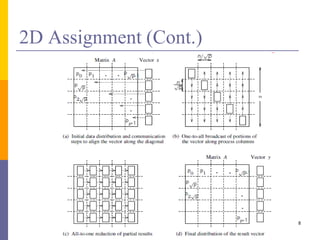
The document discusses several problems that are hard to parallelize, including matrix-vector multiplication and matrix-matrix multiplication. It describes 1D and 2D assignment approaches to parallelizing matrix-vector multiplication across multiple processors. 1D assignment distributes the rows of the matrix and vector across processors, while 2D assignment distributes them in a 2D grid. It also outlines map-reduce approaches to parallelizing vector-matrix and matrix-matrix multiplication, breaking the problems into mapping and reducing stages.

1. Hard to Parallelize Problems
CS5225 Parallel and Concurrent Programming
Dilum Bandara
Dilum.Bandara@uom.lk
Some slides adapted from Dr. Srinath Perera

2. Problems
 Matrix-Vector Multiplication
 1D assignment
 2D Assignment
 Matrix-Matrix Multiplication
2

3. Matrix-Vector Multiplication
 If x is copied to all processors, parallel solution is trivial
 Assign each row to a processor & calculate, & reduce to output
results
 Expensive if read vector from a file
 Alternatives
 Each process reads parts of data & writes part of the results
 1D & 2D Assignment
3

4. 1D Assignment
 Each processor is given a row
 Vector is broken down between processors
 Vector is distributed to all through processor via all-to-
all broadcast
 Each vector writes its part of the results
4

5. 1D Assignment (Cont.)
5

6. 1D Assignment – MPI Based
Implementation
 For i-th process
a[i] = read(a[i]); //read row i
x = read(x[i]); //read part of vector
MPI_allgather(x, allx);
y = CalculateY(a[i], allx);
Write(y);
6

7. 2D Assignment
 Distributed across n2 processors & vector is
distributed across leftmost n processors
 Solution
 Each (i, n)-th processor sends to (i, i) processor
 Each (i, i) processor broadcasts over the column
 Calculates results
 Reduce results across rows
7

8. 2D Assignment (Cont.)
8

9. 2D Assignment (Cont.)
For (i, j)-th process
a[x][y] = read(a[x][y]);
If(j == n)
x = read(x[i]);
MPI_Send(x, (i, i))
If(i == j){
MPI_Receive(&block)
MPI_Broadcast(block, j);
blockRecv = block;
}
else{ //receive block from others
MPI_Broadcast(&block, 1, &blockRecv, 1, (j, j));
}
y(I, j ) = Calculate();
//reduce it at the 0th on earch row
MPI_REDUCE(y(I, j), 1, &resultrcv, 1, (i, 0));
write(&resultrcv);
9

10. Vector-Matrix Multiplication with
Map-Reduce
 If vector fits in memory
 Map
 Send vector & a row to each map task & send to (i, result)
 Reduce
 Print final results
10

11. Vector-Matrix Multiplication with
Map-Reduce (Cont.)
 If vector does not fit in memory
 Use 1D or 2D Assignments depending on size
 Map
 Send vector & a row to each map task & send to (i, result)
 If it doesn’t fit
 Send part of vector & part of row to each map task & send to (i,
result)
 Reduce
 Print final results
 Refer to “2.3.1 Matrix-Vector Multiplication by Map-
Reduce” in the Mining large data sets book
11

12.  Map
 Make (key, value) pairs out of matrices mij & njk
 Produce (j, (M, i, mij) and (j, (N, k, njk)
 Reduce
 Produce for each j (j, (i, k, mij, njk))
 Map again
 Produce [((i1, k1), m1j*nj1), ((i2, k2), m2j*nj2), …, ((ip, kp), mpj*njp)]
 Reduce again
 For each (i, k) pair sum all & produce ((i, k), v)
Matrix-Matrix Multiplication
12