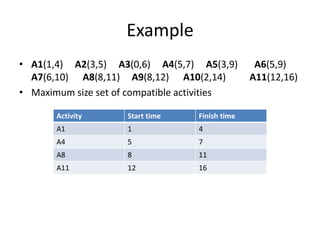
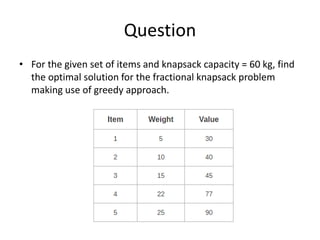
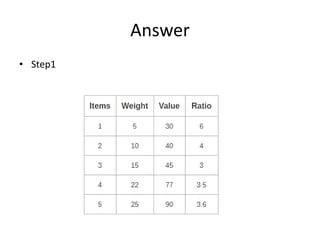
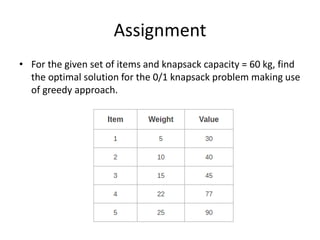
The document discusses various greedy algorithms and optimization problems. It explains that greedy algorithms make locally optimal choices at each step to arrive at a global solution. An example of an activity selection problem is provided where activities are scheduled greedily based on their finish times. The fractional knapsack problem is also summarized, where the greedy approach is to fill items in order of their value to weight ratio until the knapsack is full.

1. Greedy Approach

2. Brute Force
• Brute force approach is a straight forward approach to solve
the problem. It is directly based on the problem statement
and the concepts
• It is one of the simplest algorithm design to implement and
covers a wide range of problems under its gamut.
• Closest pair problem
• NC2 pairs.
• For each pair find distance.
• Find the minimum
• No clever thinking, no strategy

3. Optimization Problem
• Some problems may have more than one solutions.
• An optimization algorithm is a procedure which is executed
iteratively by comparing various solutions till an optimum or a
satisfactory solution is found.
• A optimization algorithm procedure aims to find the optimal
solutions to the objective function or functions under
constraints.

4. Greedy Method
• Greedy design technique is primarily used in Optimization
problems
• The Greedy approach helps in constructing a solution for a
problem through a sequence of steps where each step is
considered to be a partial solution.
• A greedy algorithm always makes the choice that looks best
at the moment.
• The choice of each step in a greedy approach is done based
on the following
– It must be feasible
– It must be locally optimal
– It must be irrevocable

5. Greedy Method
• In the greedy approach each step chosen has to satisfy the
constraints given in the problem.
• Each step is chosen such that it is the best alternative among
all feasible choices that are available.
• The choice of a step once made cannot be changed in
subsequent steps.
• This heuristic strategy does not always produce an global
optimal solution.

6. An activity-selection problem
• Schedule a set of competing activities that needs exclusive
use of a common resource.
• Each activity ai has start time si and finish time fi.
• 0 <= si < fi < ∞
• Activity ai and aj are compatible if the interval [si , fi) and [sj , fj)
do not overlap.
• Goal- to select maximum size subset of mutually compatible
activities.
• f1<= f2<= f3 <= ...... <= fn-1 <= fn

7. Making the greedy choice
• If we make the greedy choice, we have only one remaining
subproblem to solve: finding activities that start after a1
finishes.

8. Recursive Algorithm
• The initial call, which solves the entire problem, is RECURSIVE-
ACTIVITY-SELECTOR(s, f, 0, n).

9. Iterative Algorithm

10. Example
• A1(1,4) A2(3,5) A3(0,6) A4(5,7) A5(3,9) A6(5,9)
A7(6,10) A8(8,11) A9(8,12) A10(2,14) A11(12,16)
• Maximum size set of compatible activities
Activity Start time Finish time
A1 1 4
A4 5 7
A8 8 11
A11 12 16

11. Fractional Knapsack problem
• We are given n objects and a knapsack. Object i has weight wi
and benefit value bi. The knapsack has a capacity W.
• if a fraction xi, 0<= xi <= 1 of object i is placed into the
knapsack then a benefit value of bixi is earned.
• The objective is to obtain a filling of the knapsack that
maximizes the total benefit earned.
• Since the knapsack capacity is W, the total weight of all
chosen objects should be W. The benefits & weights are
positive.

13. Procedure
• Step 1
For each item, compute its value / weight ratio.
• Step 2
Arrange all the items in decreasing order of their value /
weight ratio.
• Step 3
Start putting the items into the knapsack beginning from the
item with the highest ratio.
Put as many items as you can into the knapsack.
• Time complexity depends upon the sorting algorithm’s
running time.

14. Question
• For the given set of items and knapsack capacity = 60 kg, find
the optimal solution for the fractional knapsack problem
making use of greedy approach.

15. Answer
• Step1

16. • Step2
Items in decreasing order of their ratio
I1, I2, I5, I4, I3
• Step3
Start filling the knapsack by putting the items into it one by one.
I1(5,30), I2(10,40), I5(25,90) I4(20, 20/22 * 77)
Now total weight = 5 + 10 + 25 + 20= 60
maximum benefit value = 30 + 40 + 90 + 70 = 230

17. Assignment
• For the given set of items and knapsack capacity = 60 kg, find
the optimal solution for the 0/1 knapsack problem making use
of greedy approach.