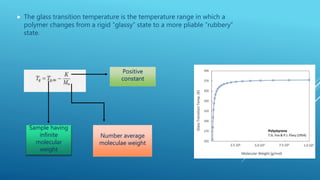
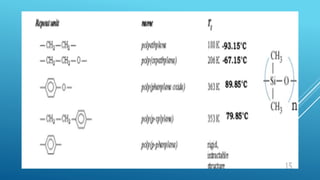
The glass transition temperature of polymers is affected by several factors: 1. Molecular weight - Higher molecular weight polymers have lower mobility and higher glass transition temperatures due to increased entanglement between chains. The Fox equation models this relationship. 2. Chain flexibility - More flexible polymer chains with fewer steric hindrances, like polydimethylsiloxane, have lower glass transition temperatures due to increased mobility. 3. Intermolecular interactions - Stronger interactions between polymer chains increase molecular crowding and packing, raising the glass transition temperature. Changes to polymer structure can alter these interactions and the transition temperature.

1. GLASS TRANSITION TEMPRATURE
Enrollment no:- 190280126039
Enrollment no:- 190280126033
Enrollment no:- 190280126035
Enrollment no:- 190280126029
Enrollment no:- 190280126034
Enrollment no:- 190280126017
Enrollment no:- 190280126030
Enrollment no:- 190280126014
PROF.GANNU BHATT

2. SOME FACTORS AFFECTING GLASS TRANSITION
TEMPERATURE
 Chain flexibility
 Intermolecular interactions
 Molecular weight
 Co polymerization
 Cross-linking
 plasticizer

3. 1. MOLECULAR WEIGHT
Molecular weight: Polymer having low molecular weight has more number of chain ends in
compare of polymer having high molecular weight. Chain ends have less strain and become
more active than the chain backbone and causes greater molecular mobility. Therefore
increase in molecular weight decreases the glass transition temperature of polymer and it is
reasonable to assume that with increase of chain-end concentration glass transition
temperature increases linearly on the other hand we can say that glass transition
temperature decreases linearly with increase of molecular weight of polymer. Equation
given below relates the glass transition temperature of polymer with its molecular weight,
Tg=T∞g - K(1/Mn)
T∞g is the glass transition temperature of sample having infinite molecular weight, K is
positive constant and Mn is number average molecular weight.

4.  The glass transition temperature of amorphous and fractionated poly(ethylene
terephthalate) has been measured by differential scanning calorimetry. The
application of the Fox-Flory equation for the range of molecular weights between
37100 and 4500 gives the values of Tg∞=342.4 K.
The Flory–Fox equation relates the number-average molecular weight, Mn, to the glass
transition temperature, Tg, as shown Below:
1/Tg= w1/Tg1 + w2/Tg2
where Tg,∞ is the maximum glass transition temperature that can be achieved at a
theoretical infinite molecular weight and K is an empirical parameter that is related to
the free volume present in the polymer sample. It is this concept of “free volume” that is
observed by the Flory–Fox equation.

5.  The glass transition temperature is the temperature range in which a
polymer changes from a rigid “glassy” state to a more pliable “rubbery”
state.
Sample having
infinite
molecular
weight
Positive
constant
Number average
moleculae weight

6.  A High molecular weight increases the impact resistance of the material. The higher
degree of entanglement means that in order to rupture, more polymer bonds need to be
broken, this means that the polymer can absorb more energy before failing. A
High molecular weight increases the chemical resistance.
 X= -CH3 Polypropylene Tg = 253K = -20.15C
-Cl poly(vinyl chloride) 354K = 80.85C
-OH Poly(vinyl alcohol) 358K = 84.85C
Low molecular weight values result in lower glass transition temperature whereas increasing
value of molecular weight result in an asymptotic approach of the glass transition
temperature to tg(infinity).
For a given molecular weight of the polymer, a low molecular weight sample will have more
chain end segment than a high molecular weight sample.
The larger the number of chain and segment, the larger will be the effective segmental
motion.

7.  In short chain ends can be viewed as an “ impurity ” when considering
the packing of chains and more impurity results in a lower Tg .
 Thus, glass transition temperature is dependent on free volume which
is turn is dependent on the average molecular weight of the polymer
sample. This relationship is described by the Flory-fox equation.
 These can be done by controlling cooling rate and isothermal time
during heat treatment, and polymer modification, respectively. On the
other hand, increasing pressure to polymer will also increase
molecular crowing and interaction, resulting increased Tg.

8. CHAIN FLEXIBILITY& RIGIDITY
 As Tg depemdson the ability of a chain to undergo internal rotations, we expect chain
flexibility to be associated with low glass transitions.
 For example, poly(dimethyl siloxane) is an extremely flexible polymer due to the
large separation between the methyl substituted silicon atoms. As compared to other
polymeric materials, poly(dimethyl siloxane) has the lowest glass transition
temperature (Tg = -123.15C)
 The value of Tg depends on the mobility of the polymer chain, and for most synthetic
polymers lies between 170 K to 500 K. The transition from the glass to the rubber-like
state is an important feature of polymer behavior, marking a region of dramatic
changes in the physical properties, such as hardness and elasticity.

9.  Dependence of the glass-transition temperature, Tg, on polymer chain flexibility
predicted by the Gibbs-DiMarzio theory was empirically tested by studying the
relationship between Tg and the stiffness parameter for isolated chains, .
 It was found that is not a single variable controlling Tg for different polymer series
which have different free volume fractions at Tg as a result of intrinsic differences in
packing density in the crystalline state.
 The results obtained suggest that Tg of linear polyethylene lies near 160°K. A
functional form of dependence of Tg on chain stiffness parameter and on local chain
packing coefficient at Tg is proposed.