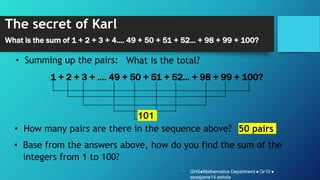
This document describes a famous story about the German mathematician Karl Friedrich Gauss. When Gauss was 10 years old, his teacher posed the question "What is the sum of 1 + 2 + 3 + ... + 98 + 99 + 100?" to the class. Gauss immediately wrote down the correct answer without showing any working. The document then provides additional context about Gauss and his shortcut formula to solve the problem, as well as examples of using the formula to find sums of arithmetic sequences.

1. The secret of Karl
What is the sum of 1 + 2 + 3 + 4…. 49 + 50 + 51 + 52… + 98 + 99 + 100?
This is a famous story of Karl Friedrich Gauss (1777-1885), a German mathematician, is renowned
for his varied contributions to the field of mathematics and physics. When Gauss was ten years old, he
was permitted to attend Mr. Buttner’s arithmetic class. Teacher Buttner was known for being cynical
and having little respect for the peasant children he was teaching. The teacher had written on the
board the question above to keep the children busy and so that they might appreciate the “shortcut”
formula he was preparing to teach them. Gauss took one look at the problem, for seconds he invented
the shortcut formula on the spot, and immediately wrote down the correct answer.
• The challenge now, can you beat this 10-year-old Gauss? What do you think was his answer?
• Do you know how he did it?
• GHS●Mathematics Department ● Gr10 ●
aaadjame14.estiola

2. The secret of Karl
What is the sum of 1 + 2 + 3 + 4…. 49 + 50 + 51 + 52… + 98 + 99 + 100?
• Summing up the pairs:
1 + 2 + 3 + …. 49 + 50 + 51 + 52… + 98 + 99 + 100?
101
What is the total?
• How many pairs are there in the sequence above? 50 pairs
• Base from the answers above, how do you find the sum of the
integers from 1 to 100?
• GHS●Mathematics Department ● Gr10 ●
aaadjame14.estiola

3. SUM OF ARITHMETIC Sequence
OBJECTIVES:
1. Discuss how to determine the sum of an arithmetic sequence
2. Find the sum of an arithmetic sequence
1 + 2 + 3 + …. 49 + 50 + 51 + 52… + 98 + 99 + 100?
• GHS●Mathematics Department ● Gr10 ●
aaadjame14.estiola
ALLEN M. ESTIOLA
Master Teacher I, GUN-OB HS, LLC Division

4. SUM OF ARITHMETIC Sequence
The formula for the SUM of an Arithmetic Sequence is
where: S = the sum of an Arithmetic sequence
n = the number of terms
a1 = the 1st term
d = the common difference
Sn =
𝒏
𝟐
[2a1 + (n – 1)d] Sn =
𝒏
𝟐
[a1 + an]
an = the last term
• GHS●Mathematics Department ● Gr10 ●
aaadjame14.estiola

5. ILLUSTRATIVE EXAMPLES
Find the sum
of the first 70
terms of the
arithmetic
sequence if
the first term
is 22 and the
twentieth
term is 155?
22, … 155, … a70,
S1 Given: a1 = 22
n = 20
S2 Find: d,
S4 Solve for S70 using the formula
S70 =
70
2
[2(22) + (70 – 1)(7)]
Sn =
𝑛
2
[2a1 + (n – 1)d]
S70 = 35[44 + (69)(7)]
S70 = 35[44 + 483]
S70 = 35[527]
S70 = 18 445
S5 Therefore the sum of the 1st 70
terms is 18 445.
a20 = 155 
n = 70
S70
S3 Find d
an = a1 + n − 1 d
𝑎20 = 22 + 20 − 1 𝑑
155 = 22 + 19𝑑
155 − 22 = 19𝑑
133 = 19𝑑
𝑑 = 7
GHS●Mathematics Department ● Gr10 ●

6. ILLUSTRATIVE EXAMPLES
A conference hall
has 10 rows of
seats. The first row
contains 30 seats,
the second row
contains 42 seats,
the third row
contains 54 seats,
and so on. Find the
total number of
seats in the
conference hall.
30, 42, 54, …
S1 Given: a1 = 30
d = 12
n = 10
S2 Find: S10
S3 Solve for S10 using the formula
S10 =
10
2
[2(30) + (10 – 1)(12)]
Sn =
𝑛
2
[2a1 + (n – 1)d]
S10 = 5[60 + (9)(12)]
S10 = 5[60 + 108]
S10 = 5[168]
S10 = 840
S4 Therefore the total number of
seats in the conference hall is 840.
• GHS●Mathematics Department ● Gr10 ●
aaadjame14.estiola
Given:

7. ILLUSTRATIVE EXAMPLES
Find the indicated partial sum of the given sequence.
1. 4, 7, 10, 13, … S10
2. 13, 9, 5, 1, … S8
Find the sum of the first 20 terms of the arithmetic
sequence 4, 9, 14, 19, …

8. Application
SET A. A group of hikers has a trek of
10 hours to reach Mt. Manunggal.
They traveled 25km on the 1st hour, 23
km on the 2nd hour, 21 on the 3rd hour,
and so on. How many kilometers did
they travel to reach Mt. Manunggal?
• GHS●Mathematics Department ● Gr10 ●
aaadjame14.estiola
SET B. A househelp receives a salary
of 36 000php a year with contract of
250 annual increase of 7 years. What
is his total income for 7 years?

9. Assessment
A gardener plans to construct a trapezoidal-shape
garden. The longer side of the trapezoid needs to start
with a row of 99 bricks. Then 3 bricks will be decreased
on the succeeding row on each end and the construction
should stop at 26th row. How many bricks does he need
to purchase?
• GHS●Mathematics Department ● Gr10 ●
aaadjame14.estiola

10. Assignment
Study and prepare for a Long test tomorrow
• Generating the general rule
• Arithmetic Sequence
• Arithmetic Mean
• Sum of Arithmetic Sequence
• GHS●Mathematics Department ● Gr10 ●
aaadjame14.estiola