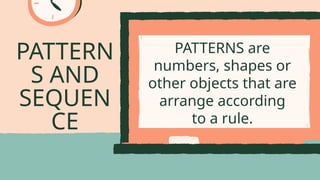
The document discusses generating and generalizing patterns and sequences, providing examples of both finite and infinite sequences. It poses various pattern continuation questions and defines a sequence as a function with its terms defined by specific rules. Examples include counting numbers and multiples, as well as patterns related to numbers and shapes.

1. GENERATING
PATTERNS
GENERATE AND GENERALIZE PATTERNS

2. Can you share your ideas?
WHAT COMES NEXT?
A B A B ?

3. Can you share your ideas?
WHAT COMES NEXT?
A B A B ?

4. Can you share your ideas?
What will be the next
figure?

5. ANSWER
What will be the next
figure?

6. Can you share your ideas?
What will be the next
figure?

7. ANSWER
What will be the
next figure?

8. 6, 12, 18, 24, ...
What will be the next
number in this
pattern?

9. 6, 12, 18, 24, 30
Each number in the
pattern is a multiple of
6.

10. 48, 24, 12, 6, ...
What will be the next
number in this
pattern?

11. 48, 24, 12, 6, 3
Each number in the
pattern is being halved.

12. TRY THIS ONE!
What is the next number?
What is the 8th
number?
X, Y, XX, YY, XXX, _____

13. TRY THIS ONE!
What is the next number?
What is the 7th
number?
1, 3, 9, 27, 81, _____

14. Find the next two terms of each sequence.
TERMS OF A SEQUENCE
TRY THIS!
a. 5, 8, 11, 14, ____, ____
b. 15, 7, -1, -9, ____, ____
c. 7, 14, 28, 56, ____, ____
d. 24, -12, 6, -3, ____, ____

15. HOW
DO
PATTER

16. PATTERN
S AND
SEQUEN
CE
PATTERNS are
numbers, shapes or
other objects that are
arrange according
to a rule.

17. WHAT IS SEQUENCE?
A sequence is a function whose domain
is the finite set{1,2,3,…, }
𝑛
or the infinite set {1,2,3,…}.
IT IS A CHAIN OF NUMBERS THAT USUALLY
FOLLOW A PARTICULAR PATTERN.
THE INDIVIDUAL ELEMENTS IN A SEQUENCE ARE
CALLED TERMS.

18. FINITE AND INFINITE
SEQUENCES
A sequence is infinite if its domain is the
set of positive integers without a last term,
{1, 2, 3, 4, …}. The three dots shows that the
sequence goes on and on indefinitely.
Example:
1. Counting Numbers: {1, 2, 3, 4, 5, 6, 7, 8,
…}
2. Multiples of three: {3, 6, 9, 12, 15, 18, …}

19. FINITE AND INFINITE
SEQUENCES
A sequence is finite if its domain is the set
of positive integers, {1, 2, 3, 4, …n} which has
a last term, n.
Example:
1. Vowels in the alphabet : {a, e, i, o, u}
2. First 5 positive perfect squares: {1, 4, 9, 16, 25}

20. How about
getting the
100th
term
on the