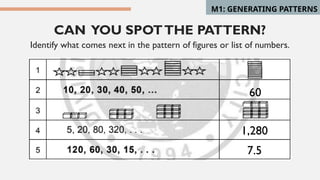
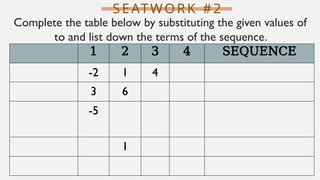
The document outlines the principles of generating patterns and sequences in mathematics, including finite and infinite sequences. It explains how to identify patterns, find the next term in a sequence, and determine the general or nth term of a sequence using mathematical rules. Examples illustrate the application of these concepts to solve problems involving sequences.