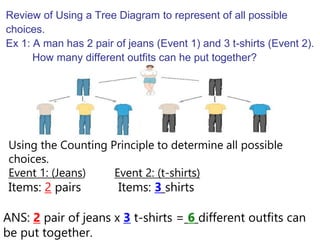
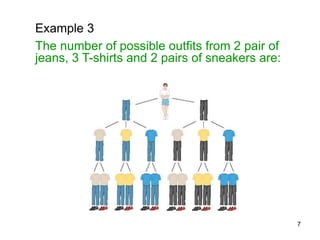
The document discusses the fundamental counting principle for determining the number of possible outcomes in a given situation. It provides examples of applying the principle to situations with two or more groups of items that can be chosen from. These include determining the number of possible outfits given various clothing items, the number of ways to order a two-course meal from menu options, and the number of possible schedules or multiple-choice test answers involving multiple choice groups. The principle states that if one event can occur in m ways and another in n ways, the number of ways both can occur is m×n, and if there are more than two groups, the counts are multiplied across all groups.

1. 2/19/2024 1
Notes #21
The Fundamental Counting Principle

2. 2/19/2024 2
Fundamental Counting Principle
How to Apply the Fundamental Counting Principle
ANS:
If you have 2 events: 1 event can occur “M” ways
and another event can occur “N” ways, then the
number of ways that both can occur is M∙N.
GOAL:
Use the Fundamental Counting Principle to
determine the number of possible outcomes in a
given situation.

3. Review of Using a Tree Diagram to represent of all possible
choices.
Ex 1: A man has 2 pair of jeans (Event 1) and 3 t-shirts (Event 2).
How many different outfits can he put together?
Using the Counting Principle to determine all possible
choices.
Event 1: (Jeans) Event 2: (t-shirts)
Items: 2 pairs Items: 3 shirts
ANS: 2 pair of jeans x 3 t-shirts = 6 different outfits can
be put together.

4. Example 2
Applying the Fundamental Counting Principle
The Greasy Spoon Restaurant offers 6 appetizers
and 14 main courses.
In how many ways can a person order a two
course meal?

5. Set up: (4 Steps)
1) Specify the Events
a) Event 1: Appetizers b) Event 2: Main courses
2) Indicate the # of items per Event
a. Event 1: 6 types of Appetizers b. Event 2: 14 main
courses
3) Apply the Counting Principle
6 appetizers x 14 main courses = 84
4) Answer in a complete sentence
ANS: Choosing from one of 6 appetizers and one of 14
main courses, a person has 84 ways to order a two-
course meal.

6. 2/19/2024 Section 11.1 6
The Fundamental Counting Principle with
More than Two Groups of Items
• Definition
3 events can occur m, n, & p ways, then the
number of ways all three can occur is m∙n∙p

7. 7
The number of possible outfits from 2 pair of
jeans, 3 T-shirts and 2 pairs of sneakers are:
Example 3

8. 2/19/2024 Section 11.1 8
Set up (4 Steps):
1) List the Events
a) Event 1: Jeans b) Event 2: T-Shirts
c)Event 3: Sneakers
2) List # of Items per Event
a) Jeans: 2 pair b) T-shirts: 3 shirts
c) Sneakers: 2 pair
3) Applying the Counting Principle
2 pair of jeans x 3 t-shirts x 2 pair of sneakers = 12 diff.
outfits
4) Concluding Sentence:
There are 12 different outfit that can be made.

9. 9
Example 4
Options in Planning a Course Schedule
Next semester, you are planning to take three
courses – Math, English and Humanities.
There are 8 sections of Math, 5 of English, and 4 of
Humanities that you find suitable.
Q: Assuming no scheduling conflicts, how many
different three-course schedules are possible?

10. 10
Example 4
Options in Planning a Course Schedule
Q: Assuming no scheduling conflicts, how many
different three-course schedules are possible?
Solution:
This situation involves making choices with three
groups of items.
Math English Humanities
{8 choices} {5 choices} {4 choices}
ANS: There are 8 ∙ 5 ∙ 4 = 160 diff. three-course
schedules.

11. 2/19/2024 Section 11.1 11
Example 5
Telephone Numbers in the United States
• Telephone numbers in the United States begin
with three-digit area codes followed by seven-
digit local telephone numbers.
- Area codes and local telephone numbers cannot
begin with 0 or 1.
Q: How many different telephone numbers are
possible?

12. 2/19/2024 Section 11.1 12
Telephone Numbers in the United States
Q: How many different telephone numbers are possible?
Solution:
This situation involves making choices with ten groups of
items. Here are the choices for each of the ten groups of
items:
CONDITION: Area codes and local telephone numbers cannot
begin with 0 or 1.
Area Code Local Telephone Number
The total number of different telephone numbers is:
8 ∙ 10 ∙ 10 ∙ 8 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 = 6,400,000,000
8 10 10 8 10 10 10 10 10 10

13. 2/19/2024 Section 11.1 13

14. 2/19/2024 Section 11.1 14
Example 5
Telephone Numbers in the United States
Q: How many different telephone numbers are possible?
Solution:
This situation involves making choices with ten groups of
items. Here are the choices for each of the ten groups of
items:
Area Code Local Telephone Number
8 10 10 8 10 10 10 10 10 10
The total number of different telephone numbers is:
8 ∙ 10 ∙ 10 ∙ 8 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 ∙ 10 = 6,400,000,000

15. 2/19/2024 Section 11.1 15
Example 5
A Multiple-Choice Test
• You are taking a multiple-choice test that has ten
questions. Each of the questions has four answer choices,
with one correct answer per question. If you select one of
these four choices for each question and leave nothing
blank, in how many ways can you answer the questions?
• Solution:
This situation involves making choices with ten questions:
Question 1 Question 2 Question 3 ∙ ∙ ∙ Question 9 Question 10
{4 choices} {4 choices} {4 choices} {4 choices} {4 choices}
The number of different ways you can answer the questions is:
4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 410 = 1,048,576