This document describes a new method for designing fuzzy controllers based on extending the classical Lyapunov synthesis method. The key points are: 1) The method assumes minimal knowledge about the plant and systematically derives the fuzzy rule base for the controller. 2) The method is demonstrated by designing Mamdani-type controllers for stabilizing and tracking an inverted pendulum system. The rule bases are derived analytically rather than heuristically. 3) Simulation results show the controllers achieve local stability of the closed-loop systems, even in the presence of noise, indicating the effectiveness of the new fuzzy Lyapunov synthesis method.

1. sets and systems
ELSEVIER
Fuzzy Sets and Systems 106 (1999) 49-59
Fuzzy Lyapunov-based approach to the design of fuzzy controllers
Michael Margaliot, Gideon Langholz*
Department o f Electrical Engineering - Systems, Tel Aviv University, Tel Aviv 69978, Israel
Received July 1998
Abstract
In this paper we extend the classical Lyapunov synthesis method to the domain of computing with words. This new
approach is used to design fuzzy controllers. Assuming minimal knowledge about the plant to be controlled, the proposed
method enables us to systematically derive the fuzzy rules that constitute the rule base of the controller. We demonstrate
the approach by designing Mamdani-type and Takagi-Sugeno-Kang-type fuzzy controllers for two well-known plants.
@ 1999 Elsevier Science B.V. All rights reserved.
Keywords: Lyapunov functions; Fuzzy control; Computing with words
1. Introduction
The most difficult aspect in the design of fuzzy controllers is the construction of the rule base [2]. The
process of extracting the knowledge of a human operator, in the form of fuzzy control rules, is by no means
trivial, nor is the process of deriving the rules based on heuristics and a good understanding of the plant and
control theory [7, 9].
We present a new method, based on extending the classical Lyapunov synthesis method to the design of
fuzzy controllers. We show that it enables us to systematically derive the fuzzy rule base. Basically, we
follow the classical Lyapunov synthesis method by constructing a Lyapunov function candidate V and then
determining the conditions required to indeed make it a Lyapunov function of the closed-loop system. It turns
out that, because we assume fuzzy knowledge about the plant to be controlled, the derived conditions can be
stated as fuzzy if-then rules.
We demonstrate our approach by applying it to the design of Mamdani-type stabilizing and tracking controllers for the inverted pendulum system, and by using it to design a Takagi-Sugeno-Kang-type controller
for regulating the water level in a water tank. It should be noted that controllers for these plants were already
synthesized by others (see, for example [1, 8]) using heuristics to derive the rule bases. In addition, properties
such as stability and robustness have also been demonstrated but only through simulations.
In contrast, we use the same examples in this paper to illustrate that our method can be used to derive the
rule bases analytically (rather than heuristically). We also believe that our approach might lead to an analytical
* Corresponding author. Tel.: + 9 7 2 3 6408764; fax: +972 3 6407095; e-mail: langholz@eng.tau.ac.il.
0165-0114/99/$ - see front matter @ 1999 Elsevier Science B.V. All rights reserved.
PII: S 0 1 6 5 - 0 1 1 4 ( 9 8 ) 0 0 3 5 6 - X

2. M. Margaliot, G. Langholz/Fuzzy Sets and Systems 106 (1999) 49-59
50
study of the stability and robustness of the resulting controllers. However, in this paper the emphasis is on
the presentation of the method and its use for deriving the rule bases.
The rest of this paper is organized as follows: In Section 2 we describe the new approach in detail.
In Section 3, we illustrate our approach by designing Mamdani-type stabilizing and tracking controllers for
the inverted pendulum system. In Section 4 we use it to design a Takagi-Sugeno-Kang-type controller for
regulating the water level in a water tank. The final section contains conclusions.
2. Fuzzy Lyapunov synthesis
In this section we describe the proposed fuzzy Lyapunov synthesis method for controller design. We start
with the conventional case, that is, when we have an exact mathematical description of the plant and then
describe its extension to the fuzzy case.
Consider the single-input, single-output system
Y;=F(x,u),
y:h(x),
(1)
where F(.)=(FI(.),F2(.) . . . . . Fn(.)) x with the Fi(.)'s being continuous functions, u E R and y E R are the
input and output of the system, respectively, and x---(Xl,X2 .... ,xn) T E R n is the state vector of the system.
The control objective is to stabilize the system around some working point xo (without loss of generality we
may assume xo = 0). More specifically: Design a feedback control u(x) so that 0 will be a stable equilibrium
point of (1). Alternative definitions of stability, (e.g., asymptotic stability, exponential stability) may be used.
One way of achieving this goal is to choose a Lyapunov function candidate V(x) and then determine the
conditions on u (note that V depends on x and therefore on u) necessary to make it a Lyapunov function.
In this paper, we refer to a continuously differentiable function V(x) as a Lyapunov function if the following
requirements are met:
A1.
V(0) : 0,
V(x)>O,
n
A3.
l ? = ~i=, ~x/:~i<0,
~V
xeN{0},
where N { 0 ) E R n is some neighborhood of 0 excluding the origin 0 itself, and Xi (i = 1,2 ..... n) is given by
(1). If 0 is an equilibrium point of (1) and such V exists, then 0 is locally asymptotically stable [5].
We now extend the idea to a more general (and realistic) scenario: Assume that the exact model (1)
is unknown but we do have some partial (fuzzy) knowledge about the system. As before, we determine a
Lyapunov function candidate V, derive an expression for its derivative, and then obtain conditions so that
V would indeed be a Lyapunov function. In this case, however, because our knowledge about the system is
incomplete and vague (fuzzy), the conditions obtained result in a fuzzy controller u.
We can formulate the resulting conditions in the form of rules in one of two possible representations. The
first form is:
IF xl is (Iv) and/or x2 is (Iv)... and/or x, is (Iv) THEN u must be (Iv).

3. M. Maroaliot, G. Lanoholz/Fuzzy Sets and Systems 106 (1999) 49-59
51
where the (Iv) are linguistic values (e.g. large, small). The second possible form is
IF xl is (Iv) and/or x2 is ( l v ) . . . and/or Xn is (lv) THEN u must be f ( x l , x 2 . . . . . x , )
where f ( ) is a linear function.
These rules constitute the rule base for a Mamdani-type [9] or Takagi-Sugeno-Kang-type (TSK) [6] fuzzy
controller, respectively. We refer to the method of deriving the rules as the fuzzy Lyapunov synthesis method.
To illustrate our approach, we apply it in the following sections to the design of fuzzy controllers for two
well-known plants. Following that, we discuss some generalizations in the concluding section.
3. Designing Mamdani-type controllers
In this section we apply the fuzzy Lyapunov synthesis approach to the design of stabilizing and tracking
controllers for the inverted pendulum system. We begin with the system's mathematical model, which is well
known, but we do so for reference only. As will become apparent in the sequel, our basic assumption is that
we know very little about the plant.
The system is illustrated in Fig. 1. Let xj = 0 and x2 = 0, then the system's dynamic equations are [5]
:~1 =x2,
(2)
Yc2 = F ( x l , x 2 ) + G(xl,x2)u,
where
F(Xl,X2) =
9 sinxl - (mlx 2 cosxl sinxl )/(me + m)
l( 4 - (mcos2xl)/(mc + m))
G(xl,x2 ) =
(COS X 1 )/(mc + m)
l( 4 - (m cos2xl )/(mc + m))'
O=X
7-'/
/
mc
©
©
Fig. 1. Inverted pendulum system.

4. M. Margaliot, G. Langholz/Fuzzy Sets and Systems 106 (1999) 49-59
52
g = 9.8 m/s 2 is the acceleration due to gravity, mc is the mass of the cart, m is the mass of the pole, 2l is
the pole's length, and u is the applied force (control). In the simulations we chose: mc = 1 kg, m = 0.1 kg and
l=0.5m.
To apply the fuzzy Lyapunov synthesis method we assume from here on that the exact equations (2) are
unknown and that we have only the following partial knowledge about the plant:
1. The relevant state variables are xl = 0 and x 2 = 0.
2. x2 is proportional to u, that is, when u increases (decreases) :~2 increases (decreases).
Obviously we assume very little knowledge indeed.
3.1. Designing a stabilizing controller
Our objective is to design U(XI,X2) that will balance the inverted pendulum, namely, to find u so that
(0, 0) r would be a stable point of (2). We choose V(Xl,X2)= ~(XI1 +X 2) as Our Lyapunov function candidate.
2
It clearly satisfies conditions A1, A2 and we need only worry about A3. Hence, since
V = X l X l -}-x2x2 =XlX2q-x2x2,
(3)
then to satisfy A3, we must have
XIX2 -~ X2)f2 < 0,
(4)
in some neighborhood of (0, 0) T.
We can now derive sufficient conditions for (4) to hold: If xl and x2 have opposite signs, then xlx2 < 0
and (4) will hold if A2=0; i f x l and x2 are both positive, then (4) will hold i f A 2 < - - X l ; and i f x l and x2
are both negative, then (4) will hold if ~2 > - X l .
Using these observations and our knowledge that ~72 is proportional to u, we obtain the following fuzzy
rules for the stabilizing controller:
• IF Xl is positive and x2 is positive THEN u is negative big,
• IF Xl is negative and x2 is negative THEN u is positive big,
• IF Xl is positive and x2 is negative THEN u is zero,
• IF xl is negative and x2 is positive THEN u is zero.
It is interesting to note that the fuzzy partitions for xl, x2, and u follow elegantly from expression (3).
Because I?=xe(xl +d2), and since we require that 1;" be negative, it is natural to examine the signs o f x l and
x2, so the obvious fuzzy partition is {positive, negative}. The partition for :~2, namely {negative big, zero,
positive big} was obtained similarly when we plugged the linguistic values {positive, negative} for xl and
x2 in (4). To ensure that ~ 2 < - x l 0 ? 2 > - X l ) is satisfied even though we do not know x l ' s exact magnitude, only that it is positive (negative), we must set A2 to negative big (positive big). Obviously, it is also
possible to start with a given, pre-defined, partition for the variables (e.g., Xl E {negative, zero, positive})
and then plug each linguistic value in the expression for l;" to find the rules. This is the approach we take
in Section 4. Nevertheless, regardless of what comes first, we see that fuzzy Lyapunov synthesis transforms
classical Lyapunov synthesis from the world of exact mathematical quantities to the world of computing with
words [ 10].
Following [8], we characterize the linguistic variables positive, negative, negative big, zero and positive big
by the membership functions

5. 53
M. Margaliot, G. Langholz/Fuzzy Sets and Systems 106 (1999) 49-59
25
1
0.8
20
0.6
:~
ea
8,
15
0.4
~
0.2
0
-0.2
~'- 10
-0.4 -o.8 .
.
.
.
.
.
.
-0.8 -
i
2
4
6
8
10
-0.15
-0.1
-0.05
Fig. 2. The pendulum's angle xl(t) for five initial conditions
(Xl(O),O).
]~ positive(X) =
/Jnegative(X) =
0
0.05
O. q
0,15
x 1 (rad)
t
Fig. 3. The pendulum's behavior in the phase plane for initial
condition xl(0) = 0.0698rat (= 4°), x2(0) = 1 rad/s.
1
1 + e x p ( - 30x)'
1
1 + exp(+ 30x)'
(5)
,/J negative big(U) = e x p ( - (u + 5)2),
]A zero(U) ---~ e x p ( - u 2),
]2positive big(U)= e x p ( - ( u -
5) 2)
and using the center of gravity defuzzifier and the product inference engine, we obtain the following stabilizing
controller:
U = - - 5 f l (Xl,X2) -I- 5f2(Xl ,X2),
where
fl
f2 =
positive 1)~ positive(X2)
(X
#positive(Xl )~posifive(X2 ) + ,Upositive(Xl)]~ negative(X2) + ~ negative(Xl)J2positive(X2) + ~negative(XI)# negative(X2)'
~negative(XI )/'1negative(X2)
#positive(Xl )~positive(X2) "[- ]Apositive(XI )]-/negative(X2) + ~negative(X1 ),/./positive(X2) +
,/-/negative(Xl)#negative(X2)"
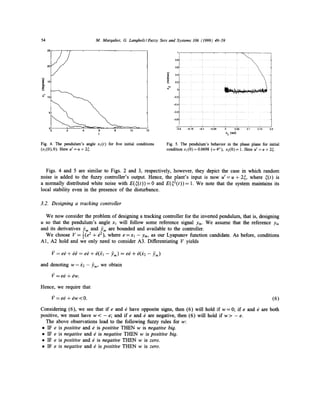
Figs. 2-5 display the simulation results of the closed-loop system. Fig. 2 shows the pendulum's angle Xl
as a function of time for the following five initial conditions: (Xl (0),x2(0)) = (4 °, 0), (9 °, 0), ( 12 °, 0), ( 17 °, 0),
(20 °, 0). We note that for small initial angles the controller drives the pendulum to the uptight position Xl = 0.
This indicates that local stability of the closed-loop system was indeed obtained.
Fig. 3 shows the pendulum's behavior in the phase plane for the initial condition X l ( 0 ) = 0.0698 rad ( = 4°),
x2(0) = 1 rad/s. Note that the angular speed x2 is first decreased till it is approximately zero and then the pole
moves slowly to the uptight position Xl = 0. This is in accordance with (3): since l? = x z ( x l +x2), then l? = 0
on the line x2 = 0.

6. M. Margaliot, G. LangholzlFuzzy Sets and Systems 106 (1999) 49-59
54
25
0.sf ~"
0.4
..........
i
; ........
i
.... i.......... !......
.........
......
o.2 . . . . . . . .......... i
0
2
4
6
8
10
t
Fig. 4. The p e n d u l u m ' s angle xl(t) for five initial conditions
(Xl(0),0). Here u / = u + 2 ~ .
-4
-o.;~
-o.,
i....... i
i
.......
-
. . . . . . . . .
.... i
-o.o~
;
o.o,
o.,
o.,~
0.2
x 1 (rad)
Fig. 5. The pendulttm's behavior in the phase plane for initial
condition xl (0) = 0.0698 ( = 4 °), x2(0) = 1. Here u ~ = u + 24.
Figs. 4 and 5 are similar to Figs. 2 and 3, respectively, however, they depict the case in which random
noise is added to the fuzzy controller's output. Hence, the plant's input is now u t - - u + 2¢, where ¢(t) is
a normally distributed white noise with E(¢(t))= 0 and E(~2(t))= 1. We note that the system maintains its
local stability even in the presence o f the disturbance.
3.2. Designing a tracking controller
We now consider the problem o f designing a tracking controller for the inverted pendulum, that is, designing
u so that the pendulum's angle Xl will follow some reference signal Ym. We assume that the reference Ym
and its derivatives )~m and Ym are bounded and available to the controller.
We choose V = l(e2 + ~2), where e =Xl - Ym, as our Lyapunov function candidate. As before, conditions
A1, A2 hold and we only need to consider A3. Differentiating V yields
12 = ek + ~ = ek + e ( x 1 - - J)m ) = eO + e ( x 2 -- J)m )
and denoting w = 3f 2 - J)m' we obtain
I? = e~ + kw.
Hence, we require that
V =ed + ~ w < 0 .
(6)
Considering (6), we see that if e and ~ have opposite signs, then (6) will hold if w = 0; if e and ~ are both
positive, we must have w < - e; and if e and ~ are negative, then (6) will hold if w > - e.
The above observations lead to the following fuzzy rules for w:
• IF e is positive and e is positive THEN w is negative big.
• IF e is negative and ~ is negative THEN w is positive big.
• IF e is positive and ~ is negative THEN w is zero.
• IF e is negative and ~ is positive THEN w is zero.

7. M. Margaliot, G. Lanohoh/Fuzzy Sets and Systems 106 (1999) 49-59
•
0,15
55
0.15,
0.1
0.051-'/
,i
i
J
',1
q
~
Ll
7
~I
q
0,05
1,4
-0.1
30
-0.15' 0
-0.(1
-o.lF
~.'/
-0.150
5
I,,'/
10
~ ~/
15
t
LJl
20
25
Fig. 6. The pendulum's angle xfft) (solid line) and the reference signal ym(t)= 7r/30 sin(t) (dashed line) for initial condition
(--n/60, 0).
=
5
1'0
1r5
t
2 l0
'
25
'
30
Fig. 7. The pendulum's angle xl(t) (solid line) and the reference signal ym = n/30sin(t) (dashed line) for initial condition
(-n/60,0). Here u t = u + 2~.
Using the membership functions (5), the center of gravity defuzzifier, and the product inference engine we
obtain the following:
w = - 5fl(e,6) + 5f2(e, 6),
(7)
where
fj =
,t/positive(e)//positive(e)
//positive(e)k/positive(e) -+-//positive(e)12negative(~') "+" ]-/negative(e)/-/positive(e) q-//negative(e)[/negative(e)'
/2negative (e)//negative ( e )
f2 = [/positive(e)/-/positive(e) q- ]-/positive(e)12negative(e) -~- ]-/negative(e)/-/positive(e) q-//negative(e)[/negative(e)"
Now, to obtain the tracking controller, we combine w = ~2 to u; hence
u = w + Pro-
tim with our knowledge that
X2
is proportional
(8)
Fig. 6 shows the simulation results for the closed-loop system given by (2) and (8). The reference signal is
Ym = (re/30)sin(t) and the initial condition is x l ( 0 ) = -rr/60, x2(0)= 0. Fig. 7 shows the simulation results
for the same conditions but with u t = u + 2¢, where ¢(t) is the normally distributed white noise considered
in Section 3.1. We note that adequate tracking is achieved in both cases.
As a final remark, note that we can ignore J)m altogether and set
u=w.
(9)
This yields the tracking controller suggested in [8]. However, numerical calculation of the tracking error
f03° e2(t)dt, yields 0.0105 when using (8) and 0.0125 when using (9). Hence, fuzzy Lyapunov synthesis
leads not only to a systematic design but also to extra insight that leads to a better controller.
Up to this point the rules necessary to make 17 negative were stated in the form leading to Mamdani-type
fuzzy controllers. In the following section we use our fuzzy Lyapunov synthesis method to design a TSK-type
fuzzy controller.

8. 56
M. Margaliot, G. LanoholzlFuzzy Sets and Systems 106 (1999) 49-59
q(t)
low
normal
high
1
0.8
0.6
f
0.4
0.2
,
v(z)u
/
Xs
X
Fig. 8. Water tank system.
Fig. 9. The operating conditions.
4. Designing TSK-type controller
In this section we use fuzzy Lyapunov synthesis to design a TSK-type fuzzy controller for regulating the
amount of water in a cylindrical water tank [1].
Illustrated in Fig. 8, the system's dynamical behavior is governed by the following differential equation:
:~ = q(t) - p(x)u,
(10)
where x is the amount of water in the tank, q(t) is the inflow to the tank (we assume that q(t) varies around
some nominal fixed flow qs), p(x)u is the outflow from the tank, where p(x)=av/2g(x/~zr 2) (a is a positive
constant, r is the tank's radius, and g = 9.8 m/s 2 is the acceleration due to gravity), and u, the control variable,
is the cross-sectional area of the drain opening.
The control objective is: Design u to regulate x(t) to a desired nominal amount Xs. We assume that (10)
is known but that p(x) is not explicitly known and the only knowledge we have about p(x) is
• p ( x ) is positive.
• The value Ps = p(Xs) is known.
Following [1], we assume that the fuzzy partition of the domain of x is already given, namely, the system
has three operating modes: x is low, x is normal, and x is high. Qualitatively, as depicted in Fig. 9, x is low
when x is much smaller than xs, x is high when x is much larger than xs, and x is normal when Ix -Xs[ is
small.
To determine the control rules in each of the three modes we apply the fuzzy Lyapunov synthesis method.
Consider the Lyapunov function candidate V = ½(x - xs)2 and differentiate it to yield
l? = (x - Xs)2 = (x - Xs)(q(t) - p(x)u).
(11)
Eq. (11) enables us to derive conditions for making /? negative in each of the operating modes: If x is low,
then ( x - x s ) < 0 . Hence, to make /? negative, we require q ( t ) > p(x)u. But, we know that q(t) and p(x) are
non-negative, therefore, we set u = 0 . Next, if x is high, then ( x - x s ) > 0 . Hence, to make 17 negative, we
require q ( t ) < p(x)u and set u = Umax, where Umax is the maximal opening of the drain. Finally, we consider

9. M. Margaliot, G. LanoholzlFuzzy Sets and Systems 106 (1999) 49-59
1000
1(;00
90C
57
9OO
80C
!
!
.....
800
!.
.
.
.
.
.
.
.
i
7OC
700
600
60O
:~ 500
500
400
400
.
300
300
.
200
200
.................
100
. . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
i
.
i
!
IO0
~ .........
:
~. . . . . . . . . . . . . . . . . . . . . . . . . . . .
~
. . . . . . . . . . .
. . . . . . . .
:"
i
0
5
0
lo
l's
2o
2'5
I
ao
as
4'o
4's
O0
t
Fig. 10. The amount of water x(t) starting from x(0) = 0 for the
nominal inflow.
5
I
10
15
i
20
25
t
,
i
30
35
40
~5
Fig. 11. The amount of water x(t) starting from x(0) = 1000 for
the nominal inflow.
the case where x is normal. Since we are designing a TSK-type fuzzy controller, we substitute u = klx + k2
in (11 ) to obtain:
= (x - Xs)(q(t) - p ( x ) ( k l x + k2)) = (x - Xs)(q(t) - p(x)(kl(x - Xs) + klxs + k2))
= - p ( x ) k l ( x - x~) 2 + (x - Xs)(q(t) - p(x)(klxs + k2)).
(12)
The first term in (12) is non-positive for any kl > 0 . AS for the second term, (x - X s ) ( q ( t ) - p(x)(klxs + k 2 ) ) ,
since we cannot determine its sign, we can try to make it as small as possible. In particular, we would like
( q ( t ) - p(x)(klxs + k2)) to vanish for x = x s because then the second term behaves approximately as ( x - Xs) 2
in the vicinity o f xs and, therefore, vanishes quickly. To this end, we set k2 = q s / P s - k l X s because then, if
q(t) =q~ and p ( x ) = p ( x ~ ) = Ps (this is a logical assumption when x is normal) we obtain
(q(t)-p(x)(klXs+k2))=
(qs-Ps(klxs+q-L-klXs))
So, when x is normal, u = klx + k2 = kl ( x - Xs )+-qs/Ps with kl > 0. Note, however, that the drain opening is
always non-negative, hence kl must satisfy: kl ( 0 - x s ) + qs/p~ >>,O. Therefore,
0<k] ~< q-2-s.
(13)
psXs
To summarize, using fuzzy Lyapunov synthesis, we have obtained the following TSK-type control rules for
the water tank system:
• If x is low then u = 0.
• If x is normal then u = kl (x - Xs) + qs/Ps.
• If x is high then u = Umax.
And, using the center o f gravity defuzzifier and the product inference engine, we obtain
u=
#normal(X)(kl (x - Xs) + qs/Ps) + #high(X)Umax
]21ow(X ) ~-/2normal(X ) Jr-/2high(X)
(14)

10. M. Margaliot, G. LangholzlFuzzy Sets and Systems 106 (1999) 49-59
58
10430
zt
900
800
700
700
6OO
60O
50(]
500
400
400
300
300
200
,
I
100
0
i~_
i
[I
'~.
~'l~
I
I
tl
~rll
5
I
II
i11
10
r___~t
Ill
IIII,
I--I
I
I
Illll
15
20
I
l'l I-
--I
J
I
--I
--I
I
II
~J~ _ r , ~ t _ _ , ~
i
L
25
ii
Iii
30
i
i h i i
35
__,~_.
i /i i
40
i
i
i
45
2O0
,,- ,,i
i
I1
ii
100
O'
_
,,,,~ 1. . .I . t ,~ _
i1
,,
Ii
,,
ii
ii
II
_
III
. . . . . . . . . . . . .
', '--' i'~ ,~",
'' ,, I', , ] !,,. . , . h. . ., , ~., , ,.' . . ' , . , l ' ~ !, ' ,
5
10
15
20
25
30
35
40
I
,,
ql I
1I
,
, ',
45
t
t
Fig. 12. The amount of water x(t) (solid line) starting from
x(0) = 0 for a random inflow q(t) (dashed line).
Fig. 13. The amount of water x(t) (solid line) starting from
x(0) = 1000 for a random inflow q(t) (dashed line).
We simulated the closed-loop system given by (1 O) and (14) using the following parameters: xs = 700, qs =
100, a - 1, r = 1, Umax= 5. For the controller, we used the membership functions (qualitatively depicted in
Fig. 9):
1
/ttow(X)- 1 + e 0-1(x-600)'
gnormal(X) = e -((x-700)/100)2,
1
[thigh(X) 1 + e -0l(x-800)
=
and the parameter kl = 2 × 10 -4. Note that from the definition of p(x) we obtain Ps = p ( x s ) = 66.085 and
qs/psXs=2.2 × 10 -3 so (13) is satisfied.
Figs. 10-13 depict the simulation results. Figs. I0 and 11 illustrate the system's behavior under the nominal
inflow q(t)=qs and initial conditions x ( 0 ) = 0 and x ( 0 ) = 1000, respectively. Figs. 12 and 13 illustrate the
system's behavior when q(t) varies randomly between 0, qs, and 2qs. Note that this causes x(t) to vary around
the desired nominal amount Xs.
5. Conclusions
In this paper, we presented a novel approach for determining the rule base of a fuzzy controller. Starting
with minimal knowledge concerning the plant's behavior, we choose a Lyapunov function candidate V and
determine conditions so that V will indeed be a Lyapunov function. These conditions provide us the rule base
of the fuzzy controller.
Our proposed fuzzy Lyapunov synthesis approach combines the best of two worlds. On the one hand, the
plant is model-free in the sense that only minimal fuzzy knowledge is available. On the other hand, it follows
the classical Lyapunov synthesis method. This combination provides us with a solid analytical basis from
which the rules are obtained and justified. Furthermore, the fuzzy Lyapunov synthesis method can certainly
contribute to the investigation of additional problems in the field of fuzzy control. We discuss three such
problems in the following paragraphs.
First, in the context of the control strategy used by human operators, it is interesting to quote [4, pp. 399]:
"The control behavior (of a human pilot) can be related to the total energy of the aircraft. For example,
if the pilot realizes that the aircraft flies too low and too slow, he or she will increase thrust in order to
increase the energy of the aircraft". I f human operators indeed develop a notion of the plant's energy and

11. M. Margaliot, G. Langholz/Fuzzy Sets and Systems 106 (1999) 49-59
59
use it to derive their control strategy, then they are in fact performing fuzzy Lyapunov synthesis. Thus, fuzzy
Lyapunov synthesis might aid in the understanding and extraction o f human control skills.
Another important issue pertains to the potential application o f our approach to the analytical study o f
the robustness o f the derived fuzzy controllers, that is usually demonstrated viz. simulations. Reconsidering
the examples, we note that only minimal, and therefore very general, information regarding the plants was
employed. This might suggest that the resulting rule base is applicable even when the structure or parameters
o f the plant vary, as long as the general fuzzy knowledge assumed remains valid.
Last, but not least, is the issue o f closed-loop stability. Since the obtained rule base is designed relative to
a Lyapunov function, the fuzzy Lyapunov synthesis approach can also assist in the stability analysis o f the
closed-loop system. For example, consider the following question: Given a plant, what is the minimal number
o f rules that a stabilizing fuzzy controller must include? We have shown [3], using the fuzzy Lyapunov
synthesis approach, that for linear time-invariant plants o f arbitrary order, four Mamdani-type fuzzy rules
will always suffice to guarantee local asymptotic stability.
References
[1] B. Kuipers, K. Astrom. The composition of heterogeneous control laws, in: A. Kandel, G. Langholz (Eds.), Fuzzy Control Systems,
CRC Press, 1994, Boca Raton, pp. 243-261.
[2] C.C. Lee, Fuzzy logic in control systems: fuzzy logic controller, parts I and II, IEEE Trans. System Man Cybernet. 20(2) (1990)
404-435.
[3] M. Margaliot, G. Langholz, Fuzzy Lyapunov synthesis - theoretical and practical considerations, IEEE Trans. System Man Cybernet.,
submitted.
[4] G. Schram, H.B. Verbruggen, A fuzzy control approach, in: J.F. Magni, S. Benani, J. Terlouw (Eds.), Robust Flight Control,
Springer, Berlin, 1997, pp. 397-416.
[5] J.J.E. Slotine, W. Li, Applied Nonlinear Control, Prentice-Hall, Englewood Cliffs, NJ, 1991.
[6] T. Takagi, M. Sugeno, Fuzzy identification of systems and its applications to modeling, and control, IEEE Trans. System Man
Cybemet. 15(1) (1985) 116-132.
[7] L.X. Wang, Adaptive Fuzzy Systems and Control, Prentice-Hall, Englewood Cliffs, NJ, 1994.
[8] L.X. Wang, A Course in Fuzzy Systems and Control, Prentice-Hall, Englewood Cliffs, NJ, 1997.
[9] R. Yager, D.P. Filev, Essentials of Fuzzy Modeling and Control, Wiley, New York, 1994.
[10] L.A. Zadeh, Fuzzy logic = computing with words, IEEE Trans. Fuzzy Systems 4(2) (1996) 103-111.