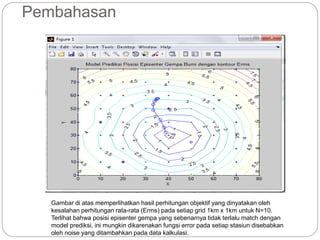
Dokumen ini membahas penentuan episenter gempa bumi menggunakan pemodelan inversi non-linear dengan metode grid search dan random search di MATLAB. Simulasi menunjukkan bahwa posisi episenter yang dihasilkan tidak selalu cocok dengan model prediksi karena adanya noise dalam data. Meskipun demikian, pendekatan global ini berguna untuk menghindari terjebak dalam minimum lokal saat pencarian solusi.

1. PENENTUAN EPISENTER GEMPA BUMI
DENGAN PEMODELAN INVERSI NON-
LINEAR(METODE PENDEKATAN
GLOBAL(METODE GRID SEARCH DAN
RANDOM SEARCH)) MENGGUNAKAN
MATLAB
Fisika Komputasi

2. Pendahuluan
Di pusat gempa bumi terdapat
tempat2 yang terakumulasi energi
Untuk menentukan posisi episenter
gempa bumi maka digunakan data
sintetik
Asalnya dari
Metode Grid
Search dan
Random Search
Data diproses dengan Matlab
Memberikan solusi inversi non linear
Plot bentuk kurva
dan kontur fungsi
objektif yg tersebar
secara random

3. Kajian Pustaka
Formulasi Linear dan Hubungan data dengan Parameter Model
Data: d = [di] ; i = 1, 2, 3, …N
d = (d1, d2, d3, …, dN)
Model: m = [mj] ; j = 1, 2, 3, …M
m = (m1, m2, m3, …, mM)
Hubungan antara data dg parameter model:
d = G m
G adalah matriks kernel
Contoh pada simulasi. Nilai d=Gm , nilai d = ti-gm
Rumus gm yang dipakai pada matlab adalah
gm=to+(1/vp)*(sqrt((x-M(1)).^2+(y-M(2)).^2));

4. Penambahan pengaruh error dari noise dengan
Metode Least-Square
adalah dengan meminimumkan jarak antara Tical (hasil perhitungan)
dengan Tiobs (hasil pengamatan).
Contoh pada simulasi. Oleh stasiun pertama:
t_cal1=to+(1/vp)*sqrt((x(1)-X).^2+(y(1)-Y).^2);
Error1=(t_cal1-ti(1)).^2;
Dalam bentuk diskrit, persamaan bisa dinyatakan sebagai
Hal ini terjadi karena waktu tempuh t tidak berbanding lurus dengan
parameter model v, melainkan berbanding terbalik. Hubungan ini
dinamakan non-linear terhadap v. Namun demikian, jika kita
mendefinisikan parameter model c = 1/v, dimana c adalah slowness
gelombang seismik.
Jika dalam garis regresi dinyatakan sebagai y = a0 + a1x maka data
memenuhi relasi yi = a0 + a1xi + ei, dimana ei disebut error

5. Pendekatan Global(Metode Grid Search dan Random
Search) sebagai Solusi Inversi Non Linear
Metode Grid Search Metode Random Search
secara berulang-ulang
mengevaluasi nilai fungsi pada
nilai-nilai variabel bebas tertentu
(selected values) secara acak
Jika banyaknya sampel yang
dicoba mencukupi, maka kondisi
optimumnya akan teramati. Dengan
demikian, metode ini menjadi
TIDAK EFISIEN!!. Pendekatan ini
pada umumnya akan menghasilkan
titik optimum global (bukan
optimum lokal). Oleh karena itu,
metode ini sangat cocok sekali
dengan tujuan dari makalah ini
karena simulasinya
menggunakan pendekatan
secara global.
metode yang dapat menghindari solusi untuk
tidak terjebak dalam minimum lokal dan sering
digunakan dalam relokasi hiposenter.
Kelemahannya pada waktu perhitungan yang
lama. Hal ini disebabkan pengujian solusi yang
banyak dalam ruang model. Alogritma ini
masih memiliki kekurangan, masih besar
kemungkinan untuk terjebak di minimum lokal.
Oleh karena itu, dipilihlah pendekatan
secara globalnya karena jika menggunakan
lokal maka akan menjadi invalid.

6. Flowchart
Input data to,vp,ti,xo,yo
for n=1:10
Untuk rumus penentuan episenternya:
gm=to+(1/vp)*(sqrt((x-M(1)).^2+(y-M(2)).^2));
dgm_dx=(1/vp)*(-(x-M(1)))./(sqrt((x-M(1)).^2+(y-
M(2)).^2));
dgm_dy=(1/vp)*(-(x-M(2)))./(sqrt((x-M(1)).^2+(y-
M(2)).^2));
J=[dgm_dx dgm_dy];
Mo=M;
M=Mo+inv(J'*J)*J'*(ti-gm)
M1=[M1 M];
Mn=M1';
Untuk error erms nya:
t_cal1=to+(1/vp)*sqrt((x(1)-X).^2+(y(1)-Y).^2);
Error1=(t_cal1-ti(1)).^2;
t_cal2=to+(1/vp)*sqrt((x(2)-X).^2+(y(2)-Y).^2);
Error2=(t_cal2-ti(2)).^2;
t_cal3=to+(1/vp)*sqrt((x(3)-X).^2+(y(3)-Y).^2);
Error3=(t_cal3-ti(3)).^2;
t_cal4=to+(1/vp)*sqrt((x(4)-X).^2+(y(4)-Y).^2);
Error4=(t_cal4-ti(4)).^2;
Plot posisi episenter dari stasiun 1 sampai 4:
plot(X,Y,'.')
xlabel('Longitude');
ylabel('Latitude');
plot(Mn(:,1),Mn(:,2),'o')
hold on
plot(Mn(:,1),Mn(:,2))
End
Start

7. Skip program
%Penentuan Episenter Gempa Bumi secara Sederhana
%Inversi Non Linear Metode Pendekatan Global(Grid Search dan Random
Search)
clear all
clc
to=0; % origin time
vp=4; % kecepatan gelombang gempa
ti=[7.1;1.8;5;7.9]; % waktu tempuh masing2 stasiun
x=[20;50;40;10];
y=[10;25;50;40]; % posisi stasiun
h=length(x);
plot(x,y,'h')
hold on
M=[40;30]; % posisi tebakan awal
[X,Y]=meshgrid(0:10:80,0:10:80);
plot(X,Y,'.')
xlabel(‘X');
ylabel(‘Y');

8. M1=[];
for n=1:10
gm=to+(1/vp)*(sqrt((x-M(1)).^2+(y-M(2)).^2));
dgm_dx=(1/vp)*(-(x-M(1)))./(sqrt((x-
M(1)).^2+(y-M(2)).^2));
dgm_dy=(1/vp)*(-(x-M(2)))./(sqrt((x-
M(1)).^2+(y-M(2)).^2));
J=[dgm_dx dgm_dy];
Mo=M;
M=Mo+inv(J'*J)*J'*(ti-gm)
M1=[M1 M];
Mn=M1';
end;
plot(Mn(:,1),Mn(:,2),'o')
hold on
plot(Mn(:,1),Mn(:,2))

9. % oleh stasiun pertama
t_cal1=to+(1/vp)*sqrt((x(1)-X).^2+(y(1)-Y).^2);
Error1=(t_cal1-ti(1)).^2;
% oleh stasiun kedua
t_cal2=to+(1/vp)*sqrt((x(2)-X).^2+(y(2)-Y).^2);
Error2=(t_cal2-ti(2)).^2;
% oleh stasiun ketiga
t_cal3=to+(1/vp)*sqrt((x(3)-X).^2+(y(3)-Y).^2);
Error3=(t_cal3-ti(3)).^2;
% oleh stasiun keempat
t_cal4=to+(1/vp)*sqrt((x(4)-X).^2+(y(4)-Y).^2);
Error4=(t_cal4-ti(4)).^2;
Erms=sqrt((1/n)*(Error1+Error2+Error3+Error4));
[cs,h]=contour(X,Y,Erms,[0:0.5:15])
clabel(cs,h)

10. Pembahasan
Gambar di atas memperlihatkan hasil perhitungan objektif yang dinyatakan oleh
kesalahan perhitungan rata-rata (Erms) pada setiap grid 1km x 1km untuk N=10.
Terlihat bahwa posisi episenter gempa yang sebenarnya tidak terlalu match dengan
model prediksi, ini mungkin dikarenakan fungsi error pada setiap stasiun disebabkan
oleh noise yang ditambahkan pada data kalkulasi.

11. Simpulan
Berdasarkan analisis yang telah dilakukan diketahui bahwa untuk
mengetahui cara menentukan episenter gempa bumi dari sumber gempa
secara sederhana dengan menggunakan Pemodelan Inversi Non
Linear,dimana pada pemodelan itu dilakukan pendekatan secara global
dengan metode grid search dan random search. Sedangkan, pada simulasi
diketahui bahwa plot posisi episenter gempa bumi tidak terlalu match
dengan model prediksi. Faktor yang mempengaruhi hal tersebut adalah
adanya penambahan error akibat noise saat pengambilan data.