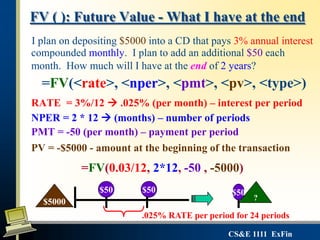
The document discusses financial functions in Excel for calculating values related to loans, savings, and investments with compound interest. It defines the key functions - PV, FV, PMT, RATE, and NPER - which use the variables of present value, future value, payment, interest rate, and number of periods. The functions allow calculation of loan payments, savings growth, and other financial transactions over time. The document also explains the importance of specifying the correct compounding periods and using the "type" argument appropriately in the functions.

1. CS&E 1111 ExFin
Microsoft Excel Financial Functions
Objectives:
Understanding and using
Financial Functions
•the time value of money
•PV, FV, Rate, NPER, PMT
•problem solving

2. CS&E 1111 ExFin
Simple Interest vs. Compound
Interest
Simple interest always calculates interest based on
the original amount.
So $1000 at 4% per year for 2 years
l Year 1: $1000 * 4%  $40 in interest for the
first year.
l Year 2: $1000 * 4%  $40 in interest for the
second year.
So after 2 years you would have
$1000 * 4% *2  $80 interest
For a total of $1080

3. CS&E 1111 ExFin
Compound interest - always calculate interest
based on “latest amount”
–Year 1: $1000 at 4%/yr for 1 year is $40
– Year 2: $1040* 4% =$41.60
Simple Interest vs. Compound Interest
T otal Inter est
$79.00
$80.00
$81.00
$82.00
Simple Interest Compound Interest
Si mpl e Inter est Compound Inter est
so now after 2 years you have $1081.60

4. CS&E 1111 ExFin
What if we compound our interest quarterly instead of
yearly? $1000 at 4% per year compounded quarterly for
one year is actually 4 separate calculations – Each
quarter updating the principa1 and using the rate 1% per
quarter.
Compounding Interest Quarterly
Principal Interest
1st quarter $1000.00*1% = $10.00
2nd quarter $1010.00*1% = $10.10
3rd quarter $1020.10*1% = $10.201
4th quarter $1030.301*1% ≈ $10.30
Total interest for year 1 ≈ $40.60 vs. $40 for simple interest

5. CS&E 1111 ExFin
l Functions that can be used to calculate
values based on compounded interest
- Taking a loan
- Investing in a savings account
l The basic financial functions use these 5
basic variables :
PV, FV, RATE, PMT, NPER
l Other functions are also available: NPV,
PPMT, IPMT
Financial Functions

6. CS&E 1111 ExFin
l PV: present value, what you get/pay at
the beginning of the financial transaction
l FV: future value, what you are going to
get OR what you will have to pay at the
end of the financial transaction
l PMT: payment made each period. It
remains constant over life of annuity
l RATE: interest rate per period
l NPER: number of payment periods
The Basics

7. CS&E 1111 ExFin
$100 Loan for 2 Years Compounded
Quarterly at 8% per year
Beginning
PV $100
End
FV $0
Interest RATE per compounding period (8% per
yr/4 qtr per year) for NPER periods (2yrs * 4
Qtr/yr) with Payments PMT($13.65) - In/Out at
Equal Intervals
2% RATE for each of 8 Quarters
$13.65 PMT for each of 8 Quarters

8. CS&E 1111 ExFin
How much money would I have to set aside now to
have a $5000 down payment on a car when I graduate
in 2 years? I plan to put the money in a CD that pays
3% annual interest compounded yearly.
=PV(<rate>, <nper>, <pmt>, <fv>, <type>)
RATE = 3% (per year) – interest per period
NPER = 2 (years) – number of periods
PMT = 0 (per year) – payment per period
FV = $5000 - amount at the end of the transaction
=PV(0.03, 2, 0,5000)
PV ( ): Present Value - What I have at the beginning
? 5000
$0 $0
3% RATE per period

9. CS&E 1111 ExFin
When using Financial Functions remember to..
l Use consistent units of time
l RATE per quarter, NPER number of quarters and
PMT payment per quarter.
l Use consistent signs
l outgoing cash: (- ), incoming cash: (+ )
l For arguments that are zero at least a comma
must be put into the function to maintain the
argument order, unless no other non-zero
arguments follow – then it many be deleted.
=PV(0.03, 2, 0, 5000,0) same as =PV(0.03, 2, , 5000)

10. CS&E 1111 ExFin
I plan on depositing $5000 into a CD that pays 3% annual interest
compounded monthly. I plan to add an additional $50 each
month. How much will I have at the end of 2 years?
=FV(<rate>, <nper>, <pmt>, <pv>, <type>)
RATE = 3%/12  .025% (per month) – interest per period
NPER = 2 * 12  (months) – number of periods
PMT = -50 (per month) – payment per period
PV = -$5000 - amount at the beginning of the transaction
FV ( ): Future Value - What I have at the end
$5000 ?
$50 $50
.025% RATE per period for 24 periods
$50
=FV(0.03/12, 2*12, -50 , -5000)

11. CS&E 1111 ExFin
PMT( ): Returns the periodic payment
I have been offered a 5 year car loan of $15,000 at 9% annual
interest rate compounded monthly. What is the monthly payment
needed to completely pay off the loan at the end of the 5 years?
=PMT(<rate>, <nper>, <pv>, <fv>, <type>)
=PMT(B3/B5, B4*B5, B1, B2)
:
Will your payment be a positive or negative value?
1
2
3
4
5
6
A B
Original Loan Value 15,000
$
Ending Loan Value -
$
Yearly Interest Rate 9%
Number of Years 5
Compounding Periods per Year 12
Monthly Payment ($311.38)

12. CS&E 1111 ExFin
What is the annual rate
of interest of this loan –
assuming it is
compounded monthly.
Rate( ): Returns Rate per Period
$18,999 for
a new Chevy Cruze
$2000 down and
$350/month
For 5 years
=RATE(<nper>, <pmt>, <pv>, <fv>, <type>)
=RATE(5*12, -350, 18999-2000) * 12 months per yr
Remember to get the correct compounding - calculate rate per
period (month)  then convert it to rate per year.

13. CS&E 1111 ExFin
NPER( ) : # Payment Periods
Write an Excel formula to determine how many
years will it take to save $12,000 if I put $10,000
into a savings account paying 4% annual interest
compounded quarterly.
=NPER(<rate>, <pmt>, <pv>, <fv>, <type>)
=NPER(4%/4, , -10000, 12000) /4 quarters per yr
Remember to get the correct compounding - calculate the
number of periods (quarterly) and then convert to years.

14. CS&E 1111 ExFin
The “type” argument:
Type If payments are made:
0 (default) At the end of the period
1 At the beginning of the period
Example:
l Type 0: You make a car payment to the bank at
the end of each month to pay down the principal
l Type 1: An annuity pays you a set amount each
month at the beginning of the month
Unless specifically mentioned assume type 0

15. CS&E 1111 ExFin
The “type” argument:
I have been putting $100 per
quarter in the bank for the past
10 years in an effort to save
money for my child’s college
education. How much money is
currently in this account
assuming the bank has paid a
3% annual interest rate
compounded quarterly?
Make Payments at the End
of Each Quarter:
=FV(.03/4, 4*10, -100,0,0)
Make Payments at the
Beginning of Each Quarter:
=FV(.03/4, 4*10, -100,0,1)
1
2
3
A B
Payment at
Beginning of
the Month
Payment at
End of the
Month
$4,679.48 $4,644.65
Value in 10 Years

16. CS&E 1111 ExFin
Another problem……
Write an Excel formula in cell D4 that can be copied down the
column to calculate the monthly payment for each of the
mortgages listed. The annual interest rate is 4% compounded
monthly. Note: A balloon payment is an amount due at the
end of the loan.
=PMT(<rate>, <nper>, <pv>, <fv>, <type>)
=PMT(B$1/12, B4*12, A4, -C4)
1
2
3
4
5
6
7
A B C D
Interest Rate 4%
Loan Amount # Years
Balloon
Payment
Monthly
Payment
100000 30 0 ($477.42)
100000 30 10000 ($463.01)
100000 15 0 ($739.69)
100000 15 10000 ($699.05)

17. CS&E 1111 ExFin
A Summary of Financial Functions
l Financial Function can be used to calculate
financial transactions with compound interest.
l PV, FV, PMT, NPER, RATE are all dependent
on the values of the other four
l Use positive values for cash flow back to you,
and negative values for cash flow from you to
a financial institution..
l Use correct compounding periods for your
values of NPER, PMT and RATE.
l Use the correct type argument