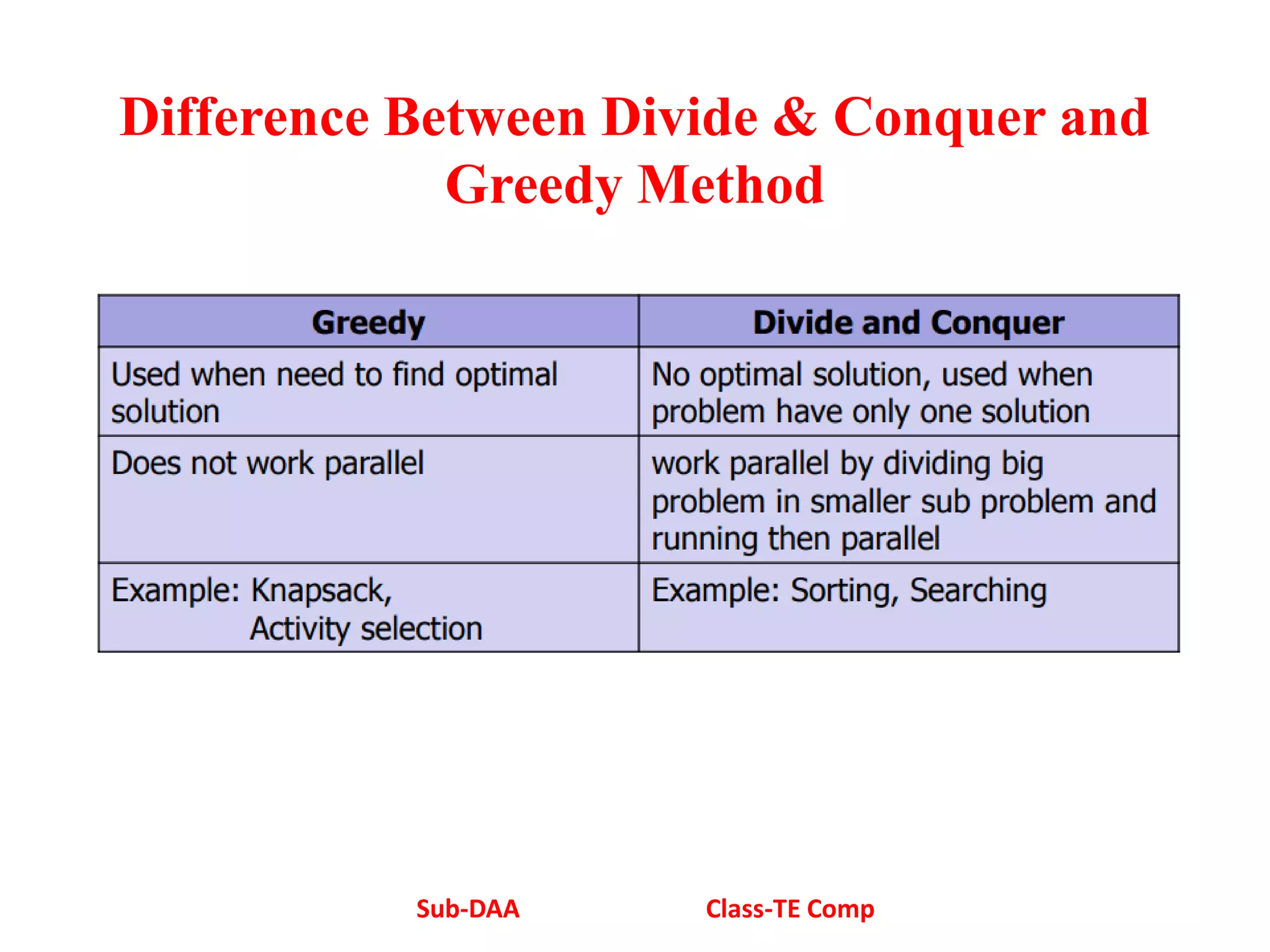
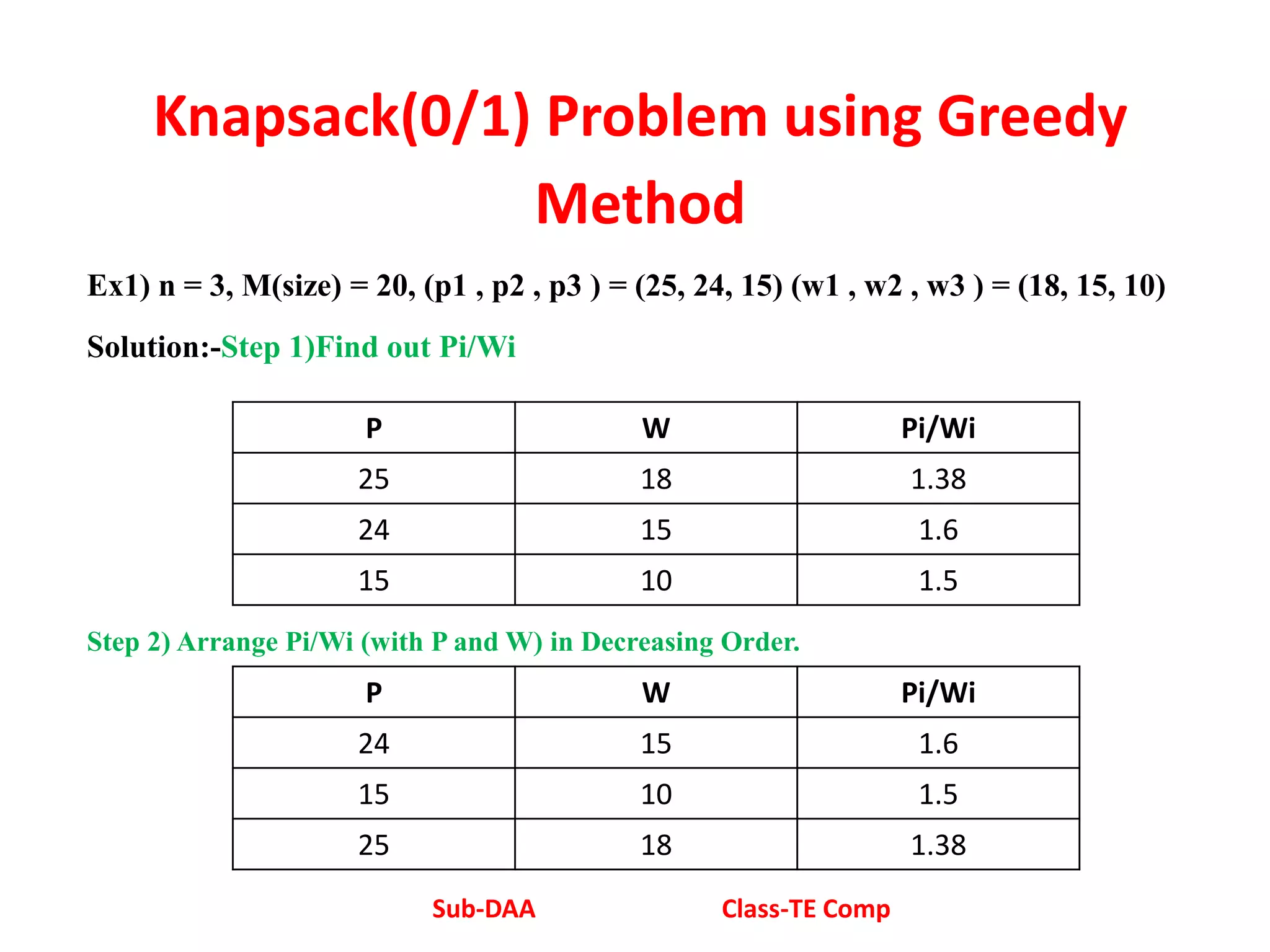
The document discusses greedy algorithms and their applications. Greedy algorithms make locally optimal choices at each step to arrive at a global solution. They are used to solve optimization problems by considering inputs in order based on a selection measure. Applications mentioned include knapsack problem, minimum spanning tree, job sequencing, Huffman coding, and shortest path. Specific details are provided on the knapsack problem and job sequencing problem algorithms.

1. Unit-III
Abstract
Algorithms
Sub-DAA Class-TE Comp

2. Greedy Method
• Greedy Principal: are
typically used to solve
optimization problem.
• Most of these problems have
n inputs and require us to
obtain a subset that satisfies
some constraints.
• Any subset that satisfies these
constraints is called a feasible
solution.
• We are required to find a
feasible solution that either
minimizes or maximizes a
given objective function
Sub-DAA Class-TE Comp

3. • Subset Paradigm : Devise an algorithm that works in stages
• Consider the inputs in an order based on some selection procedure
• Use some optimization measure for selection procedure
• At every stage, examine an input to see whether it leads to an
optimal solution
• If the inclusion of input into partial solution yields an infeasible
solution, discard the input; otherwise, add it to the partial solution
Applications of Greedy Method:
 Knapsack Problem
 Minimum Spanning Tree
 Job Sequencing Problem
 Huffman Code Generation
 Activity Selection Problem
 Shortest Path
Sub-DAA Class-TE Comp

4. Control Abstraction or Algorithm of
Greedy Method
Sub-DAA Class-TE Comp

5. Difference Between Divide & Conquer and
Greedy Method
Sub-DAA Class-TE Comp

6. Knapsack Problem
Sub-DAA Class-TE Comp
 The knapsack problem is a problem of optimization: Given a set of
items n, each with a weight w and profit p, determine the number of
each item to include in a knapsack such that the total weight is less
than or equal to a given knapsack limit M and the total Profit is
maximum.
 There are two types of Knapsack Problem.
 The 0-1 Knapsack Problem: same as integer knapsack except that
the values of xi 's are restricted to 0 or 1.
 The Fractional Knapsack Problem : same as integer knapsack
except that the values of xi 's are between 0 and 1.

7. Knapsack Problem Formula
Sub-DAA Class-TE Comp

8. Knapsack Problem Algorithm and
Time Complexity
Sub-DAA Class-TE Comp
Algorithm GreedyKnapsack (m, n)
// P[1 : n] and w[1 : n] contain the profits and
weights respectively of
// Objects ordered so that p[i] / w[i] > p[i + 1] /
w[i + 1].
// m is the knapsack size and x[1: n] is the
solution vector.
{
for i := 1 to n do x[i] := 0.0 // initialize x U := m;
for i := 1 to n do
{
if (w(i) > U) then break;
x [i] := 1.0; U := U – w[i];
}
if (i < n) then x[i] := U / w[i];
}
Running time:
The objects are to be sorted
into non-increasing order of
pi / wi ratio.
But if we disregard the time to
initially sort the objects, the
algorithm requires only O(n)
time

9. Sub-DAA Class-TE Comp
Knapsack(0/1) Problem using Greedy
Method
Ex1) n = 3, M(size) = 20, (p1 , p2 , p3 ) = (25, 24, 15) (w1 , w2 , w3 ) = (18, 15, 10)
Solution:-Step 1)Find out Pi/Wi
Step 2) Arrange Pi/Wi (with P and W) in Decreasing Order.
P W Pi/Wi
25 18 1.38
24 15 1.6
15 10 1.5
P W Pi/Wi
24 15 1.6
15 10 1.5
25 18 1.38

10. Sub-DAA Class-TE Comp
• Step 3) Insert Weight into bucket upto size M
15(w2)
M=20
5(w3)
15(w2)
Step 4) Solution
W1 W2 W3
0 1 ½ (10/2=5)
Step 5) Calculate Total Profit
=P1*0+ P2*1 +P3* ½
=25*0+24*1+15*1/2
=0+24+7.5
Total Profit= 31.5

11. Sub-DAA Class-TE Comp
Ex 2) n = 3, M(size) = 20, (p1 , p2 , p3 ) = (30, 21, 18) (w1 , w2 , w3 ) = (18, 15, 10)
Solution: Step-1) Arrange Pi/Wi (with P and W) in Decreasing Order.
W1 W2 W3
1/2 1/15 1
P W Pi/Wi
18 10 1.8
30 18 1.66
21 15 1.4
Step 2) Insert Weight into bucket
upto size M M=20
1
9
10
Step 3) Solution
Step 4) Find the total Profit
Total Profit= 18+21*1/15+15
=18+1.4+15=34.4

12. Sub-DAA Class-TE Comp
Ex1) n = 5, M(size) = 100,
(p1 , p2 , p3,p4,p5 ) = (10,20,30,40,50)
(w1 , w2 , w3 ,w4 ,w5 ) = (20,30,66,40,60)
Solution:=
Weight=40+60=100
Profit=0+0+0+40+50
=90

13. Sub-DAA Class-TE Comp
Job sequencing using Greedy Method
The problem is stated as below.
 There are n jobs to be processed on a
machine.
 Each job i has a deadline di≥ 0 and profit
pi≥0 .
 Pi is earned if the job is completed by its
deadline.
 The job is completed if it is processed on a
machine for unit time.
 Only one machine is available for
processing jobs.
 Only one job is processed at a time on the
machine.
 A feasible solution is a subset of jobs J such
that each job is completed by its deadline.
 An optimal solution is a feasible solution
with maximum profit value.
Job Sequencing Algorithm:
Algorithm GreedyJob (d, J, n)
// J is a set of jobs that can be
completed by their deadlines.
{
J := {1};
for i := 2 to n do
{
if (all jobs in J U {i} can be
completed by their dead lines) then J
:= J U {i};
}
}

14. Sub-DAA Class-TE Comp
Job sequencing using Greedy Method
Formula:-
For slot assign:-
=[ Alpha(a)-1, Alpha(a)]
Optimal Solution:-
i.e ∑pi 1≤ i≤ n

15. Job sequencing using Greedy Method Example
Ex 1) Solve following using JSD Method
Where n=5
Sub-DAA Class-TE Comp
JOBs J1 J2 J3 J4 J5
Profit 20 15 10 5 1
Deadline 2 2 1 3 3
Job Consider Slot Assign Solution Profit
J1 [2-1,2]=[1,2] J1 20
J2 [1,2] [0,1] J1,J2 20+15
J3 [1,2] [0,1] J1,J2 20+15
J4 [1,2] [0,1]
[2,3]
J1,J2,J4 20+15+5
J5 [1,2] [0,1]
[2,3]
J1,J2,J4 20+15+5=40
Solution:-Step-1) Arrange all Job in Descending Order
Step-2) Job Sequence Path :- 0…J2…..1…J1….2…J4….3
Profit:- 20+15+5=40

16. Ex2)N=4 (p1,p2,p3,p4)=(100,10,15,27)
(d1,d2,d3,d4)=(2,1,2,1)
Ex3) N=5 (p1,p2,p3,p4,p5)=(25,15,12,5,1)
(d1,d2,d3,d4,d5)=(3,2,1,3,3)
Sub-DAA Class-TE Comp

17. Minimum Spanning Tree
Sub-DAA Class-TE Comp
Minimum Spanning Trees (MST):
 A spanning tree for a connected graph is a tree whose vertex set is the same
as the vertex set of the given graph, and whose edge set is a subset of the
edge set of the given graph. i.e., any connected graph will have a spanning
tree.
 Weight of a spanning tree w (T) is the sum of weights of all edges in T. The
Minimum spanning tree (MST) is a spanning tree with the smallest possible
weight.

18. Sub-DAA Class-TE Comp
Prims Algorithm
How Prim's algorithm works
It falls under a class of algorithms called greedy algorithms that find the local
optimum in the hopes of finding a global optimum.
We start from one vertex and keep adding edges with the lowest weight until we
reach our goal.
The steps for implementing Prim's algorithm are as follows:
1.Initialize the minimum spanning tree with a vertex chosen at random.
2.Find all the edges that connect the tree to new vertices, find the minimum and
add it to the tree
3.Keep repeating step 2 until we get a minimum spanning tree

19. Sub-DAA Class-TE Comp
Kruskal's Algorithm
How Kruskal's algorithm works
It falls under a class of algorithms called greedy algorithms that find the local
optimum in the hopes of finding a global optimum.
We start from the edges with the lowest weight and keep adding edges until we
reach our goal.
The steps for implementing Kruskal's algorithm are as follows:
1.Sort all the edges from low weight to high
2.Take the edge with the lowest weight and add it to the spanning tree. If
adding the edge created a cycle, then reject this edge.
3.Keep adding edges until we reach all vertices.