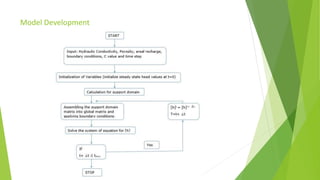
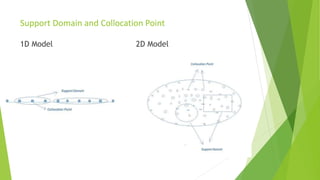
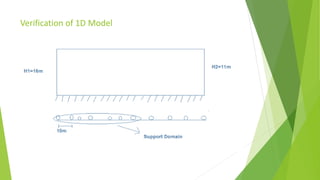
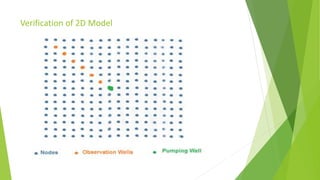
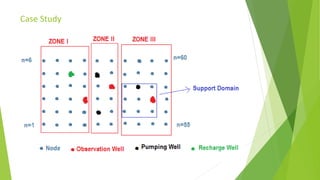
This document describes the development of a meshless point collocation method (PPCM) for simulating 1D and 2D groundwater flow. PPCM is a numerical technique that can establish algebraic equations over a problem domain without a predefined mesh, using scattered nodes. The document outlines the governing equations for 1D and 2D transient groundwater flow. It then describes how PPCM formulates these equations by defining a trial solution using shape functions and radial basis functions. The document verifies the 1D and 2D PPCM models against analytical and finite element method solutions. It also presents a case study application of the 2D PPCM model to a hypothetical confined aquifer with varying properties.

1. Meshless Point collocation Method For 1D and 2D
Groundwater Flow Simulation
By Under Supervision of
Ashvini Kumar Prof Anirban Dhar
10CE31005

2. Introduction
 Groundwater contamination and soil pollution have been recognized as
critical environment problems therefore flow of groundwater must be
analysed.
 Analysing flow of ground water through analytical method or numerical
methods like FEM and FDM or boundary element method is complex.
 Meshfree method is a powerful numerical technique to obtain more accurate
approximate solutions in a more convenient manner for complex systems.
 This method is used to establish algebraic equation for the whole problem
domain without the use of pre-defined mesh.
 Different from FDM and FEM, Mfree method use a set of scatted nodes in the
problem domain and boundaries of the domain.
 In present project, Mfree model is developed for groundwater flow problems
in 1D and 2D based on collocation techniques.

3. Literature Review
 Type of models use to study flow of groundwater can be classified in three
categories
 Sand Tank Models
 Analog Model
 Viscous Fluid Model
 Electrical Models
 Mathematical Models
 Analytical Models
 Numerical Models

4. Problem Description
In this project, a meshless method called as Polynomial Point collocation method
(PPCM) with radial basis function has been developed for the groundwater flow
simulation in porous media in one and two dimensions. The developed model has
been applied for computing head distribution in a hypothetical confined aquifer
having different boundary conditions and source, and sink terms. The developed
model is tested with analytical and FEM solutions available in literature and
found to be satisfactory.

5. Development of PPCM Equation for analysis of flow of
groundwater
 Governing equation of flow of groundwater

6. PPCM formulation for 1D transient Flow equation for
confined aquifer
 The transient of groundwater in homogeneous isotropic media in 1D can be
written as
Where, K is hydraulic conductivity (m/d) of the aquifer
Sy is specific yield
 To use Mfree method, the first step is to define the trial solution as
where, is unknown head
is the shape function at node I
n is the total number of nodes in the support domain
is given by
and
ℎ푖

7. PPCM formulation for 1D transient Flow equation for
confined aquifer
 For MQ-RBF, q=0.5, therefore can be written as
and therefore
and
Using earlier introduce equation, we get
Arranging previous equation, we get
(PPCM model for 1D flow of groundwater)

8. PPCM formulation for 2D transient flow equation for
confined aquifer
 The transient of groundwater in homogeneous isotropic media in 2D can be written as
 Again to use Mfree method, the first step is to define the trial solution as
where,
 Single and double derivatives of shape function w.r.t x and y can be written as
 Putting these equation in first equation and arranging the terms, we get
where, [K1] is global matrix of shape function
[K2] is global matrix of double derivative of shape function w.r.t. x
[K3] is global matrix of double derivative of shape function w.r.t y

9. Model Development

10. Support Domain and Collocation Point
1D Model 2D Model

11. Verification of 1D Model

12. Verification of 1D model

13. Verification of 2D Model

14. Verification of 2D Model
Node No. t=0.2 days t=1day
Analytical FEM % Error
(analytical
with FEM)
PPCM %Error
(Analytical with
PPCM)
FEM PPCM %Difference
FEM with
PPCM
29 97.013 96.993 0.02 97.0316 0.019 97.2316 97.2316 0.084
43 93.804 93.768 0.036 93.7606 0.046 94.0059 94.0059 0.047
57 90.095 90.051 0.044 90.0756 0.022 90.0245 90.0245 0.133
71 85.451 85.413 0.038 8 0.07 85.6105 85.6105 0.041
85 78.983 78.974 0.009 78.9544 0.024 78.8544 78.8544 0.272
99 67.953 67.762 0.191 67.8552 0.144 67.8212 67.8212 0.204

15. Verification of 2D Model

16. Case Study

17. Case Study
Properties ZONE I ZONE II ZONE III
Transmissivity Tx (m2/d) 500 400 250
Transmissivity Ty (m2/d) 300 250 200
Porosity 0.2 0.25 0.15

18. Case Study
Node No. FEM PPCM % Difference
21 98.2 98.149 0.0129
34 97.1 96.927 0.0445
51 95.25 95.313 0.0165

19. Case Study

20. Thank You All