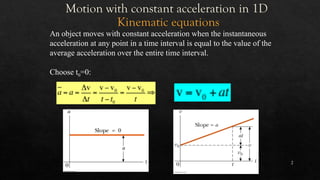
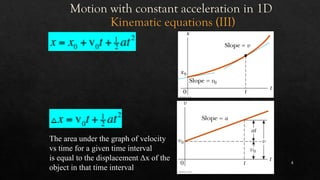
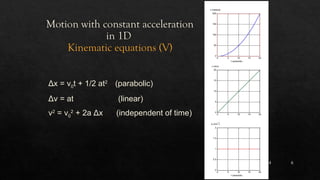
The document presents the principles of motion under constant acceleration, particularly in one-dimensional contexts, including kinematic equations and the effects of free fall. It emphasizes that objects accelerate uniformly under gravity, with practical examples illustrating concepts such as initial and final velocity, displacement, and the nature of free fall. Additionally, it discusses the implications of these principles through various thought experiments and calculations related to motion.

1. Motion under
constant
Acceleration
Edit by: Muhammad Faheem
Roll no /21CH057/
ENGINEERING
MECHANICS
Presentation Conduct By: Dr Fahad abro

2. 2
Motion with constant acceleration in 1D
Kinematic equations
An object moves with constant acceleration when the instantaneous
acceleration at any point in a time interval is equal to the value of the
average acceleration over the entire time interval.
Choose t0=0:

3. 08/11/2024 3
Motion with constant acceleration in 1D
Kinematic equations (II)
Because velocity changes uniformly with time, the average velocity
in the time interval is the arithmetic average of the initial and final
velocities:
(1)
(2)
Putting (1) and (2) together:

4. 08/11/2024 4
Motion with constant acceleration in 1D
Kinematic equations (III)
The area under the graph of velocity
vs time for a given time interval
is equal to the displacement Δx of the
object in that time interval

5. 08/11/2024 5
Motion with constant acceleration in 1D
Kinematic equations (IV)
Putting the following two formulas together another way:

6. 08/11/2024 6
Motion with constant acceleration
in 1D
Kinematic equations (V)
Δx = v0t + 1/2 at2
(parabolic)
Δv = at (linear)
v2
= v0
2
+ 2a Δx (independent of time) 0
5
10
15
20
0 5 10 15 20
v (m/s)
t (seconds)
0
50
100
150
200
0 5 10 15 20
x (meters)
t (seconds)
0
0.5
1
1.5
2
0 5 10 15 20
a (m/s
2
)
t (seconds)

7. 08/11/2024 7
Use of Kinematic Equations
 Shows velocity as a function of
acceleration and time
 Use when you don’t know or need the
displacement
 Gives displacement as a function of
velocity and time
 Use when you don’t know or need the
acceleration
 Gives displacement given time,
velocity & acceleration
 Use when you don’t know or need
the final velocity
 Gives velocity as a function of
acceleration and displacement
 Use when you don’t know or need
the time

8. Example for motion with a=const in 1D:
Free fall
08/11/2024 8
The Guinea and Feather tube
Earth’s gravity accelerates
objects equally, regardless
of their mass.
Experimental observations:

9. 08/11/2024 9
Free Fall Principles
 Objects moving under the influence of gravity only are in free fall
 Free fall does not depend on the object’s original motion
 Objects falling near earth’s surface due to gravity fall with constant
acceleration, indicated by g
 g = 9.80 m/s2
 g is always directed downward
 toward the center of the earth
 Ignoring air resistance and assuming g doesn’t vary with altitude over
short vertical distances, free fall is constantly accelerated motion

10. 08/11/2024 10
Summary: Constant Acceleration
Constant Acceleration:
x = x0 + v0xt + 1/2 at2
vx = v0x + at
vx
2
= v0x
2
+ 2a(x - x0)
Free Fall: (a = -g)
y = y0 + v0yt - 1/2 gt2
vy = v0y - gt
vy
2
= v0y
2
- 2g(y - y0)
x
y
up
down

11. 08/11/2024 11
A ball is thrown straight up in the air and returns to its initial position. For the
time the ball is in the air, which of the following statements is true?
1 - Both average acceleration and average velocity are zero.
2 - Average acceleration is zero but average velocity is not zero.
3 - Average velocity is zero but average acceleration is not zero.
4 - Neither average acceleration nor average velocity are zero.
Example 1
correct
Free fall: acceleration is constant (-g)
Initial position = final position: Δx=0
averaged vel = Δx/ Δt = 0

12. 08/11/2024 12
Free Fall dropping & throwing
 Drop
 Initial velocity is zero
 Acceleration is always g = -9.80 m/s2
 Throw Down
 Initial velocity is negative
 Acceleration is always g = -9.80 m/s2
 Throw Upward
 Initial velocity is positive
 Instantaneous velocity at maximum height is 0
 Acceleration is always g = -9.80 m/s2
vo= 0 (drop)
vo< 0 (throw)
a = g
v = 0
a = g

13. 08/11/2024 13
A ball is thrown downward (not dropped) from the top of a
tower. After being released, its downward acceleration will
be:
1. greater than g
2. exactly g
3. smaller than g
Throwing Down Question

14. 08/11/2024 14
Example 2
A ball is thrown vertically upward. At the very top of its trajectory, which of the
following statements is true:
1. velocity is zero and acceleration is zero
2. velocity is not zero and acceleration is zero
3. velocity is zero and acceleration is not zero
4. velocity is not zero and acceleration is not zero correct
Acceleration is the change in velocity. Just because the
velocity is zero does not mean that it is not changing.
At the top of the path, the velocity of the ball is zero,
but the acceleration is not zero. The velocity at the top
is changing, and the acceleration is the rate at which
velocity changes.
Acceleration is not zero since it is due to gravity
and is always a downward-pointing vector.

15. 08/11/2024 15
Dennis and Carmen are standing on the edge of a cliff.
Dennis throws a basketball vertically upward, and at the
same time Carmen throws a basketball vertically downward
with the same initial speed. You are standing below the cliff
observing this strange behavior. Whose ball is moving fastest
when it hits the ground?
1. Dennis' ball
2. Carmen's ball
3. Same
v0
v0
Dennis
Carmen
H
vA vB
Example 3A
Correct: v2
= v0
2
-2gΔy
On the dotted line:
Δy=0 ==> v2
= v0
2
v = ±v0
When Dennis’s ball returns
to dotted line its v = -v0
Same as Carmen’s

16. 08/11/2024 16
Dennis and Carmen are standing on the edge of a cliff. Dennis throws a
basketball vertically upward, and at the same time Carmen throws a basketball
vertically downward with the same initial speed. You are standing below the cliff
observing this strange behavior. Whose ball hits the ground at the base of the
cliff first?
1. Dennis' ball
2. Carmen's ball
3. Same
Example 3B
correct
v0
v0
Dennis
Carmen
y=y0
vA vB
y=0
Time for Dennis’s ball to return to the dotted
line:
v = v0 - g t
v = -v0
t = 2 v0 / g
This is the extra time taken by Dennis’s ball

17. 08/11/2024 17
Example 4
An object is dropped from rest. If it falls a distance D in time t then
how far will if fall in a time 2t ?
1. D/4
2. D/2
3. D
4. 2D
5. 4D Correct x=1/2 at2
Follow-up question: If the object has speed v at
time t then what is the speed at time 2t ?
1. v/4
2. v/2
3. v
4. 2v
5. 4v
Correct v=at

18. 08/11/2024 18
Which of the following statements is most nearly correct?
1 - A car travels around a circular track with constant velocity.
2 - A car travels around a circular track with constant speed.
3- Both statements are equally correct.
Example 5
correct
The direction of the velocity changes when going around circle.
• Speed is the magnitude of velocity -- it does not have a
direction and therefore does not change