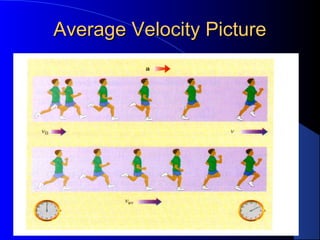
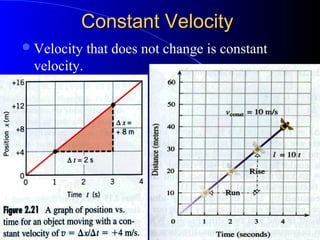
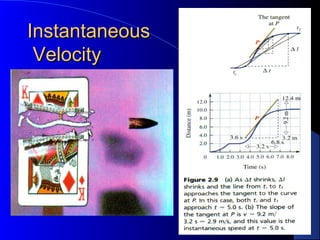
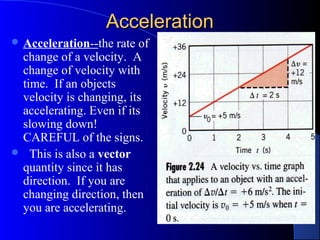
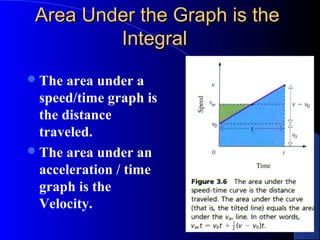
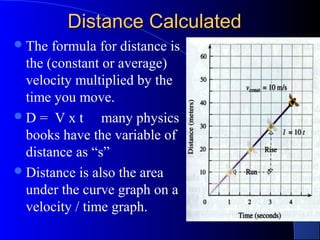
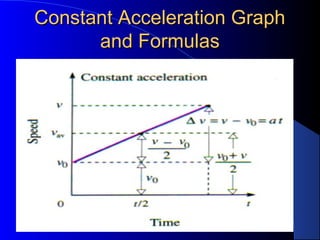
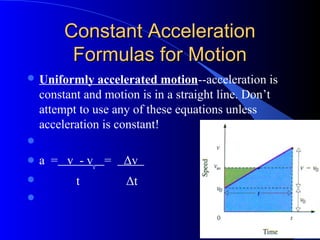
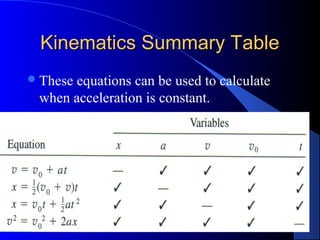
This document provides an overview of physics concepts related to motion and vectors, including: 1) Definitions of key terms like velocity, acceleration, displacement, distance, scalars and vectors. Equations for calculating average and instantaneous velocity and acceleration are presented. 2) Discussion of frames of reference, different types of motion problems (free fall, projectile motion, etc.), and how to apply kinematic equations for constant acceleration. 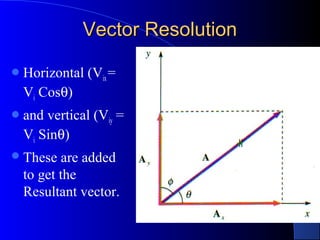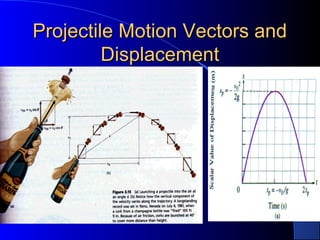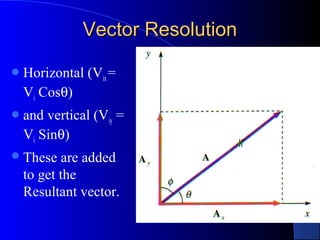3) Explanations of vector concepts like addition of vectors graphically and using trigonometry, projectile motion, and perpendicular independence of horizontal and vertical components of motion.

1. Physics - Motion and VectorsPhysics - Motion and Vectors
CHHS - Mr. Puckett

2. Velocity and AccelerationVelocity and Acceleration
ObjectivesObjectives
Define velocity and acceleration
operationally.
Relate the direction and magnitude of
velocity and acceleration vectors to the
motion of objects.
Create pictorial and physical models for
solving motion problems.

3. REFERENCE FRAMES ANDREFERENCE FRAMES AND
DISPLACEMENTDISPLACEMENT
Frames of reference--standard for
comparison. With respect to any
movement of position, distance,
or speed is made against a frame
of reference. With respect to the
Earth@ is most common.

4. Frame of ReferenceFrame of Reference
 Consider the
following case of
the aircraft moving
in relation to the
earth and then the
missiles moving
relative to the
plane and then the
earth.

5. Various Reference FramesVarious Reference Frames
1. The Earth.
2. Cartesian Coordinate Axis : X, Y and Z –
three perpendicular number lines used in all of
math and geometry. Origin is zero.
3. Up (+) and Down Vertical (-)
4. Cardinal points on a compass --North, South ,
East, and West

6. VECTORS vs SCALARSVECTORS vs SCALARS
 Vectors have BOTH magnitude (size) and
direction. The are represented by arrows.
 Vectors have both magnitude AND direction
while Scalars have only magnitude.
 Velocity, displacement, force and momentum
are vectors.
 Speed, distance, mass, time and temperature
are scalar quantities.
 Vectors--arrows drawn to show direction and
the length of the arrow is the magnitude

7. Vector vs. ScalarVector vs. Scalar
 When measuring
motion we must
distinguish between a
vector quantity and a
scalar quantity.
 A scalar has only
magnitude.
 A vector has both
magnitude and
direction.

8. DisplacementDisplacement
Displacement
is a change in
position.

9. Distance vs. DisplacementDistance vs. Displacement
 Distance--total ground
covered--consider your
route to school--total
mileage put on your
car/bike/feet. Scalar
 Displacement--change in
position of object from
starting point only– “as the
crow flies” from your house
to school. Vector
 Going in a circle yields 0
displacement and 2πr
distance.

10. What is Velocity?What is Velocity?
Velocity is a measure of the speed and
direction of the motion of an object.
As it is measuring both speed and direction,
it is a vector quantity.
The velocity magnitude is given as
displacement over time.

11. Average VelocityAverage Velocity
 AVERAGE VELOCITY
 You can no longer use the words speed and velocity
casually. They have very specific meanings.
 Speed--how far an object travels in a given time; how fast
it is moving. It is a scalar quantity.
 average speed =
 distance traveled = d = meters
time elapsed t second

12. Average Velocity PictureAverage Velocity Picture

13. Constant VelocityConstant Velocity
Velocity that does not change is constant
velocity.

14. INSTANTANEOUS VELOCITYINSTANTANEOUS VELOCITY
 Instantaneous velocity--The average velocity
over an infinitesimally short time interval.
 The slope of the position /time graph at one place
is the instantaneous velocity. This is calculus.
 v = limit Δx
 Δt->0 Δt
 That limit thing just means we want Δx as close to
zero as possible without it being zero.

15. InstantaneousInstantaneous
VelocityVelocity

16. Average vs. InstantaneousAverage vs. Instantaneous
 Average velocity is
velocity over a time
interval.
 v ≡ Δd/Δt =
 (d1-d0) /
(t1-t0).
 Note that the average
speed is the ratio of the
total distance traveled
over the total time, and is
a scalar.
 Instantaneous velocity is
at a specific point in time.
One of the problems with
the average velocity is that
it tells what happens over
a time interval. It does
NOT tell what happened
DURING the interval.
 v, with no bar over it, is
the instantaneous velocity.

17. Negative VelocityNegative Velocity
Note that the cars on the
bridge are going both
directions. This would be
negative velocity.

18. AccelerationAcceleration
 Acceleration--the rate of
change of a velocity. A
change of velocity with
time. If an objects
velocity is changing, its
accelerating. Even if its
slowing down!
CAREFUL of the signs.
 This is also a vector
quantity since it has
direction. If you are
changing direction, then
you are accelerating.

19. Acceleration ExampleAcceleration Example

20. Calculation AccelerationCalculation Acceleration
 Average Acceleration = the change of velocity
divided by the change in time. The formula is :
a= Δv / Δt
 Example: If you are driving and start from a stop
sign (v=0) and accelerate for 5 seconds and have a
velocity of 25 m/s then your acceleration is (25
m/s – 0 m/s divided by (5 sec – 0 sec) for an
average acceleration of 5 m/s2

21. Acceleration FormulaAcceleration Formula
 Average acceleration = a =
 change of velocity = Δv = meters
time elapsed Δt second2

22. Instantaneous AccelerationInstantaneous Acceleration
 Instantaneous acceleration---The average
change in velocity over an infinitesimally short
time interval.
 a = limit Δv
 Δt0 Δt

 NOTE THAT ACCELERATION TELLS US
HOW FAST THE VELOCITY CHANGES,
WHEREAS VELOCITY TELLS US HOW
FAST THE POSITION CHANGES.

23. Constant AccelerationConstant Acceleration
Formulas for MotionFormulas for Motion
 Uniformly accelerated motion--acceleration is
constant and motion is in a straight line. Don’t
attempt to use any of these equations unless
acceleration is constant!

 a = v - vo
= Δv
 t Δt


24. Area Under the Graph is theArea Under the Graph is the
IntegralIntegral
The area under a
speed/time graph is
the distance
traveled.
The area under an
acceleration / time
graph is the
Velocity.

25. Velocity & Position EquationsVelocity & Position Equations
 To solve for velocity of an object at a
certain time with constant acceleration:
vf = vo
+ at
To calculate position of an object after a time, t,
when it’s undergoing constant acceleration. Can
also show vertical Y vectors:

xf = xo
+ vo
t + 1/2 at2


26. Velocity Without Time KnownVelocity Without Time Known
To calculate velocity, acceleration or position
when time is NOT known:
v2
f = vo
2
+ 2a (xf - xo
)

 vo
equals ZERO when the object begins
its acceleration from rest--this is your
friend! It simplified things!

27. Kinematics Summary TableKinematics Summary Table
These equations can be used to calculate
when acceleration is constant.

28. Free FallFree Fall
Free Fall is
constant
acceleration toward
the earth. In intro
physics we ignore
air drag.
Formula here is dy
= ½ gt2
because it
started with 0 m/s
vertical velocity.

29. Free Fall and GravityFree Fall and Gravity
 The most famous constant acceleration is that due
to gravity. Memorize its value a = g = -9.80 m/s2
=
-32 ft/s2
.
 What falls faster, a rock or a feather?
– Neither, in a vacuum. Your experience is that the
feather would fall more slowly. That=s entirely due to
air resistance.
 Galileo--Father of Modern Science. It was he that
stated at a given location on Earth and in the
absence of air resistance, all objects fall at a
constant acceleration, g, 9.80 m/s2
.

30. Free Fall with gravityFree Fall with gravity
Gravity causes all objects to accelerate
toward the earth at 9.8 m/s2
Objects in free fall will not accelerate
forever; air drags on the object and slows
the acceleration to a constant velocity called
: “ Terminal Velocity”
About 120 mph
For humans

31. Calculating Velocity of aCalculating Velocity of a
Falling ObjectFalling Object
 1. We ignore the drag of air in our calculations.
(Calculus-changing rates)
 2. Equation: v = gt means velocity of a falling
body is the acceleration of gravity times the fall
time.
 3. Example: If you drop a rock off a 500 m cliff:
How fast is it going after 3 seconds? V = gt =
(10m/s2
) X 3sec = 30 m/s

32. Parasitic AirParasitic Air
DragDrag
When astronauts
went to the moon
they dropped a
hammer and feather
and they fell at the
same rate. There
was no air to slow
the feather down.

33. Terminal Velocity & G-ForcesTerminal Velocity & G-Forces
 ! The speed of a falling object in air or
any other fluid does NOT increase indefinitely. If
the object falls far enough, it will reach a
maximum velocity called the terminal velocity.
 ! Acceleration due to gravity is a vector
(as is any acceleration) and its direction, is
downward, toward the center of the Earth.
 ! The acceleration of rockets and fast
airplanes is often expressed in g’s. Three g’s is
equal to 3 x 9.8 m/s2
= 29.4 m/s2
.

34. Ball TossBall Toss
A vertical
ball toss
undergoes
constant
acceleration
but variable
velocity.

35. Straight Up and DownStraight Up and Down
KinematicsKinematics
Apex is the highest point of the trajectory
above the ground where a ball stops. At
that point the vertical velocity is = ZERO
Acceleration is gravity.
Time to top of trajectory: T ½ = -voy/g
Total Time aloft from ground = - 2voy / g
Apex Formula = dyf = yo + voyt + ½ gt2
or
dyf = - voy
2
/ 2g

36. Vertical Motion Problem TypesVertical Motion Problem Types
1. Drop Problem: Viy = 0. dy=½gt2
and vf
= vo + gt.
2. Ground to ground: Time to top (T½) =
-Voy/g, Total time aloft (Tt) = T½x 2 . Dapex=
vot + ½gt2
3. Elevated Ground to ground: Starts on
elevated position up to apex
Dapex=Yo + vot + ½gt2
and then a drop problem
on downside.

37. The Cliff TossThe Cliff Toss
 Two examples of free fall motion are
shown in the following cliff toss.
Each will vary in time aloft and final
velocity.
 A. The pellet is shot down at 30
 B. The pellet is shot up at 30 m/s and
then falls back down with equal
velocity.
 C. A third classic problem is the
horizontal throw starts with 0 m/s
vertical velocity and drops.

38. ADDITION OF VECTORSADDITION OF VECTORS
Graphical, -tip to tail. If the motion or force is
along a straight line, simply add the two or
more lengths to get the resultant.

39. Graphical Non –Graphical Non –
Parallel VectorParallel Vector
AdditionAddition
More often, the motion or
force is not simply linear.
That’s where trig. comes
in. You can use the tip to
tail graphical method,
BUT you’ll need a ruler
and a protractor.

40. Trigonometry FunctionsTrigonometry Functions
 ! Use trig. functions-- a mnemonic for sin, cos,
and tan is SOH CAH TOA.

 O = Opposite = sin
 H Hypotenuse

 A = Adjacent = cos
 H Hypotenuse

 O = Opposite = tan
 A Adjacent

41. Mathematical Addition of Non-Mathematical Addition of Non-
Perpendicular VectorsPerpendicular Vectors
1. Resolve initial vectors into the horizontal (Vix= Vi
Cosθ) and vertical (Viy = Vi Sinθ) components.
This is Vector Resolution.
2. Add the x components from the different vectors
for an X total. Repeat with y.
3. Use Pythagorean to add the x and y totals: R2
=
X2
+ Y2
and this is the Resultant.
4. Use Tangent to find the angle: Tan θ= Y total
Xtotal
5. The Resultant and angle θ are the Vector Sum.

42. Vector ResolutionVector Resolution
Horizontal (Vix=
Vi Cosθ)
and vertical (Viy =
Vi Sinθ)
These are added
to get the
Resultant vector.

43. Distance CalculatedDistance Calculated
The formula for distance is
the (constant or average)
velocity multiplied by the
time you move.
D = V x t many physics
books have the variable of
distance as “s”
Distance is also the area
under the curve graph on a
velocity / time graph.

44. Projectile MotionProjectile Motion
The natural
motion of
an object
that is
thrown/lau
nched is
called
projectile
motion.

45. Projectile Motion Vectors andProjectile Motion Vectors and
DisplacementDisplacement

46. Vector ResolutionVector Resolution
Horizontal (Vix=
Vi Cosθ)
and vertical (Viy =
Vi Sinθ)
These are added
to get the
Resultant vector.

47. Calculate Projectile MotionCalculate Projectile Motion
 Range = horizontal distance traveled by the
trajectory of a projectile. We ignore air friction: =
constant velocity. Range Formula: Either R =
dx = vi cosθt (time aloft) from d = vt before.
 Apex is the highest point of the trajectory above
the ground. Acceleration is gravity. Apex
Formula = Dy = yo + voyt + ½ gt2
or = - vo
2
/ 2g
 Time to top of trajectory: T ½ = -voy/g
 Total Time aloft = - 2visinθ / g

48. Perpendicular VectorPerpendicular Vector
IndependenceIndependence
Note in the diagram below that the initial
horizontal velocity varies and it changes the
range that the ball travels. But the Vertical
vector remains constant throughout all shots

49. Constant Acceleration GraphConstant Acceleration Graph
and Formulasand Formulas

50. Review Velocity FormulasReview Velocity Formulas
 1. v = vo
+ at this one has initial and final
velocity, time and acceleration.
 2. x = xo
+ vo
t + ½ at2
This one has initial
and final distance, velocity, time and
acceleration.
 3. v2
= vo
2
+ 2a (x-xo
) This one has initial
and final velocity, acceleration and initial and
final distance.
 4. a = ∆v / ∆t This one has acceleration,
velocity and time.
 5. V = ∆d/∆t this one has velocity,
distance and time

51. Graphing MotionGraphing Motion
One of the best ways to describe motion is
with graphs.
There are 3 kinds of graphs we need to look
at:
– Position vs. Time graphs
– Velocity vs. Time graphs
– Acceleration vs. Time graphs

52. Position Vs. Time GraphPosition Vs. Time Graph
In this graph you are graphic the physical
location vs. time for an object.
The slope of the graph is the velocity.
 v = Δd / Δt

53. Velocity Vs. Time GraphVelocity Vs. Time Graph
This graph shows the velocity of an object
at any point in time.
The slope of the graph is Acceleration.
 a = Δv/ Δt
 The area under the curve is the distance
traveled.

54. Acceleration Vs. Time GraphAcceleration Vs. Time Graph
This graph shows the acceleration of an
object at any point in time.
 The area under the curve is the velocity.