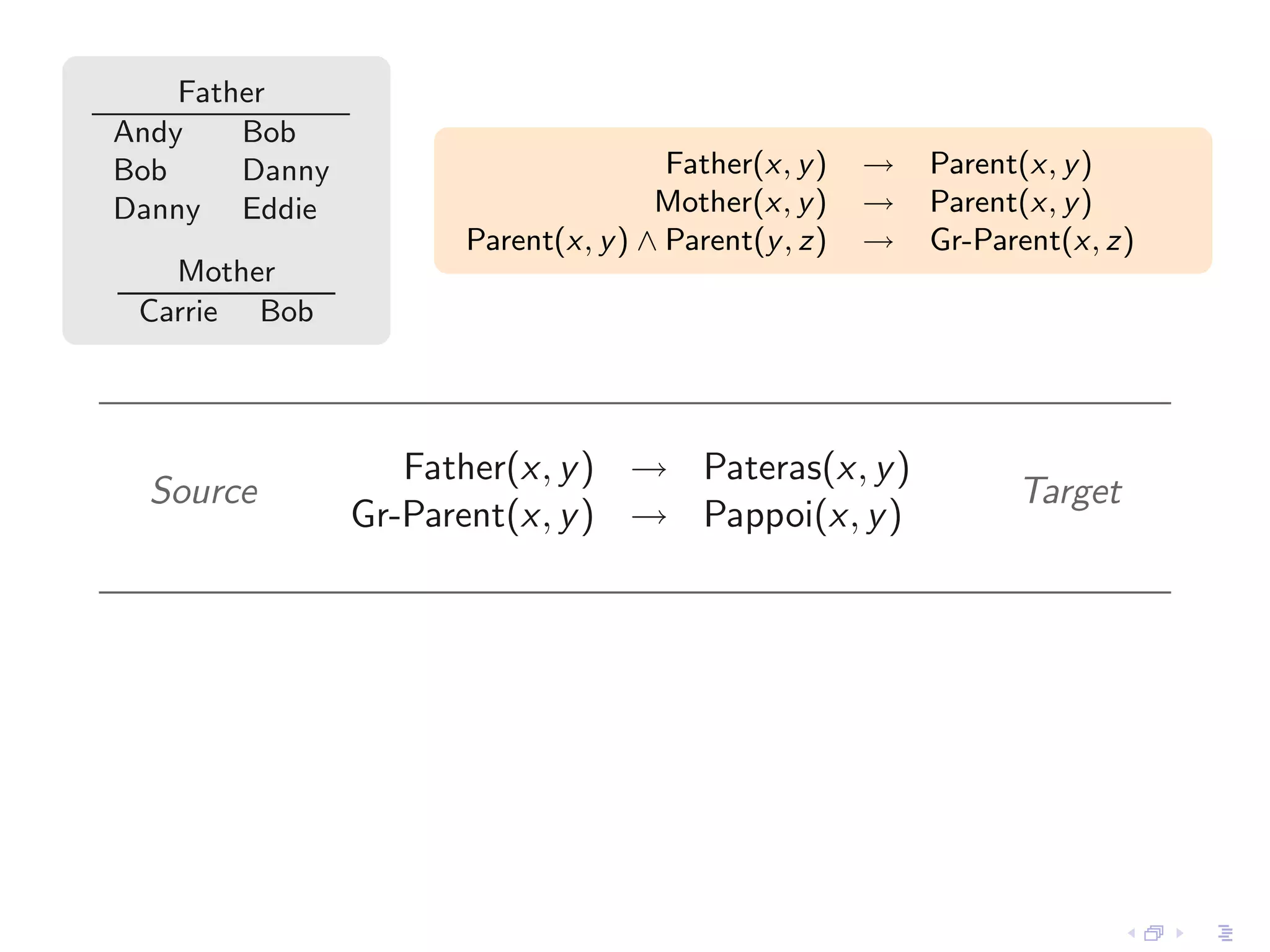
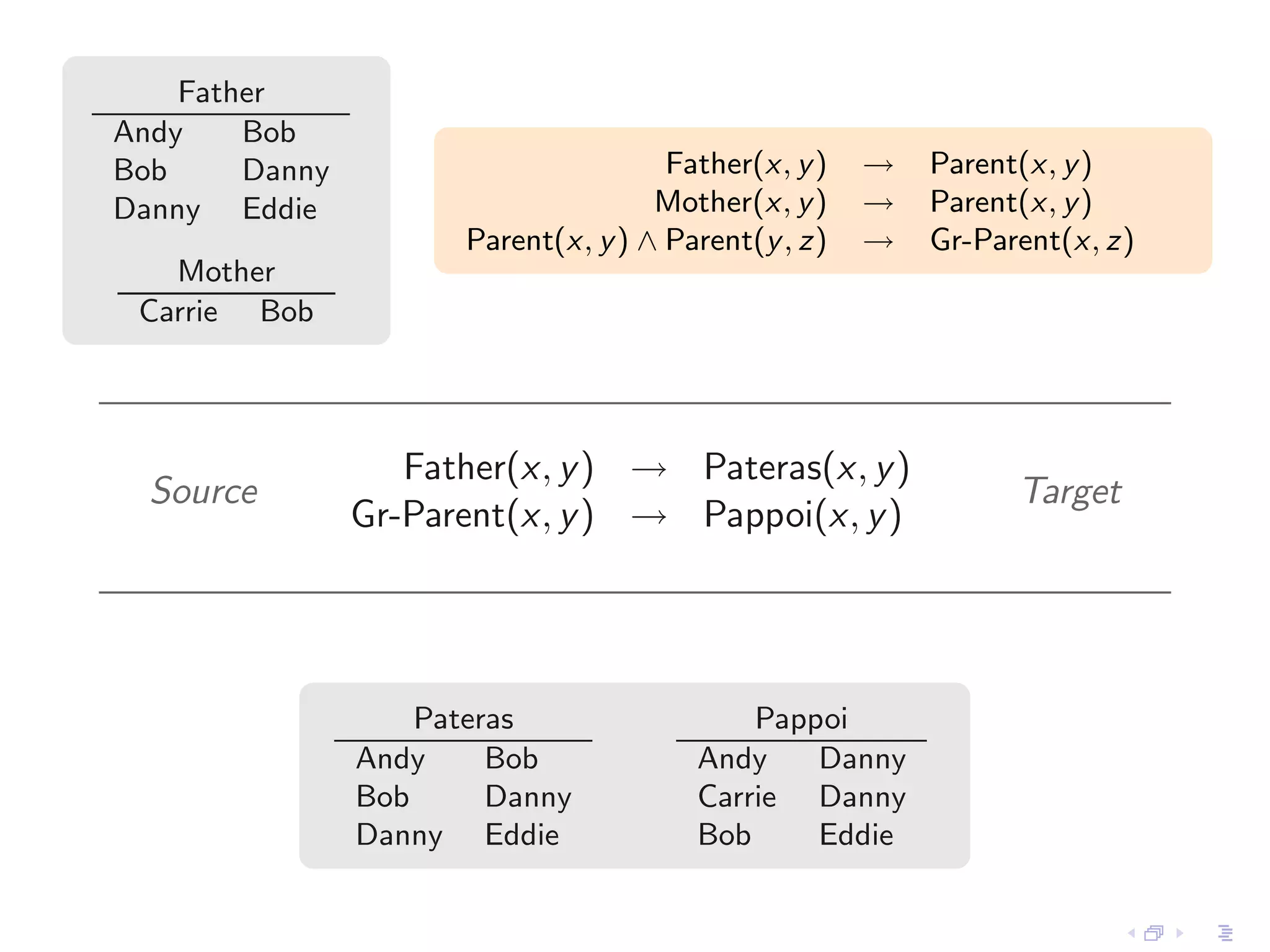
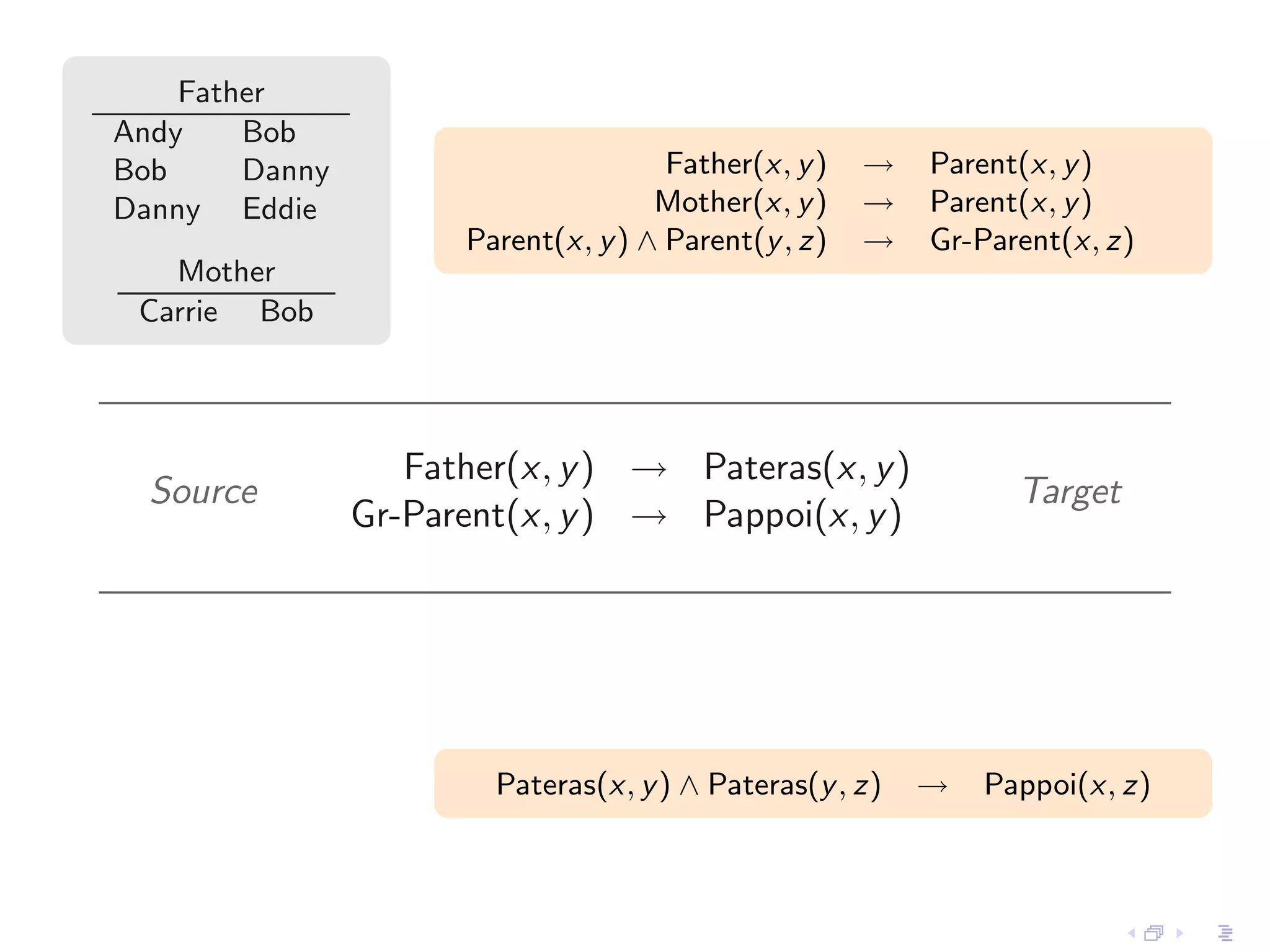
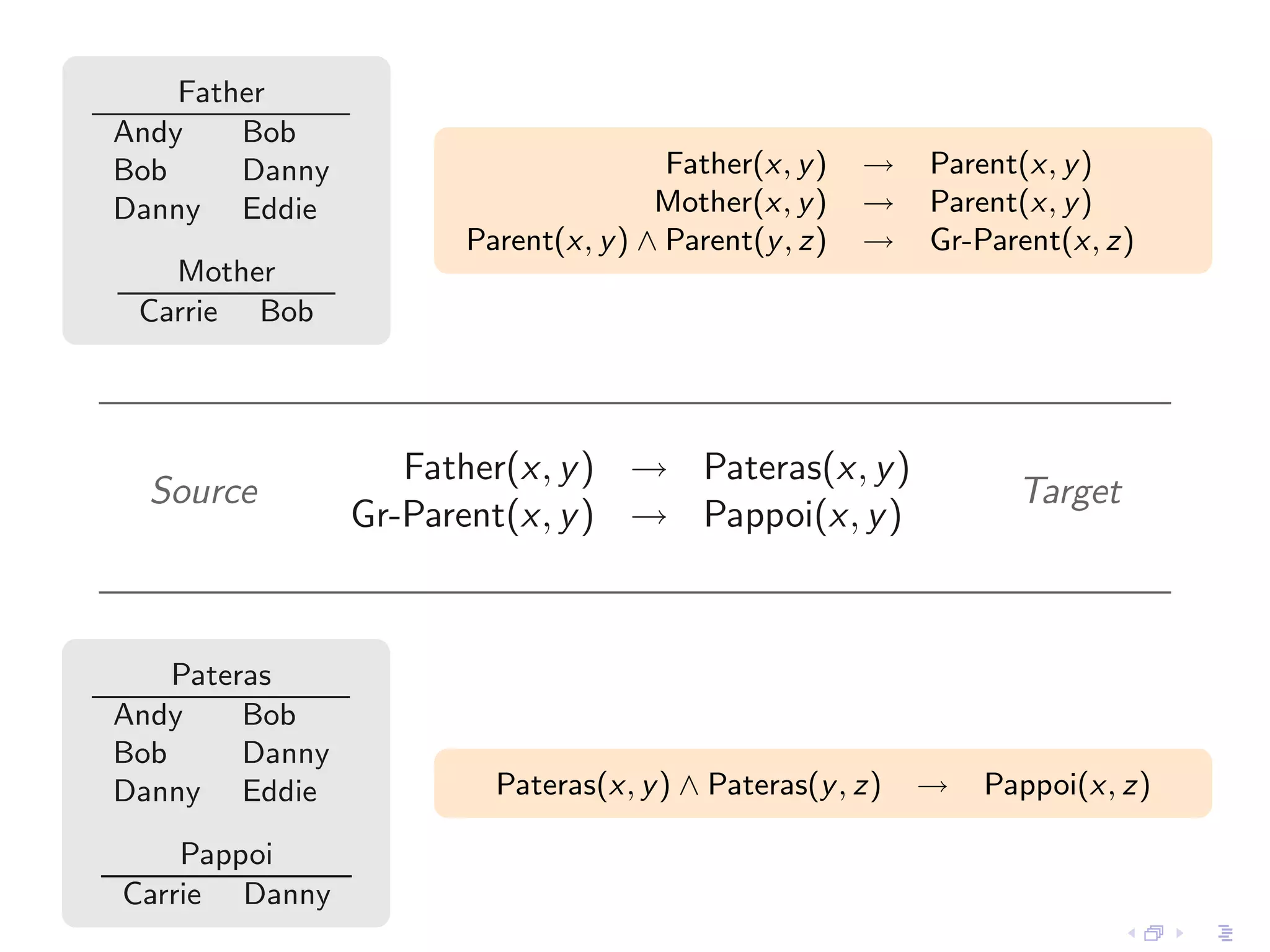
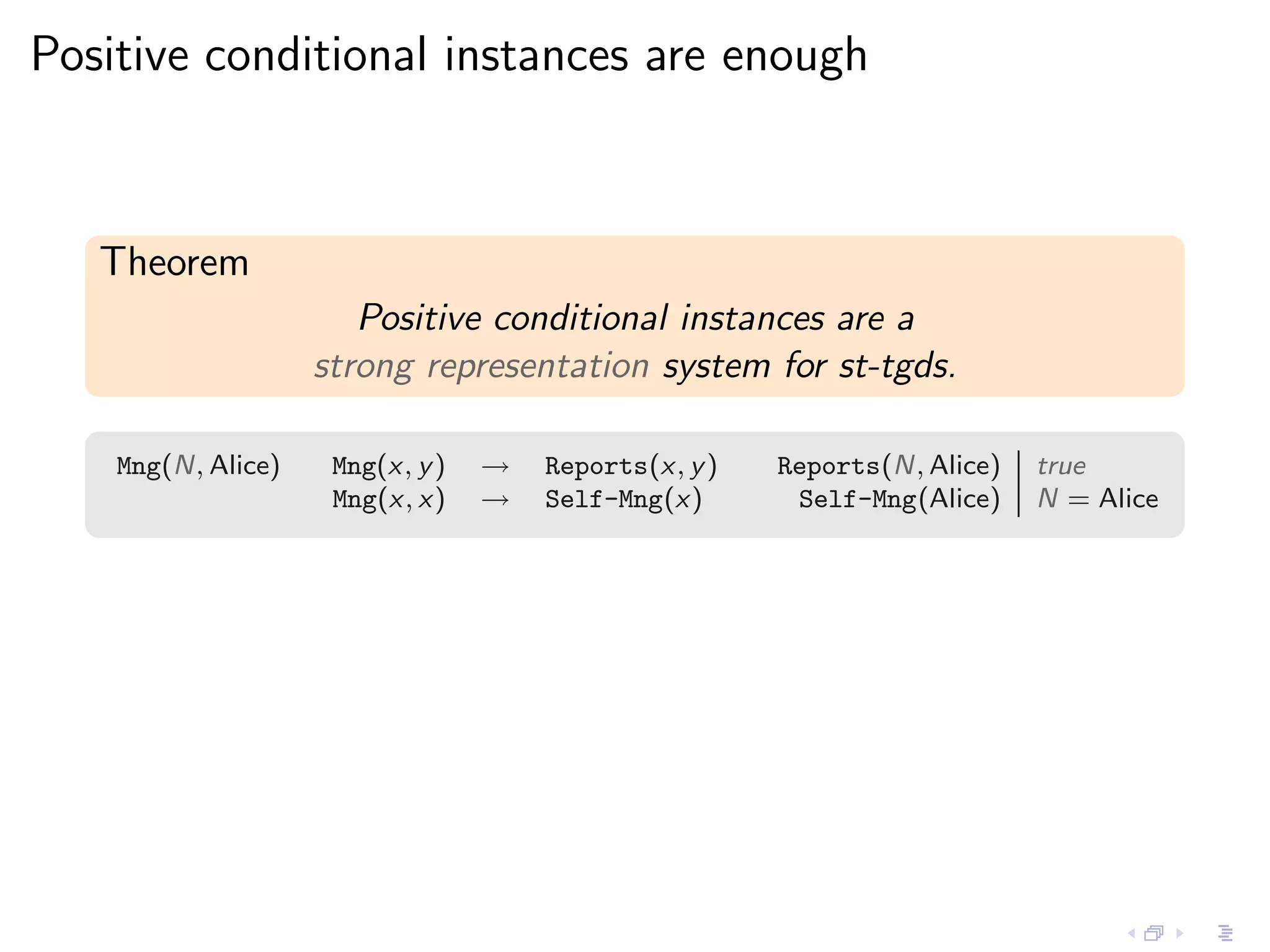
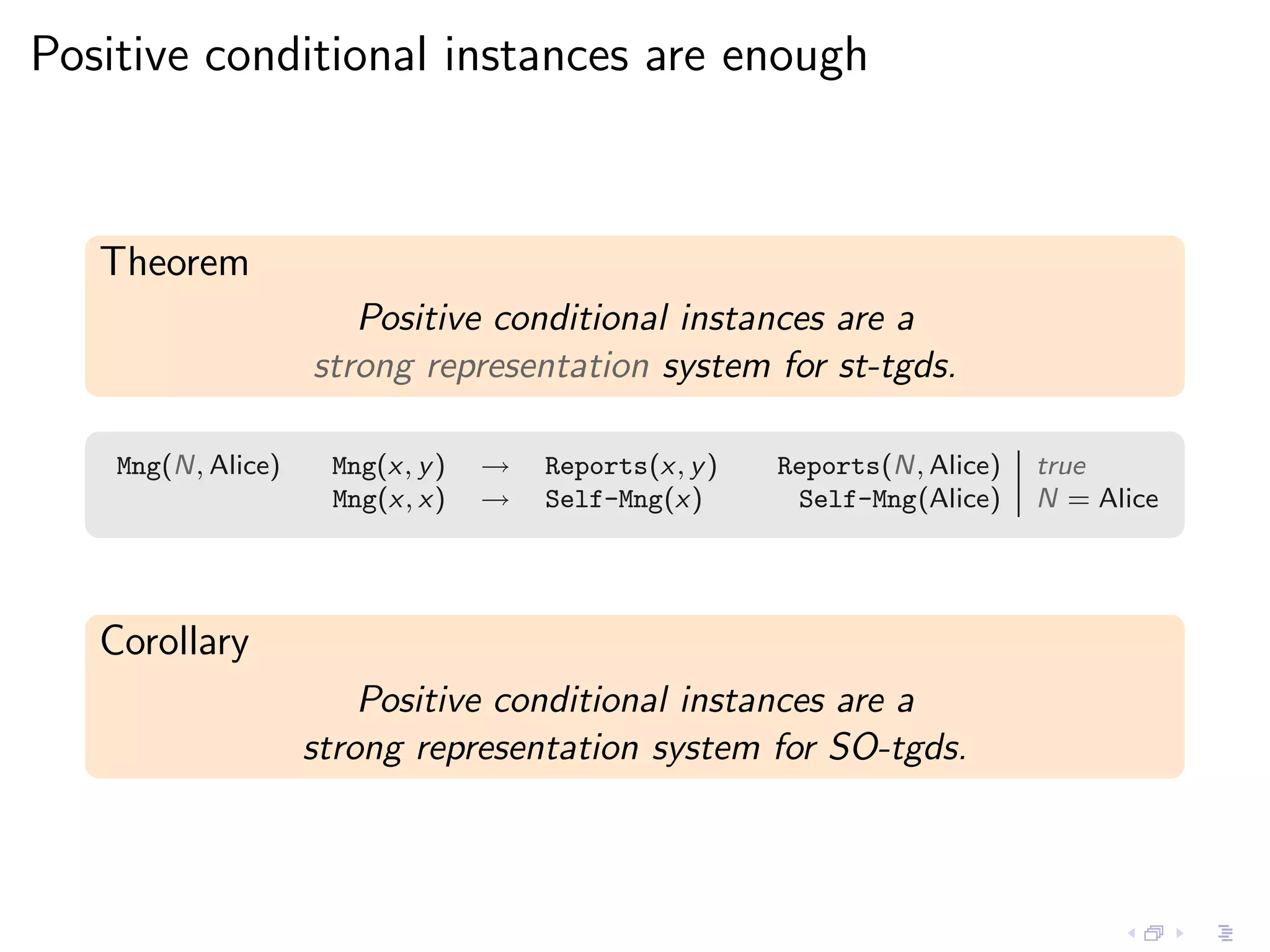
- The document discusses exchanging more than just complete data between databases, by using representation systems that can capture sets of possible instances. - It proposes a formalism for exchanging representations between systems and applies this to incomplete instances and knowledge bases. - Incomplete instances like those with null values or constraints can be represented as representation systems, and positive conditional instances form a strong representation system for schema mappings specified by source-to-target tuple-generating dependencies.

1. Exchanging More than Complete Data
Jorge P´rez
e
Universidad de Chile
joint work with Marcelo Arenas (PUC-Chile) and Juan Reutter (Univ. Edinburgh)

2. Father
Andy Bob
Bob Danny Father(x, y ) → Parent(x, y )
Danny Eddie Mother(x, y ) → Parent(x, y )
Parent(x, y ) ∧ Parent(y , z) → Gr-Parent(x, z)
Mother
Carrie Bob

3. Father
Andy Bob
Bob Danny Father(x, y ) → Parent(x, y )
Danny Eddie Mother(x, y ) → Parent(x, y )
Parent(x, y ) ∧ Parent(y , z) → Gr-Parent(x, z)
Mother
Carrie Bob
Father(x, y ) → Pateras(x, y )
Source Target
Gr-Parent(x, y ) → Pappoi(x, y )

4. Father
Andy Bob
Bob Danny Father(x, y ) → Parent(x, y )
Danny Eddie Mother(x, y ) → Parent(x, y )
Parent(x, y ) ∧ Parent(y , z) → Gr-Parent(x, z)
Mother
Carrie Bob
Father(x, y ) → Pateras(x, y )
Source Target
Gr-Parent(x, y ) → Pappoi(x, y )
Pateras Pappoi
Andy Bob Andy Danny
Bob Danny Carrie Danny
Danny Eddie Bob Eddie

5. Father
Andy Bob
Bob Danny Father(x, y ) → Parent(x, y )
Danny Eddie Mother(x, y ) → Parent(x, y )
Parent(x, y ) ∧ Parent(y , z) → Gr-Parent(x, z)
Mother
Carrie Bob
Father(x, y ) → Pateras(x, y )
Source Target
Gr-Parent(x, y ) → Pappoi(x, y )
Pateras(x, y ) ∧ Pateras(y , z) → Pappoi(x, z)

6. Father
Andy Bob
Bob Danny Father(x, y ) → Parent(x, y )
Danny Eddie Mother(x, y ) → Parent(x, y )
Parent(x, y ) ∧ Parent(y , z) → Gr-Parent(x, z)
Mother
Carrie Bob
Father(x, y ) → Pateras(x, y )
Source Target
Gr-Parent(x, y ) → Pappoi(x, y )
Pateras
Andy Bob
Bob Danny
Danny Eddie Pateras(x, y ) ∧ Pateras(y , z) → Pappoi(x, z)
Pappoi
Carrie Danny

7. Exchanging More than Complete Data
Jorge P´rez
e
Universidad de Chile
joint work with Marcelo Arenas (PUC-Chile) and Juan Reutter (Univ. Edinburgh)

8. We can exchange more than complete data
◮ In data exchange we begin with a database instance
we begin with complete data
◮ What if we have a representation of a set of
possible instances?
◮ We propose a new general formalism to exchange
representations of possible instances
and apply it to incomplete instances and knowledge bases

9. Outline
Formalism for exchanging representations systems
Applications to incomplete instances
Applications to knowledge bases
What is the complexity of testing kb-solutions?
How can we compute a good kb-solution?
Concluding remarks

10. Outline
Formalism for exchanging representations systems
Applications to incomplete instances
Applications to knowledge bases
What is the complexity of testing kb-solutions?
How can we compute a good kb-solution?
Concluding remarks

11. Representation systems
A representation system is composed of:
◮ a set W of representatives
◮ a function rep from W to sets of instances
rep
V −→ {I1 , I2 , I3 , . . .} = rep(V)

12. Representation systems
A representation system is composed of:
◮ a set W of representatives
◮ a function rep from W to sets of instances
rep
V −→ {I1 , I2 , I3 , . . .} = rep(V)
◮ Incomplete instances and knowledge bases are
representation systems

13. In classical data exchange
we consider only complete data
M = (S, T, Σ) a schema mapping from S to T
I ∈ Inst(S), J ∈ Inst(T)
J is a solution for I under M iff (I , J) |= Σ
J ∈ SolM (I )

14. In classical data exchange
we consider only complete data
M = (S, T, Σ) a schema mapping from S to T
I ∈ Inst(S), J ∈ Inst(T)
J is a solution for I under M iff (I , J) |= Σ
J ∈ SolM (I )
We can extend this to set of instances:
given a set X ⊆ Inst(S)
SolM (X ) = SolM (I )
I ∈X

15. Extending the definition to representation systems
Given:
◮ a mapping M = (S, T, Σ)
◮ a representation system R = (W, rep)
◮ U, V ∈ W

16. Extending the definition to representation systems
Given:
◮ a mapping M = (S, T, Σ)
◮ a representation system R = (W, rep)
◮ U, V ∈ W
Definition
U is an R-solution of V if
rep(U) ⊆ SolM (rep(V))

17. Extending the definition to representation systems
Given:
◮ a mapping M = (S, T, Σ)
◮ a representation system R = (W, rep)
◮ U, V ∈ W
Definition
U is an R-solution of V if
rep(U) ⊆ SolM (rep(V))
or equivalently,
∀J ∈ rep(U), ∃I ∈ rep(V) such that J ∈ SolM (I )

18. Universal solutions and strong representation systems
Definition
U is a universal R-solution of V if
rep(U) = SolM (rep(V))

19. Universal solutions and strong representation systems
Definition
U is a universal R-solution of V if
rep(U) = SolM (rep(V))
Let C be a class of mappings,
Definition
R = (W, rep) is a strong representation system for C if
for every M ∈ C, and V ∈ W, there exists a U ∈ W such that:
rep(U) = SolM (rep(V))

20. Universal solutions and strong representation systems
Definition
U is a universal R-solution of V if
rep(U) = SolM (rep(V))
Let C be a class of mappings,
Definition
R = (W, rep) is a strong representation system for C if
for every M ∈ C, and V ∈ W, there exists a U ∈ W such that:
rep(U) = SolM (rep(V))
Strong representation systems ⇒ universal solutions for
representatives in R can always be represented in the same system.

21. Outline
Formalism for exchanging representations systems
Applications to incomplete instances
Applications to knowledge bases
What is the complexity of testing kb-solutions?
How can we compute a good kb-solution?
Concluding remarks

22. Incomplete Instances
We consider:
◮ Naive instances: instances with null values
R(1, N1 )
R(N1 , 2)

23. Incomplete Instances
We consider:
◮ Naive instances: instances with null values
R(1, N1 )
R(N1 , 2)
◮ Positive conditional instances: naive instances plus
conditions for tuples
◮ equalities between nulls, and between nulls and constants
◮ conjunctions and disjunctions
T (1, N1 ) true
R(1, N1 , N2 ) N1 = N2 ∨ (N1 = 2 ∧ N2 = 3)

24. Incomplete Instances
We consider:
◮ Naive instances: instances with null values
R(1, N1 )
R(N1 , 2)
◮ Positive conditional instances: naive instances plus
conditions for tuples
◮ equalities between nulls, and between nulls and constants
◮ conjunctions and disjunctions
T (1, N1 ) true
R(1, N1 , N2 ) N1 = N2 ∨ (N1 = 2 ∧ N2 = 3)
Semantics given by valuations of nulls (+ open world):
rep(I) = {K | µ(I) ⊆ K for some valuation µ}

25. Strong representation systems for st-tgds
Let M = (S, T, Σ) be specified by source-to-target tgds
(st-tgd: φS (¯ ) → ∃¯ψT (¯ , y ), φS and ψT are CQs)
x y x ¯
(FKMP03)
For every complete instance I there exists a naive instance J s.t.
rep(J ) = SolM (I )

26. Strong representation systems for st-tgds
Let M = (S, T, Σ) be specified by source-to-target tgds
(st-tgd: φS (¯ ) → ∃¯ψT (¯ , y ), φS and ψT are CQs)
x y x ¯
(FKMP03)
For every complete instance I there exists a naive instance J s.t.
rep(J ) = SolM (I )
Proposition
Naive instances are not a strong representation system for st-tgds
Idea
Mng(N, Alice) Mng(x, y ) → Reports(x, y )
Mng(x, x) → Self-Mng(x)

27. Strong representation systems for st-tgds
Let M = (S, T, Σ) be specified by source-to-target tgds
(st-tgd: φS (¯ ) → ∃¯ψT (¯ , y ), φS and ψT are CQs)
x y x ¯
(FKMP03)
For every complete instance I there exists a naive instance J s.t.
rep(J ) = SolM (I )
Proposition
Naive instances are not a strong representation system for st-tgds
Idea
Mng(N, Alice) Mng(x, y ) → Reports(x, y ) ?
Mng(x, x) → Self-Mng(x)

28. Positive conditional instances are enough
Theorem
Positive conditional instances are a
strong representation system for st-tgds.

29. Positive conditional instances are enough
Theorem
Positive conditional instances are a
strong representation system for st-tgds.
Mng(N, Alice) Mng(x, y ) → Reports(x, y )
Mng(x, x) → Self-Mng(x)

30. Positive conditional instances are enough
Theorem
Positive conditional instances are a
strong representation system for st-tgds.
Mng(N, Alice) Mng(x, y ) → Reports(x, y ) Reports(N, Alice) true
Mng(x, x) → Self-Mng(x)

31. Positive conditional instances are enough
Theorem
Positive conditional instances are a
strong representation system for st-tgds.
Mng(N, Alice) Mng(x, y ) → Reports(x, y ) Reports(N, Alice) true
Mng(x, x) → Self-Mng(x) Self-Mng(Alice)

32. Positive conditional instances are enough
Theorem
Positive conditional instances are a
strong representation system for st-tgds.
Mng(N, Alice) Mng(x, y ) → Reports(x, y ) Reports(N, Alice) true
Mng(x, x) → Self-Mng(x) Self-Mng(Alice) N = Alice

33. Positive conditional instances are enough
Theorem
Positive conditional instances are a
strong representation system for st-tgds.
Mng(N, Alice) Mng(x, y ) → Reports(x, y ) Reports(N, Alice) true
Mng(x, x) → Self-Mng(x) Self-Mng(Alice) N = Alice
Corollary
Positive conditional instances are a
strong representation system for SO-tgds.

34. Positive conditional instances are
exactly the needed representation system
Theorem
Positive conditional instances are minimal:
◮ equalities between nulls
◮ equalities between constant and nulls
◮ conjunctions and disjunctions
are all needed for a strong representation system of st-tgds

35. Positive conditional instances
match the complexity bounds of classical data exchange
Theorem
For positive conditional instances and (fixed) st-tgds
◮ Universal solutions can be constructed in polynomial time.
◮ Certain answers of unions of conjunctive queries
can be computed in polynomial time.

36. Outline
Formalism for exchanging representations systems
Applications to incomplete instances
Applications to knowledge bases
What is the complexity of testing kb-solutions?
How can we compute a good kb-solution?
Concluding remarks

37. The semantics of knowledge bases
is given by sets of instances
Knowledge base over S: (I , Γ) s.t.
I ∈ Inst(S)
Γ a set of rules over S
Semantics: finite models
Mod(I , Γ) = {K ∈ Inst(S) | I ⊆ K and K |= Γ}

38. We can apply our formalism
to knowledge bases
(I2 , Γ2 ) is a kb-solution for (I1 , Γ1 ) under M iff
Mod(I2 , Γ2 ) ⊆ SolM (Mod(I1 , Γ1 ))

39. Outline
Formalism for exchanging representations systems
Applications to incomplete instances
Applications to knowledge bases
What is the complexity of testing kb-solutions?
How can we compute a good kb-solution?
Concluding remarks

40. We study the following decision problem
Check-KB-Sol:
Input: M = (S, T, Σ) with Σ st-tgds
(I1 , Γ1 ) knowledge base over S with Γ1 tgds
(I2 , Γ2 ) knowledge base over T with Γ2 tgds
Output: Is (I2 , Γ2 ) a kb-solution of (I1 , Γ1 ) under M?

41. We study the following decision problem
Check-KB-Sol:
Input: M = (S, T, Σ) with Σ st-tgds
(I1 , Γ1 ) knowledge base over S with Γ1 tgds
(I2 , Γ2 ) knowledge base over T with Γ2 tgds
Output: Is (I2 , Γ2 ) a kb-solution of (I1 , Γ1 ) under M?
Theorem
Check-KB-Sol is undecidable (even for fixed M).

42. We study the following decision problem
Check-KB-Sol:
Input: M = (S, T, Σ) with Σ st-tgds
(I1 , Γ1 ) knowledge base over S with Γ1 tgds
(I2 , Γ2 ) knowledge base over T with Γ2 tgds
Output: Is (I2 , Γ2 ) a kb-solution of (I1 , Γ1 ) under M?
Theorem
Check-KB-Sol is undecidable (even for fixed M).
Undecidability is a consequence of using ∃ in knowledge bases
Check-Full-KB-Sol: Γ1 , Γ2 full-tgds (no ∃)

43. The complexity of Check-Full-KB-Sol
Theorem
Check-Full-KB-Sol is EXPTIME-complete.

44. The complexity of Check-Full-KB-Sol
Theorem
Check-Full-KB-Sol is EXPTIME-complete.
Theorem
If M = (S, T, Σ) is fixed
Check-Full-KB-Sol is ∆P [O(log n)]-complete.
2
∆P [O(log n)]
2 ≡ P NP with only a logarithmic
number of calls to the NP oracle.

45. Hardness is obtained by reducing
the Max-Odd-Clique problem
Given a graph G with n nodes:
S: E (·, ·), Succ(·, ·), Clique(·)

46. Hardness is obtained by reducing
the Max-Odd-Clique problem
Given a graph G with n nodes:
S: E (·, ·), Succ(·, ·), Clique(·)
T: E ′ (·, ·), Succ ′ (·, ·), Clique ′ (·)

47. Hardness is obtained by reducing
the Max-Odd-Clique problem
Given a graph G with n nodes:
S: E (·, ·), Succ(·, ·), Clique(·)
T: E ′ (·, ·), Succ ′ (·, ·), Clique ′ (·)
I1 and I2 are copies of G , plus a successor relation over [1, n]

48. Hardness is obtained by reducing
the Max-Odd-Clique problem
Given a graph G with n nodes:
S: E (·, ·), Succ(·, ·), Clique(·)
T: E ′ (·, ·), Succ ′ (·, ·), Clique ′ (·)
I1 and I2 are copies of G , plus a successor relation over [1, n]
Γ1 : “E has a clique of even size x ≤ n” → Clique(x)

49. Hardness is obtained by reducing
the Max-Odd-Clique problem
Given a graph G with n nodes:
S: E (·, ·), Succ(·, ·), Clique(·)
T: E ′ (·, ·), Succ ′ (·, ·), Clique ′ (·)
I1 and I2 are copies of G , plus a successor relation over [1, n]
Γ1 : “E has a clique of even size x ≤ n” → Clique(x)
Γ2 : “E ′ has a clique of odd size x ≤ n” → Clique ′ (x)

50. Hardness is obtained by reducing
the Max-Odd-Clique problem
Given a graph G with n nodes:
S: E (·, ·), Succ(·, ·), Clique(·)
T: E ′ (·, ·), Succ ′ (·, ·), Clique ′ (·)
I1 and I2 are copies of G , plus a successor relation over [1, n]
Γ1 : “E has a clique of even size x ≤ n” → Clique(x)
Γ2 : “E ′ has a clique of odd size x ≤ n” → Clique ′ (x)
Σ: Clique(x) ∧ Succ(x, y ) → Clique ′ (y )

51. Hardness is obtained by reducing
the Max-Odd-Clique problem
Given a graph G with n nodes:
S: E (·, ·), Succ(·, ·), Clique(·)
T: E ′ (·, ·), Succ ′ (·, ·), Clique ′ (·)
I1 and I2 are copies of G , plus a successor relation over [1, n]
Γ1 : “E has a clique of even size x ≤ n” → Clique(x)
Γ2 : “E ′ has a clique of odd size x ≤ n” → Clique ′ (x)
Σ: Clique(x) ∧ Succ(x, y ) → Clique ′ (y )
(I2 , Γ2 ) is a kb-solution of (I1 , Σ1 ) iff
the maximum size of a clique in G is odd.

52. Outline
Formalism for exchanging representations systems
Applications to incomplete instances
Applications to knowledge bases
What is the complexity of testing kb-solutions?
How can we compute a good kb-solution?
Concluding remarks

53. Minimal knowledge bases as good kb-solutions
What are good knowledge-base solutions?
◮ first choice: universal kb-solutions, but
◮ there are some other kb-solutions desirable to materialize

54. Minimal knowledge bases as good kb-solutions
What are good knowledge-base solutions?
◮ first choice: universal kb-solutions, but
◮ there are some other kb-solutions desirable to materialize
X ≡min Y: X and Y coincide in the minimal instances

55. Minimal knowledge bases as good kb-solutions
What are good knowledge-base solutions?
◮ first choice: universal kb-solutions, but
◮ there are some other kb-solutions desirable to materialize
X ≡min Y: X and Y coincide in the minimal instances
(I2 , Γ2 ) is a minimal kb-solution of (I1 , Γ1 ) under M if
Mod(I2 , Γ2 ) ≡min SolM (Mod(I1 , Γ1 ))
We consider minimal kb-solutions as the good solutions

56. Two requirements to construct
minimal knowledge-base solutions
Given (I1 , Γ1 ) and Σ, when constructing a
minimal-knowledge base solution (I2 , Γ2 ) we would want:
1. Γ2 to only depend on Γ1 and Σ
Γ2 is safe for Γ1 and Σ

57. Two requirements to construct
minimal knowledge-base solutions
Given (I1 , Γ1 ) and Σ, when constructing a
minimal-knowledge base solution (I2 , Γ2 ) we would want:
1. Γ2 to only depend on Γ1 and Σ
Γ2 is safe for Γ1 and Σ
Definition
Γ2 is safe for Γ1 and Σ, if for every I1 there exists I2 s.t.
(I2 , Γ2 ) is a minimal kb-solution of (I1 , Γ1 )

58. Two requirements to construct
minimal knowledge-base solutions
Given (I1 , Γ1 ) and Σ, when constructing a
minimal-knowledge base solution (I2 , Γ2 ) we would want:
2. Γ2 to be as informative as possible
thus minimizing the size of I2

59. Two requirements to construct
minimal knowledge-base solutions
Given (I1 , Γ1 ) and Σ, when constructing a
minimal-knowledge base solution (I2 , Γ2 ) we would want:
2. Γ2 to be as informative as possible
thus minimizing the size of I2
Γ2 is optimum-safe if for every other safe set Γ′
Γ2 |= Γ′

60. Safe sets: data independent target knowledge bases
Unfortunately, optimum-safe sets are not (always) FO-expressible
Theorem
There exist sets Γ1 (full & acyclic) and Σ (full) s.t.
no FO sentence is optimum-safe for Γ1 and Σ

61. Safe sets: data independent target knowledge bases
Unfortunately, optimum-safe sets are not (always) FO-expressible
Theorem
There exist sets Γ1 (full & acyclic) and Σ (full) s.t.
no FO sentence is optimum-safe for Γ1 and Σ
In our paper:
An algorithm to compute optimum-safe set in SO

62. Safe sets: data independent target knowledge bases
Unfortunately, optimum-safe sets are not (always) FO-expressible
Theorem
There exist sets Γ1 (full & acyclic) and Σ (full) s.t.
no FO sentence is optimum-safe for Γ1 and Σ
In our paper:
An algorithm to compute optimum-safe set in SO
Can we do better? not optimum but useful set?
(non-trivial safe set in a good language)

63. We can compute a good safe set
for acyclic tgds knowledge bases
Input: Γ1 acyclic full-tgds, Σ full-tgds (from S to T)

64. We can compute a good safe set
for acyclic tgds knowledge bases
Input: Γ1 acyclic full-tgds, Σ full-tgds (from S to T)
1. Unfold Γ1 to get Γ+
1

65. We can compute a good safe set
for acyclic tgds knowledge bases
Input: Γ1 acyclic full-tgds, Σ full-tgds (from S to T)
1. Unfold Γ1 to get Γ+
1
2. Construct Σ− (from T to S) as follows:
for every α(¯ ) → R(¯) in Γ+
x x 1

66. We can compute a good safe set
for acyclic tgds knowledge bases
Input: Γ1 acyclic full-tgds, Σ full-tgds (from S to T)
1. Unfold Γ1 to get Γ+
1
2. Construct Σ− (from T to S) as follows:
for every α(¯ ) → R(¯) in Γ+
x x 1
Rewrite α(¯) in the target of Σ to obtain β(¯ )
x x

67. We can compute a good safe set
for acyclic tgds knowledge bases
Input: Γ1 acyclic full-tgds, Σ full-tgds (from S to T)
1. Unfold Γ1 to get Γ+
1
2. Construct Σ− (from T to S) as follows:
for every α(¯ ) → R(¯) in Γ+
x x 1
Rewrite α(¯) in the target of Σ to obtain β(¯ )
x x
Add β(¯) → R(¯) to Σ−
x x

68. We can compute a good safe set
for acyclic tgds knowledge bases
Input: Γ1 acyclic full-tgds, Σ full-tgds (from S to T)
1. Unfold Γ1 to get Γ+
1
2. Construct Σ− (from T to S) as follows:
for every α(¯ ) → R(¯) in Γ+
x x 1
Rewrite α(¯) in the target of Σ to obtain β(¯ )
x x
Add β(¯) → R(¯) to Σ−
x x
3. Let Γ2 = Σ− ◦ Σ

69. We can compute a good safe set
for acyclic tgds knowledge bases
Input: Γ1 acyclic full-tgds, Σ full-tgds (from S to T)
1. Unfold Γ1 to get Γ+
1
2. Construct Σ− (from T to S) as follows:
for every α(¯ ) → R(¯) in Γ+
x x 1
Rewrite α(¯) in the target of Σ to obtain β(¯ )
x x
Add β(¯) → R(¯) to Σ−
x x
3. Let Γ2 = Σ− ◦ Σ
Theorem
Γ2 is safe for Γ1 and Σ
(Γ2 is a set of full-tgds with =)

70. In the paper: a complete strategy for computing
minimal knowledge-base solutions
Given Γ1 and Σ:
◮ We compute Γ2 safe for Γ1 and Σ
◮ We then compute minimal set Γ∗ (implied by Γ1 ) such that
for every I1

71. In the paper: a complete strategy for computing
minimal knowledge-base solutions
Given Γ1 and Σ:
◮ We compute Γ2 safe for Γ1 and Σ
◮ We then compute minimal set Γ∗ (implied by Γ1 ) such that
for every I1
chaseΓ∗ (I1 )

72. In the paper: a complete strategy for computing
minimal knowledge-base solutions
Given Γ1 and Σ:
◮ We compute Γ2 safe for Γ1 and Σ
◮ We then compute minimal set Γ∗ (implied by Γ1 ) such that
for every I1
chaseΣ ( chaseΓ∗ (I1 ))

73. In the paper: a complete strategy for computing
minimal knowledge-base solutions
Given Γ1 and Σ:
◮ We compute Γ2 safe for Γ1 and Σ
◮ We then compute minimal set Γ∗ (implied by Γ1 ) such that
for every I1
chaseΣ ( chaseΓ∗ (I1 )), Γ2

74. In the paper: a complete strategy for computing
minimal knowledge-base solutions
Given Γ1 and Σ:
◮ We compute Γ2 safe for Γ1 and Σ
◮ We then compute minimal set Γ∗ (implied by Γ1 ) such that
for every I1
chaseΣ ( chaseΓ∗ (I1 )), Γ2
is a minimal kb-solution for (I1 , Γ1 ).

75. Outline
Formalism for exchanging representations systems
Applications to incomplete instances
Applications to knowledge bases
What is the complexity of testing kb-solutions?
How can we compute a good kb-solution?
Concluding remarks

76. We can exchange more than complete data
We propose a general formalism
to exchange representation systems
◮ Applications to incomplete instances
◮ Applications to knowledge bases

77. We can exchange more than complete data
We propose a general formalism
to exchange representation systems
◮ Applications to incomplete instances
◮ Applications to knowledge bases
Next step: apply our general setting to the Semantic Web
◮ Semantic Web data have nulls (blank nodes)
◮ Semantic Web specifications have rules (RDFS, OWL)

78. Exchanging More than Complete Data
Jorge P´rez
e
Universidad de Chile
joint work with Marcelo Arenas (PUC-Chile) and Juan Reutter (Univ. Edinburgh)

79. Outline
Formalism for exchanging representations systems
Applications to incomplete instances
Applications to knowledge bases
What is the complexity of testing kb-solutions?
How can we compute a good kb-solution?
Concluding remarks