Download to read offline
アンケートデータ集計・分析のためのExcel
- 1.
- 2. はじめに：分析ツールインストール ファイル→オプション →アドイン 左下の管理（A） Excelアドインを選んで設 定をクリック 分析ツールをチェックし てOKをクリック
- 3. 分析ツールで出来ること（一部） 相関・共分散の計算 回帰分析 ヒストグラム作成 統計的検定 平均の差の検定：t検定，ｚ検定 分散分析：一元配置、二元配置 F検定
- 4. 分析ツールの使い方 データ→データ分析 をクリック ヒストグラムを選択 他の分析も同じ方法で選 択
- 5.
- 6.
- 7. ヒストグラムの作り方（２） データ→データ分析 →分析ツール→ヒストグラ ム 入力するもの 入力範囲：グラフにするデー タ データ区間：目盛り 出力先：1セルだけ指定する と、そこから結果が出力され る
- 8. ヒストグラムの作り方（３） 右のような結果が出る これをグラフ化すれば OK データ区間頻度 5 0 10 3 15 4 20 5 25 3 30 5 35 4 40 3 45 2 次の級 0
- 9.
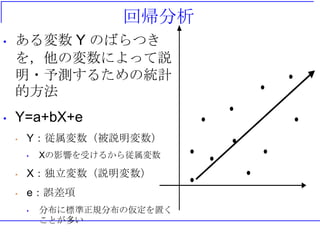
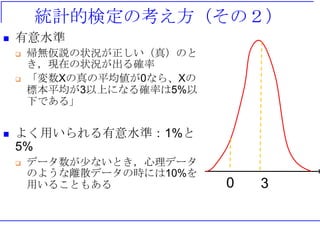
- 10. 回帰分析 • ある変数 Yのばらつき を，他の変数によって説 明・予測するための統計 的方法 • Y=a+bX+e • Y：従属変数（被説明変数） • Xの影響を受けるから従属変数 • X：独立変数（説明変数） • e：誤差項 • 分布に標準正規分布の仮定を置く ことが多い
- 11. 重回帰分析 複数の要素による関数で 回帰させる Y=a+b1X1+b2X2+…+Xn+e 考え方 基本的に1変数の回帰と同じ 影響する変数が複数になっ ただけ 多重共線性に注意 よく似た変数を複数入れて はいけない 理由1 理由2 理由3 理由4 理由5 結 果
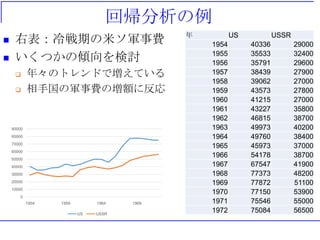
- 12. 回帰分析の例 右表：冷戦期の米ソ軍事費 いくつかの傾向を検討 年々のトレンドで増えている 相手国の軍事費の増額に反応 年 US USSR 1954 40336 29000 1955 35533 32400 1956 35791 29600 1957 38439 27900 1958 39062 27000 1959 43573 27800 1960 41215 27000 1961 43227 35800 1962 46815 38700 1963 49973 40200 1964 49760 38400 1965 45973 37000 1966 54178 38700 1967 67547 41900 1968 77373 48200 1969 77872 51100 1970 77150 53900 1971 75546 55000 1972 75084 56500 0 10000 20000 30000 40000 50000 60000 70000 80000 90000 1954 1959 1964 1969 US USSR
- 13.
- 14. 回帰分析のやり方（２）分析ツール上 入力元 Y範囲：軍事費 USA，USSR X範囲：TREND ※ラベルをチェックする と， 1文字目は見出し扱い 出力：どこでもOK 残差：必要に応じて
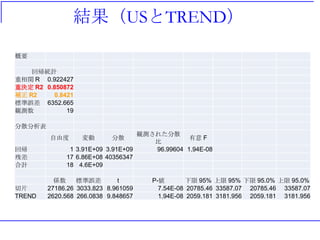
- 15. 結果（USとTREND） 概要 回帰統計 重相関 R 0.922427 重決定R2 0.850872 補正 R2 0.8421 標準誤差 6352.665 観測数 19 分散分析表 自由度 変動 分散 観測された分散 比 有意 F 回帰 1 3.91E+09 3.91E+09 96.99604 1.94E-08 残差 17 6.86E+08 40356347 合計 18 4.6E+09 係数 標準誤差 t P-値 下限 95% 上限 95% 下限 95.0% 上限 95.0% 切片 27186.26 3033.823 8.961059 7.54E-08 20785.46 33587.07 20785.46 33587.07 TREND 2620.568 266.0838 9.848657 1.94E-08 2059.181 3181.956 2059.181 3181.956
- 16. 結果の見方：単回帰 概要 回帰統計 重相関 R 0.922427 重決定R2 0.850872 補正 R2 0.8421 標準誤差 6352.665 観測数 19 分散分析表 自由度 変動 分散 観測された分散 比 有意 F 回帰 1 3.91E+09 3.91E+09 96.99604 1.94E-08 残差 17 6.86E+08 40356347 合計 18 4.6E+09 係数 標準誤差 t P-値 下限 95% 上限 95% 下限 95.0% 上限 95.0% 切片 27186.26 3033.823 8.961059 7.54E-08 20785.46 33587.07 20785.46 33587.07 TREND 2620.568 266.0838 9.848657 1.94E-08 2059.181 3181.956 2059.181 3181.956 回帰モデルの説明力 R-Squared,R2とも言う 下は自由度調整済みR2 F検定の結果（ココでは有意） 回帰モデルそのものの検定 ほとんどの場合で有意 係数の値=0のt検定の結果（ココでは有意） 目安：P値が0.05より小さい（5％有意） ※個別の変数の有意性の検定
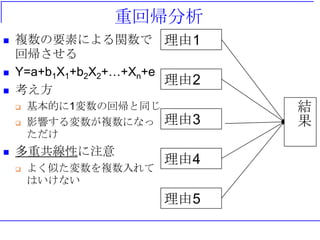
- 17. 結果の見方：重回帰 概要 回帰統計 重相関 R 0.949254 重決定R2 0.901084 補正 R2 0.888719 標準誤差 3342.582 観測数 19 分散分析表 自由度 変動 分散 観測され た分散比 有意 F 回帰 2 1.63E+09 8.14E+08 72.87667 9.17E-09 残差 16 1.79E+08 11172853 合計 18 1.81E+09 係数 標準誤差 t P-値 下限 95% 上限 95% 下限 95.0% 上限 95.0% 切片 12589.56 3818.999 3.296559 0.004552 4493.64 20685.47 4493.64 20685.47 TREND 708.1907 362.5476 1.953373 0.068491 -60.3759 1476.757 -60.3759 1476.757 US 0.357182 0.127615 2.798903 0.01287 0.08665 0.627714 0.08665 0.627714 さっきのモデルとの比較では 補正R2を見る。 今回は増えてるのでこちらの方が説明力は高いが・・・ USSRをTRENDとUSで 回帰したケース TRENDが5％水準でも有意ではない そのため、このモデルはそのままでは あまりよろしくない
- 18. 結果の書き方（単回帰／重回帰共通） 回帰分析の結果を論文に書くときの例 US=27186.3+2620.6TREND (8.97**) (9.85**) F=0.00**，修正R2=0.84 *は5％水準，**は1%水準で有意 小数第2位か3位で四捨五入 必要な項目 切片と各変数の係数の推計値 上に対応する各推計値のt値＆それぞれが有意かどうか F値＆有意かどうか，修正R2の値
- 19. 参考：多重共線性 Multicollinearity（通称マルチコ） 変数の変動パターンがほぼ同じ（相関が強い）2 組以上の変数が回帰式にある状態．これがあると， 結果は信用できない． VIF（Variance Inflation Factor）など，判定基準がある 要するに・・・ Y=a+b1X1+b2X2+…+Xn+e でX1とX2が完全に同じなら， b1とb2の値は全く信用できない 同じでなくても，相関が高いとまずいことはわかりますよね？ 実際の調査でやりそうな例だと・・・ 勤続年数と年齢，勤続年数と収入
- 20.
- 21. 統計的検定の考え方（その１） 例：変数Xの標本平均が3となった →これが単なる偶然でなく，0より大きいことを 統計的に示したい 帰無仮説：「こうあってほしくない」仮説 論破するために立てる仮説 例の事例だと： 「変数Xの真の平均値は0である」 棄却域：帰無仮説が正しくない、とする確率の範 囲
- 22. 統計的検定の考え方（その２） 有意水準 帰無仮説の状況が正しい（真）のと き，現在の状況が出る確率 「変数Xの真の平均値が0なら、Xの 標本平均が3以上になる確率は5%以 下である」 よく用いられる有意水準：1%と 5% データ数が少ないとき，心理データ のような離散データの時には10%を 用いることもある 30
- 23. 回帰式の結果の見方 1. F検定の結果を見る これが有意でないと、回帰式自体の意味がない 2.各回帰変数のｔ検定の結果を見る 変数の係数（β）の真の値がゼロである，の検定です t値の大きさで判定：経験上は3以上 t検定に通っていない変数は，説明力がない，とみな す 3. 決定係数(R-Squared，R2)を見る 定義：（モデルで説明できた変動）÷（全変動） 値が大きいほど，データの変動を説明できた度合いが大きい 自由度修正済み決定係数側を見ることが多い 経済系：0.9ぐらい普通，心理系：0.3程度はほしい
- 24. 回帰分析・重回帰分析でわかること • ある変数が別の変数に影響を与えているかを知る ことが出来る • 「Xが～増えたら、Yが・・・増える」と言った、 予想に用いることが出来る •複数の変数があるとき、どの変数の影響が大きい かを知ることが出来る
- 25.
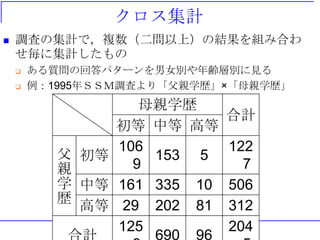
- 26. フェイスと単純集計 フェイスシート 回答者の個人的な属性を聞いている部分 性別，年齢，家族構成，収入，社会的地位．．． 心理的・社会的傾向でない質問部分 回答傾向に影響が与えることが多いため，クロス集計 で用いる 単純集計 質問項目をそのまま集計したもの 0% 20% 40% 60% 80% 100% 男性ラノベ 女性ラノベ 一般小説 ラノベ雑誌 文芸誌 ケータイ小説 全くない 年に数回 月に１回 週に１回 週に複数
- 27. 単純集計で使う関数：COUNTIF関数 範囲内で条件を満たす セルの個数を返す関数 書式 COUNTIF(範囲，条件） 条件を満たすセルの個数が 返される 条件が等式：値そのまま 不等式：条件を” ”で囲む COUNTIF(A1:A10,”>20”) 右：フェイスデータ（一部） F1-1（年齢）に，18と回答した人数を計算して いる 27
- 28. クロス集計 調査の集計で，複数（二問以上）の結果を組み合わ せ毎に集計したもの ある質問の回答パターンを男女別や年齢層別に見る 例：1995年ＳＳＭ調査より「父親学歴」×「母親学歴」 母親学歴 合計 初等 中等 高等 父 親 学 歴 初等 106 9 153 5 122 7 中等 161 335 10 506 高等 29 202 81 312 125 690 96 204
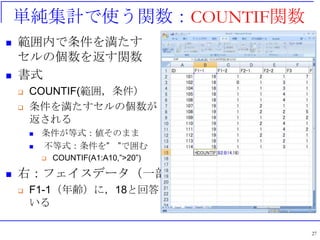
- 29. クロス集計で使う関数：COUNTIFS関 数 範囲内で条件を満たすセルの個数を返す関数 Countif関数と混同しないように 書式 COUNTIFS(範囲，条件,範囲，条件, …） 範囲・条件のペア数：クロスさせる項目の数と同じ 条件を満たすセルの個数が返される 条件が等式：値そのまま（文字の場合は“”で囲む） 不等式：条件を” ”で囲む 性別・学科別人数の計算例 COUNTIFS($C$3:$C$83,1,$E$3:$E$83,1) 赤文字部分：1つめの範囲と条件 青文字部分：2つめの範囲と条件 COUNTIFS関数1つで1つの項目 クロス集計の項目数と同じ数だけ，条件の値を変えて繰り返す データに例があるので，詳細はそちらを参照すること
- 30. 相関とは 定義 他の条件を同じにして，ある変数（属性）だけを変化 させる 別のある変数の（集計）結果が変化するとき，これを 相関が存在するという 相関関係＝因果関係とは限らない 相関は因果の必要条件だが，十分条件ではない クロス集計の例だと・・・ 父親学歴と母親学歴に高い相関 厳密には，結婚時期や年齢などもコントロールすべき
- 31. 変数間の関係を表す統計量 共分散と相関係数 共 分散 xy i iin i iin syx YYXXYXCov 1 1 ))((),( 相 関 係 数 yx xy ss s YVarXVar YXCov r )()( ),(
- 32. 相関関係と因果関係（１） ある変数Aと別の変数Bの間に相関が見られたとき， 以下のような可能性がある 1. 調査法に問題がある（サンプルが偏っている） 2.AがBの直接的な原因：A→B 3. BがAの直接的な原因：B→A 4. AとBが相互に影響を与えている：A⇔B 5. AがBの間接原因である A→未知変数C→B Aと相関関係にある未知変数C→B A→未知変数C，Cと相関関係にある未知変数D→B 出典：谷岡（2007）
- 33. 相関関係と因果関係（２） ある変数Aと別の変数Bの間に相関が見られたとき， 以下のような可能性がある（続） 6. AもBも第3の未知変数Cの結果 C→AおよびC→Bという結果があったため，AとBに相 関関係が見られた 7. 上記の要因が複合的に関連したもの 8. 単なる偶然 時間的なトレンドを持つデータ同士の相関は簡単に出 る 出典：谷岡（2007）