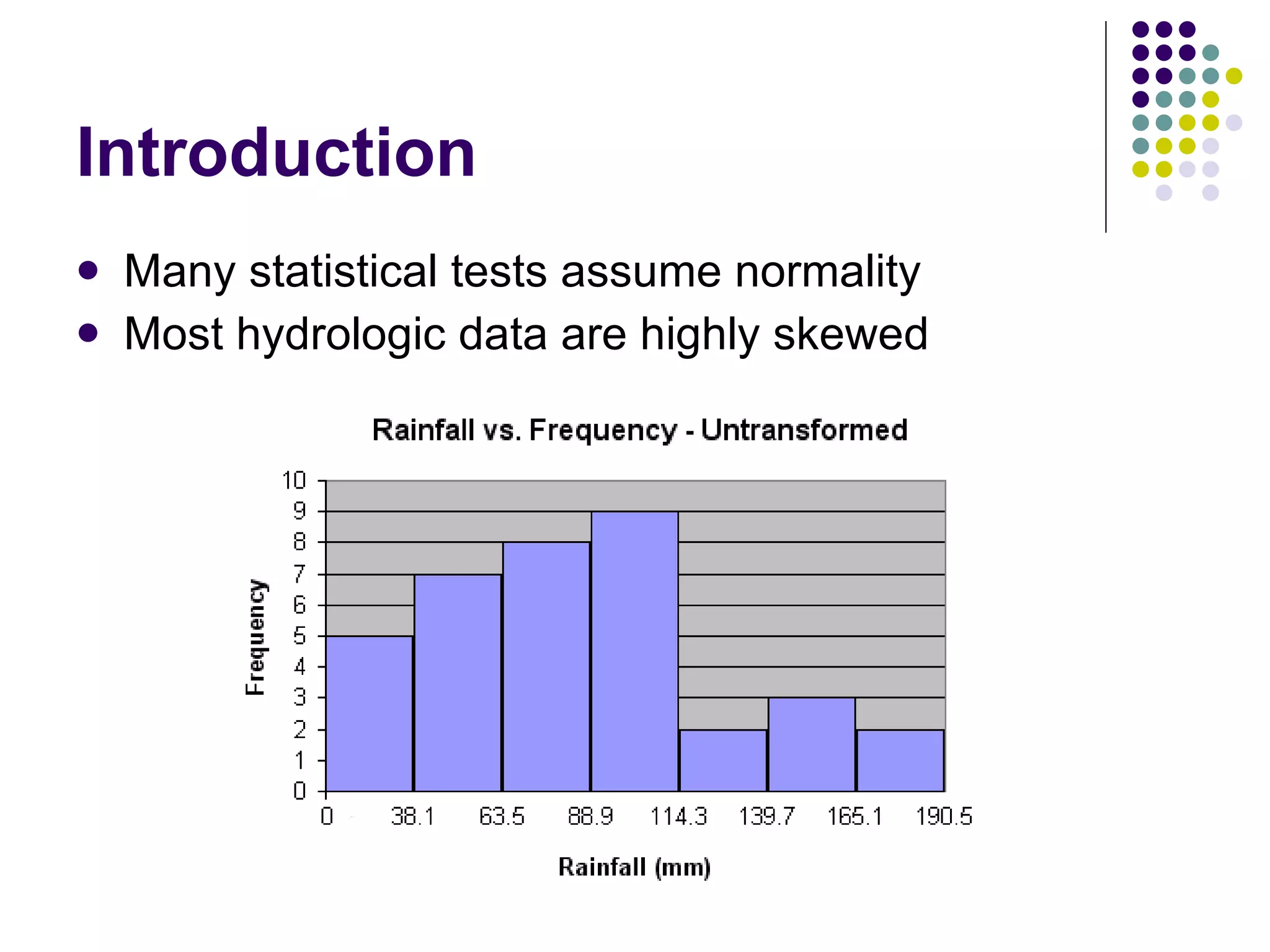
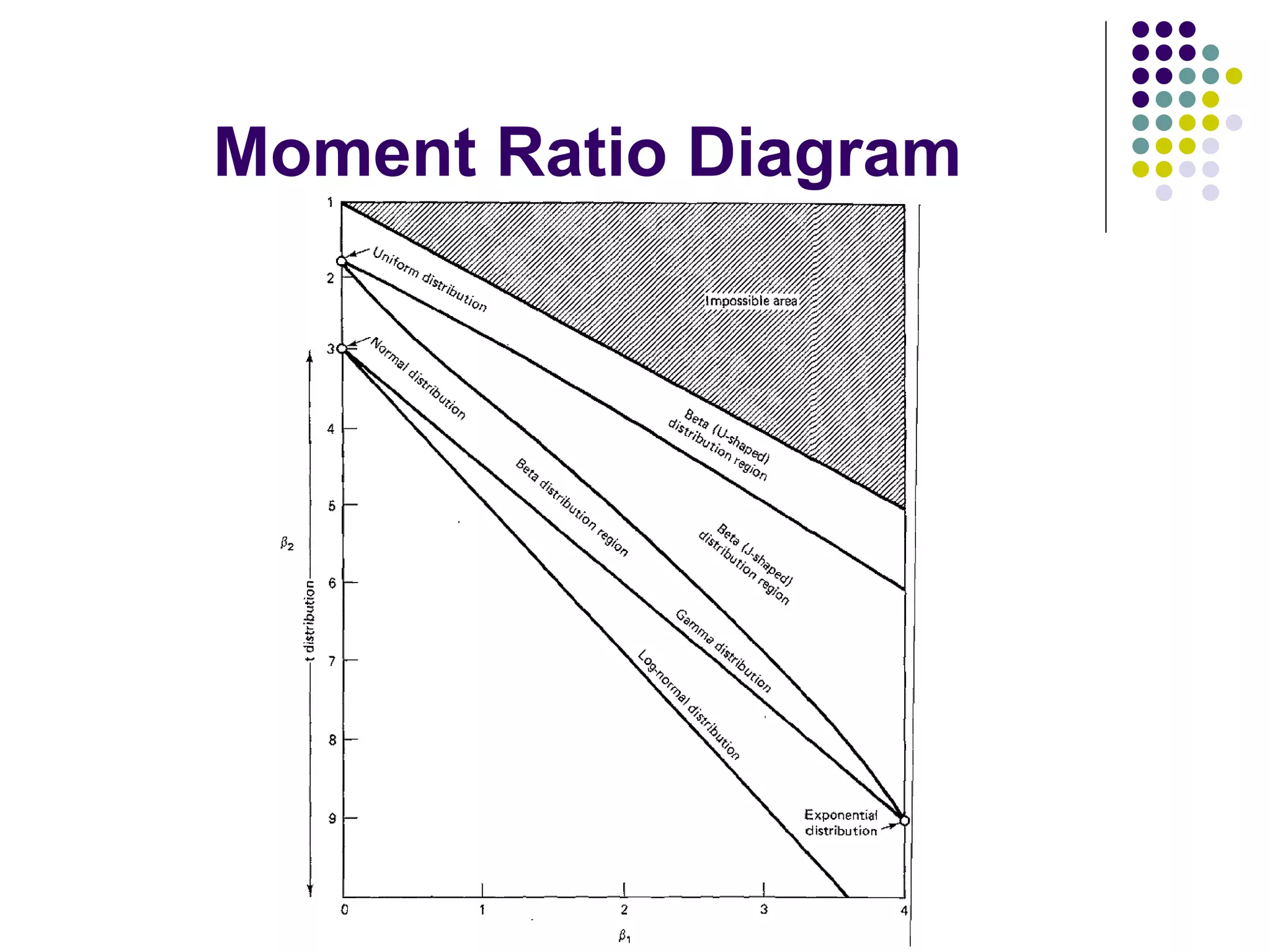
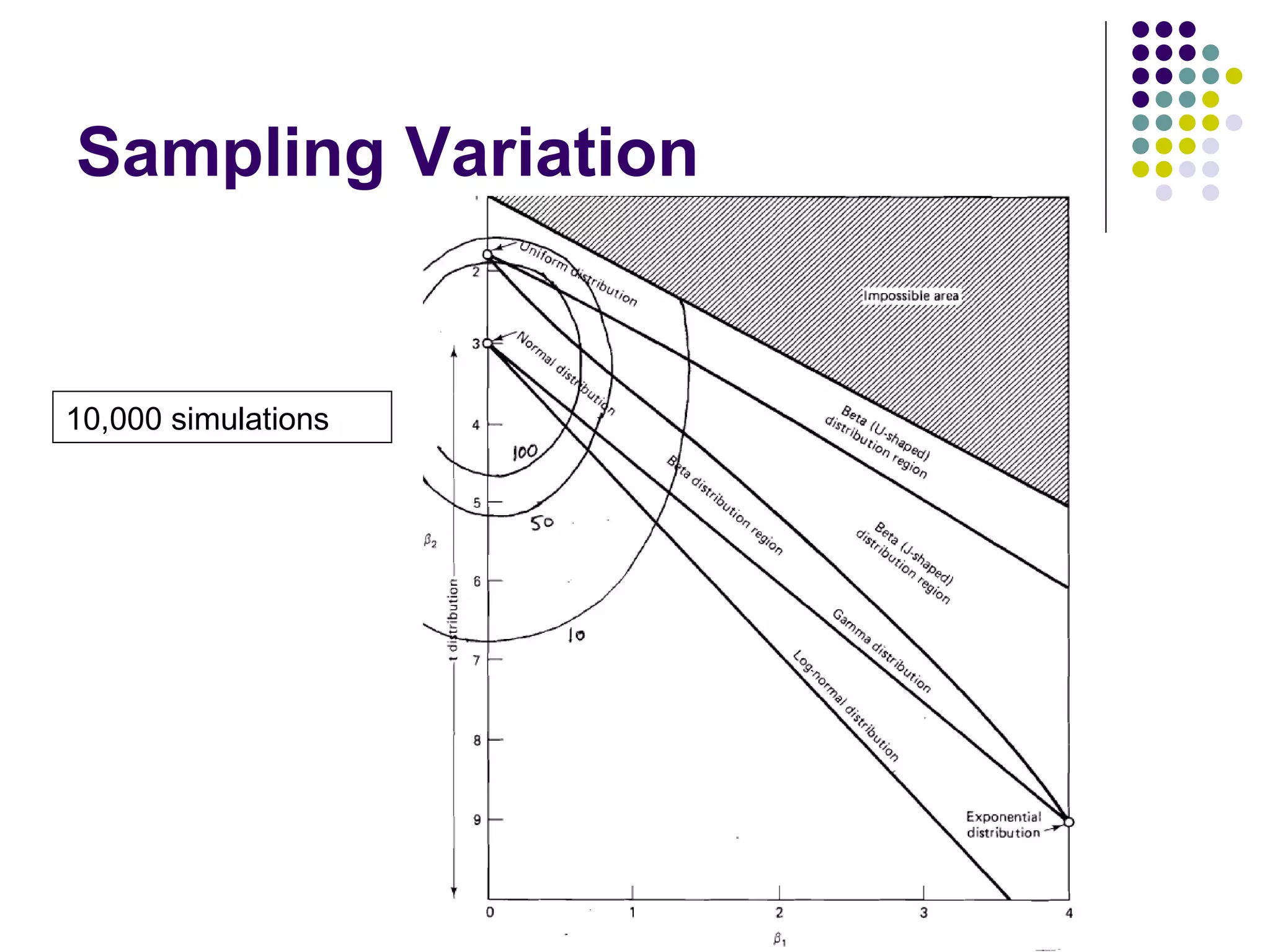
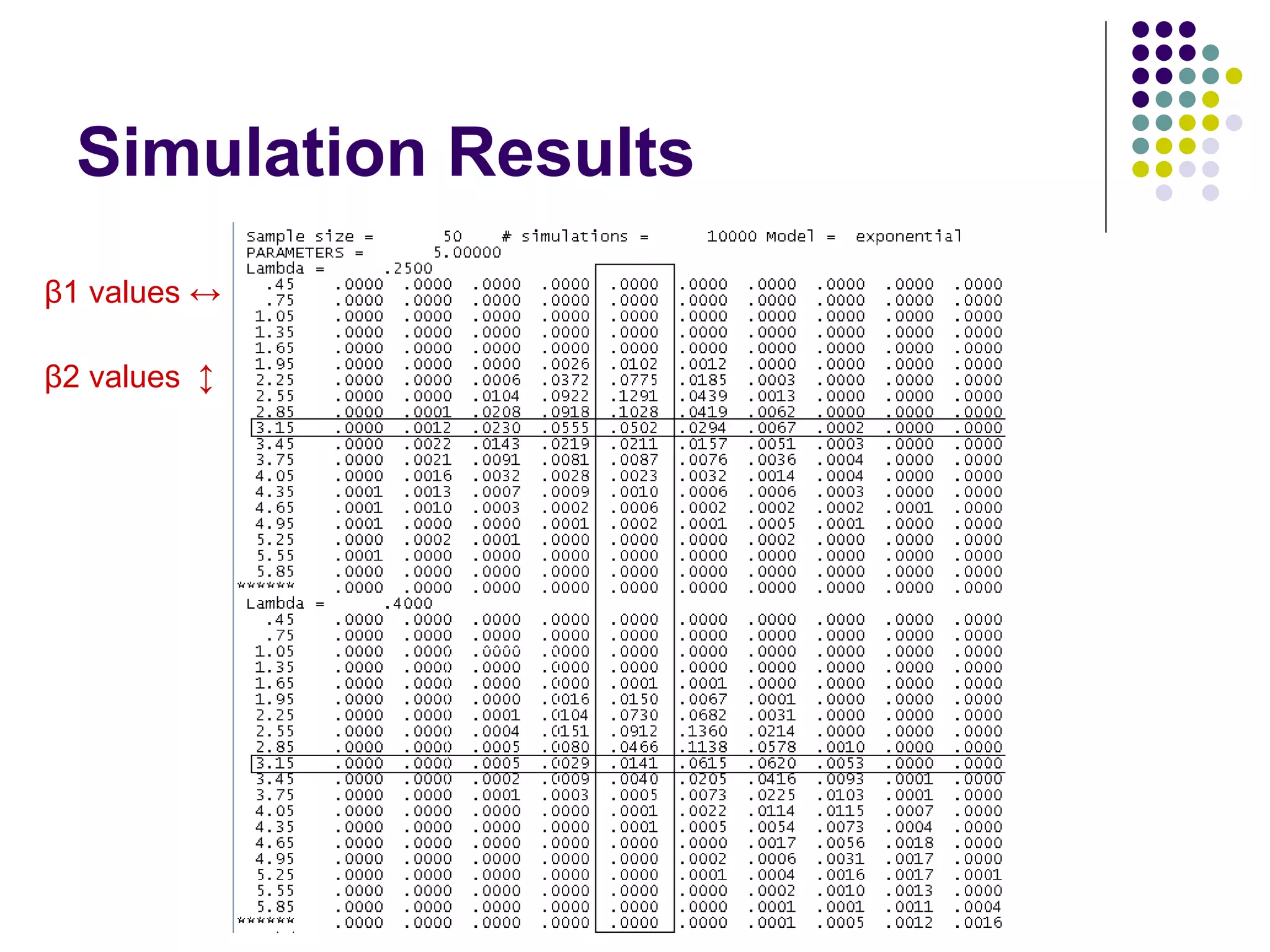
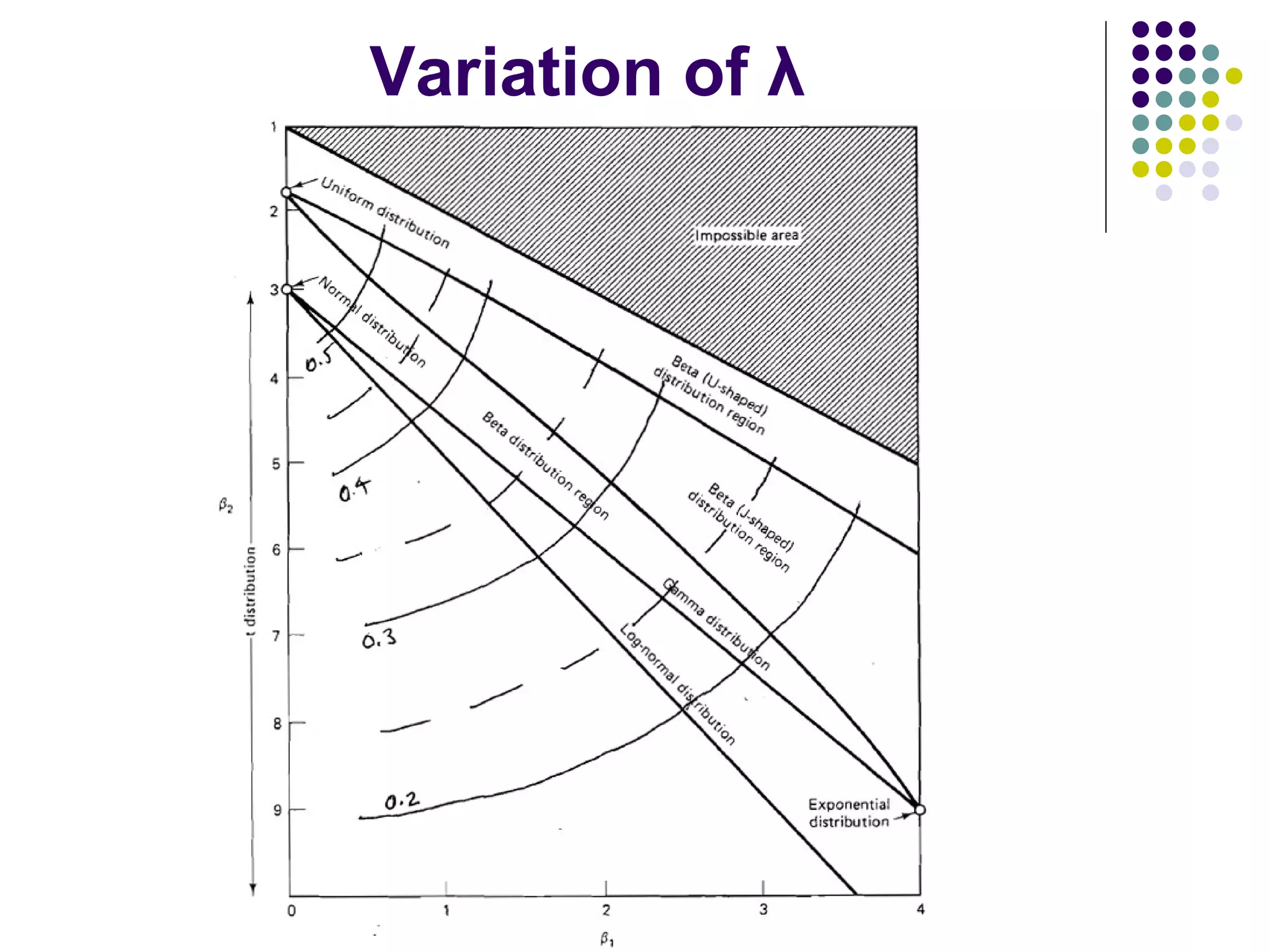
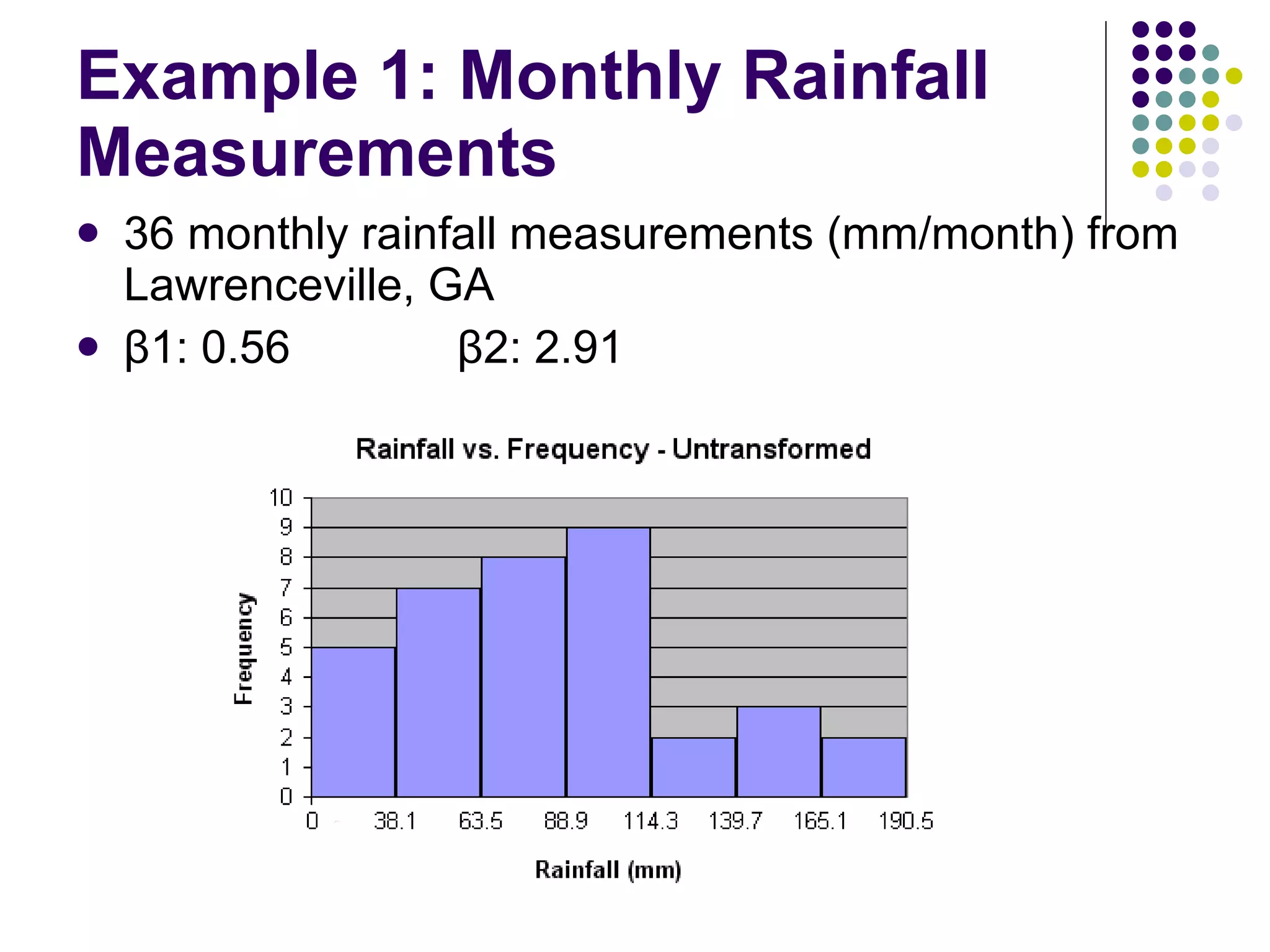
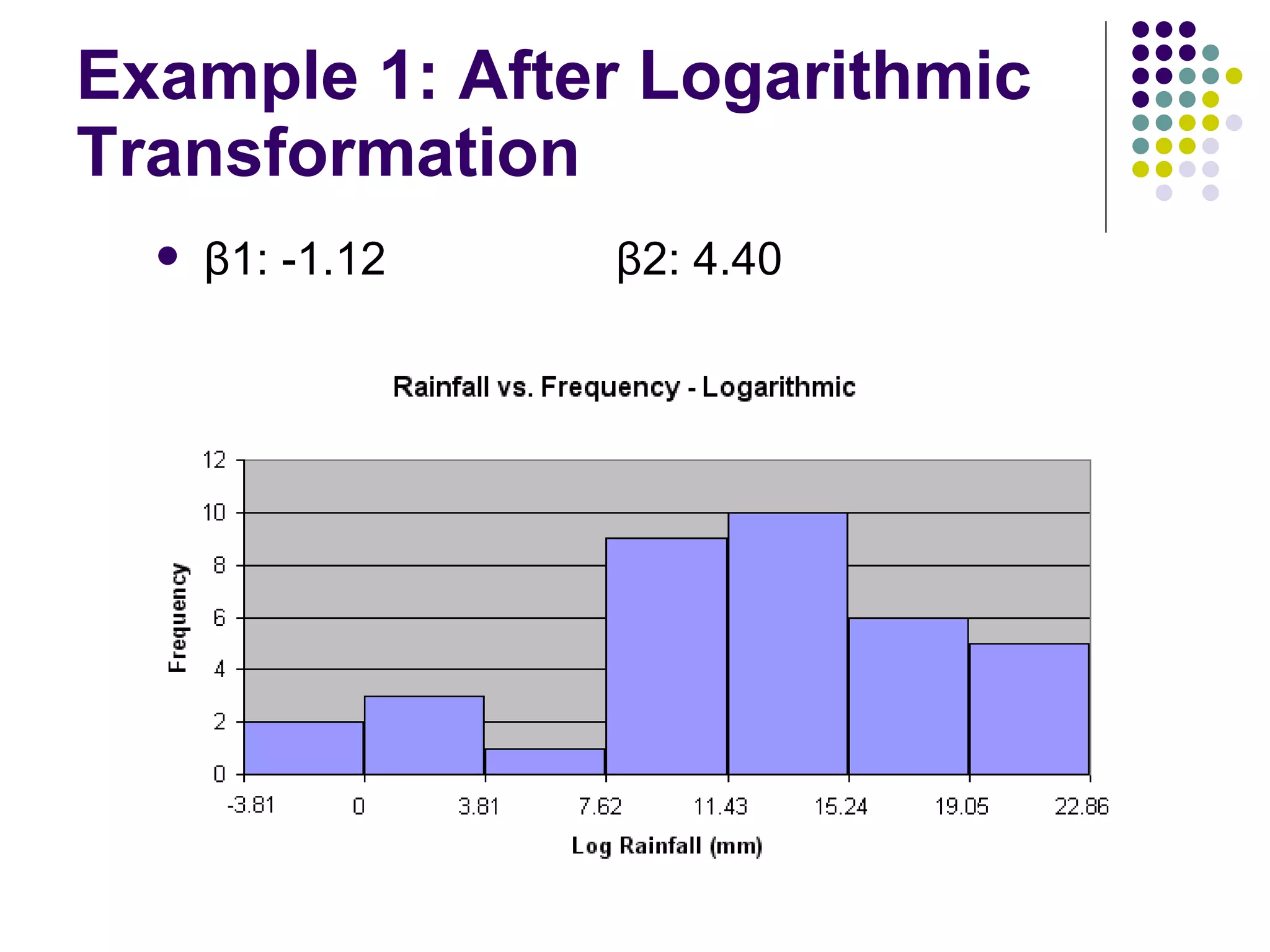
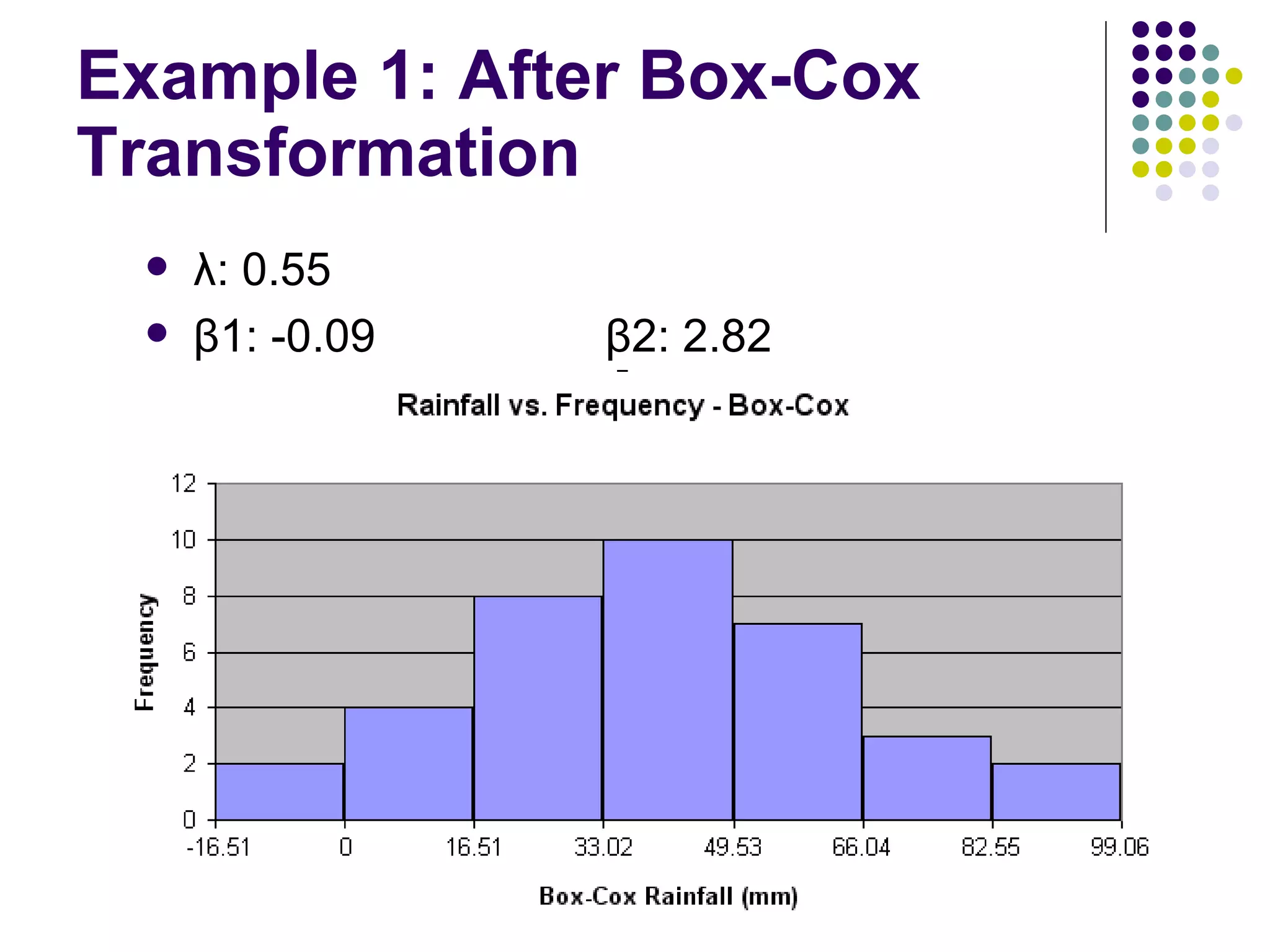
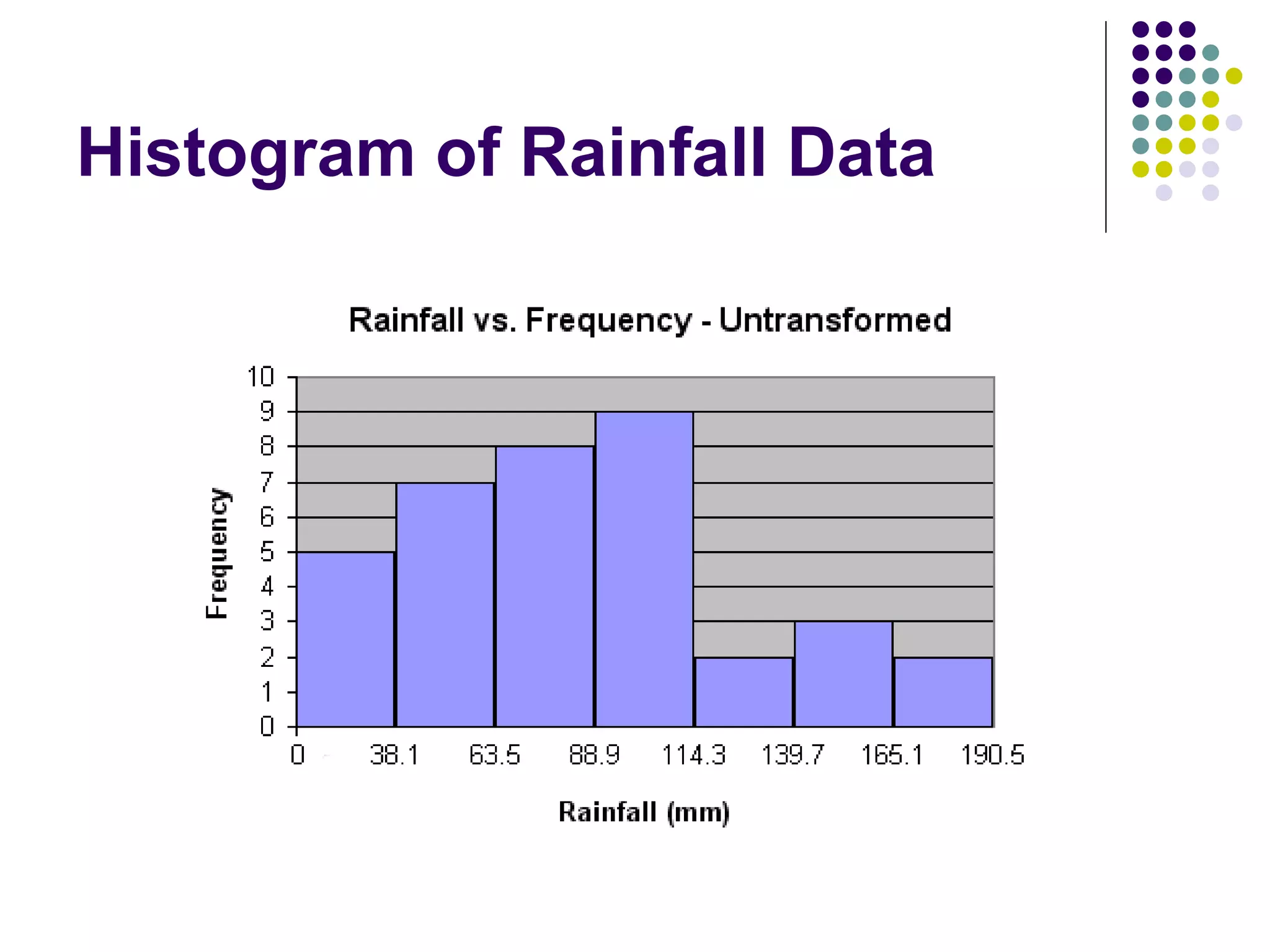
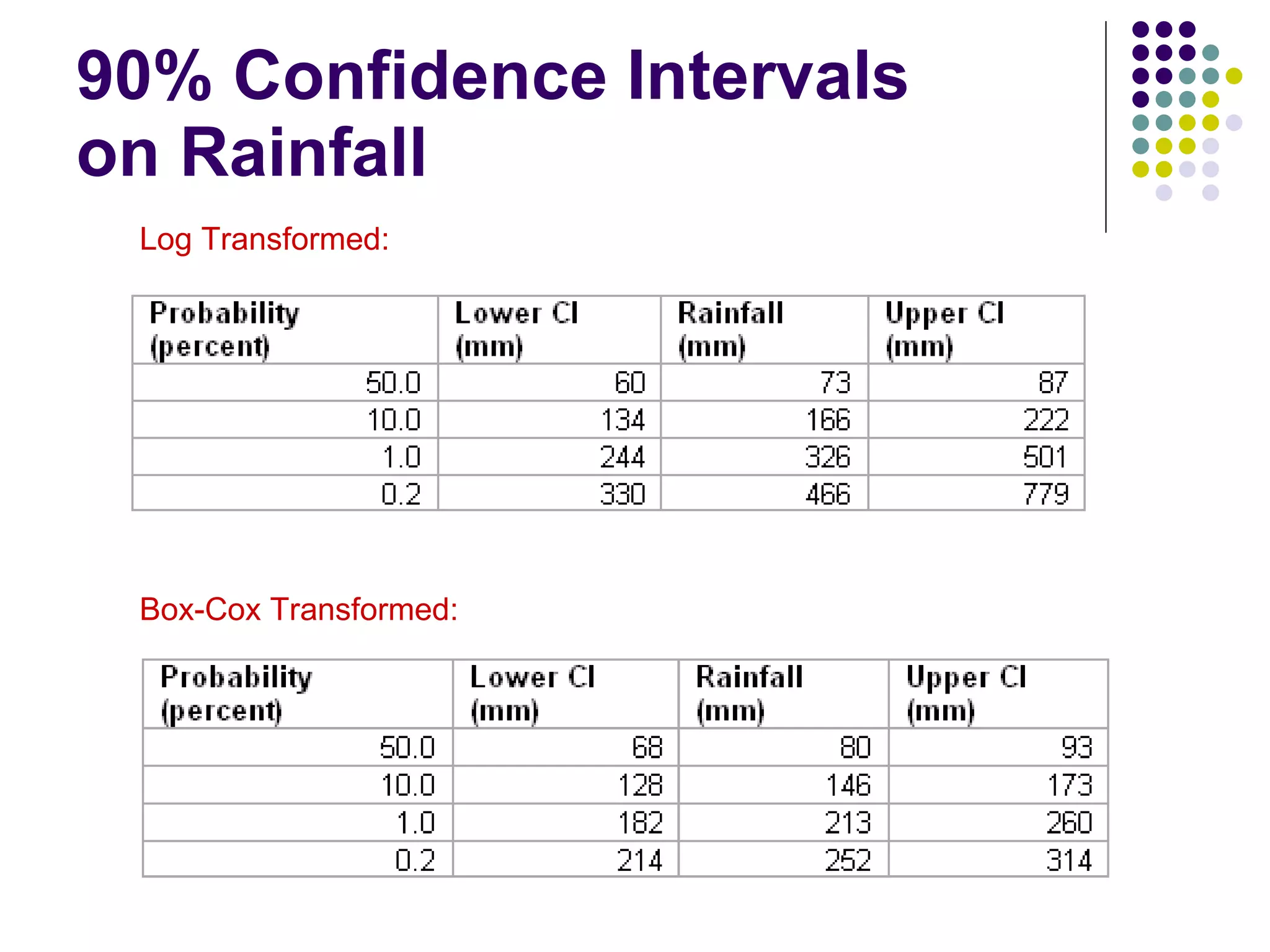
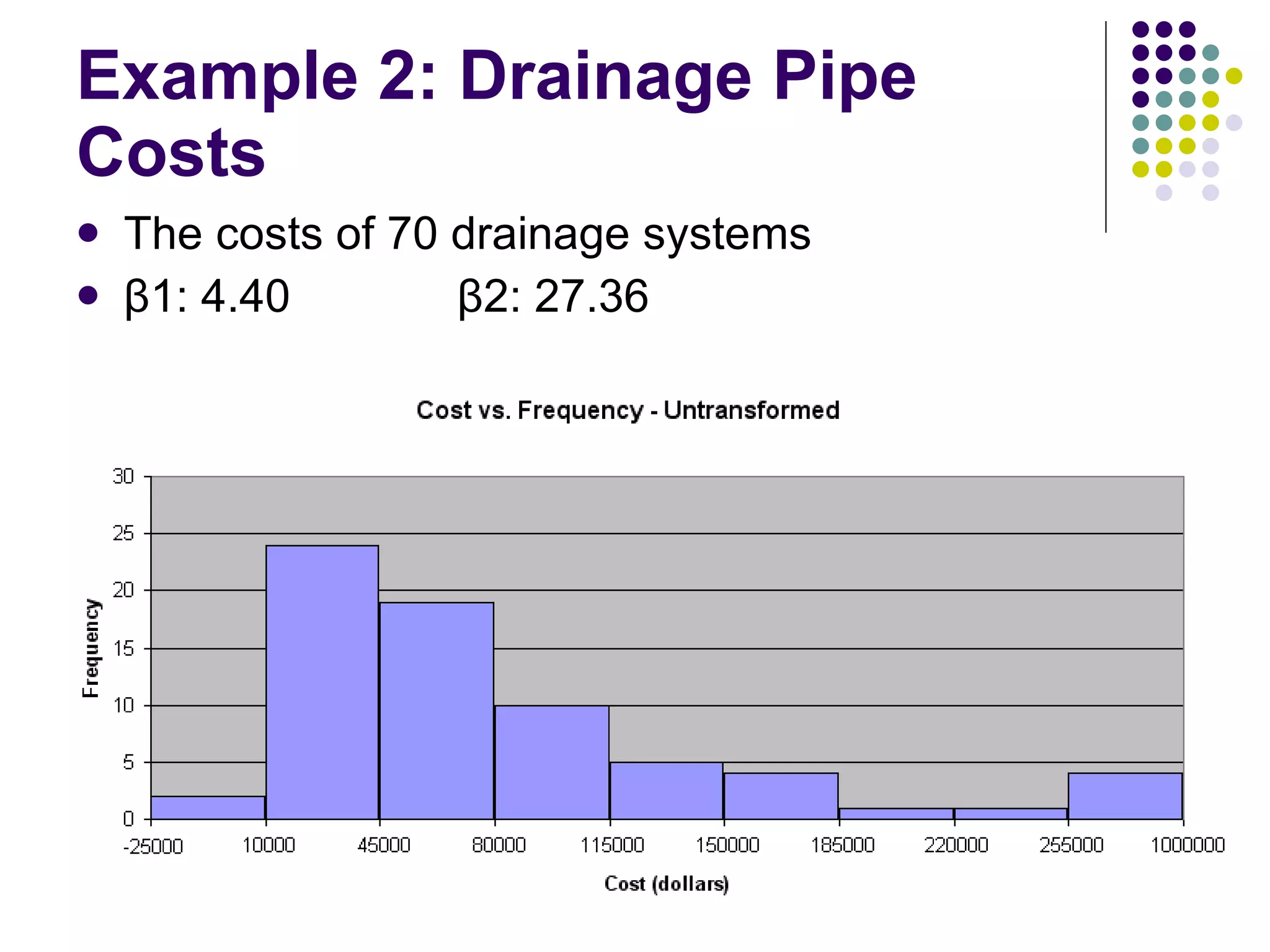
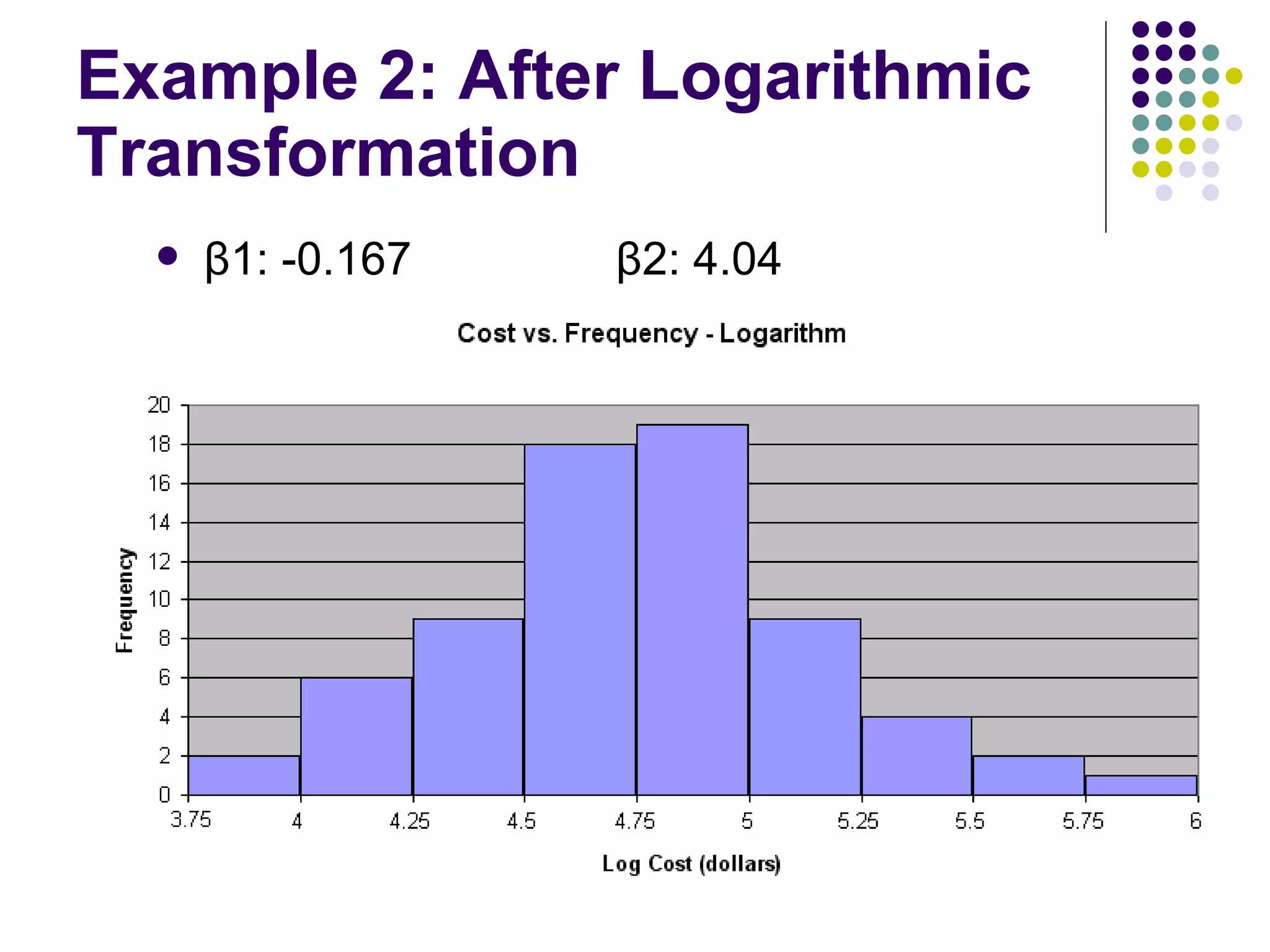
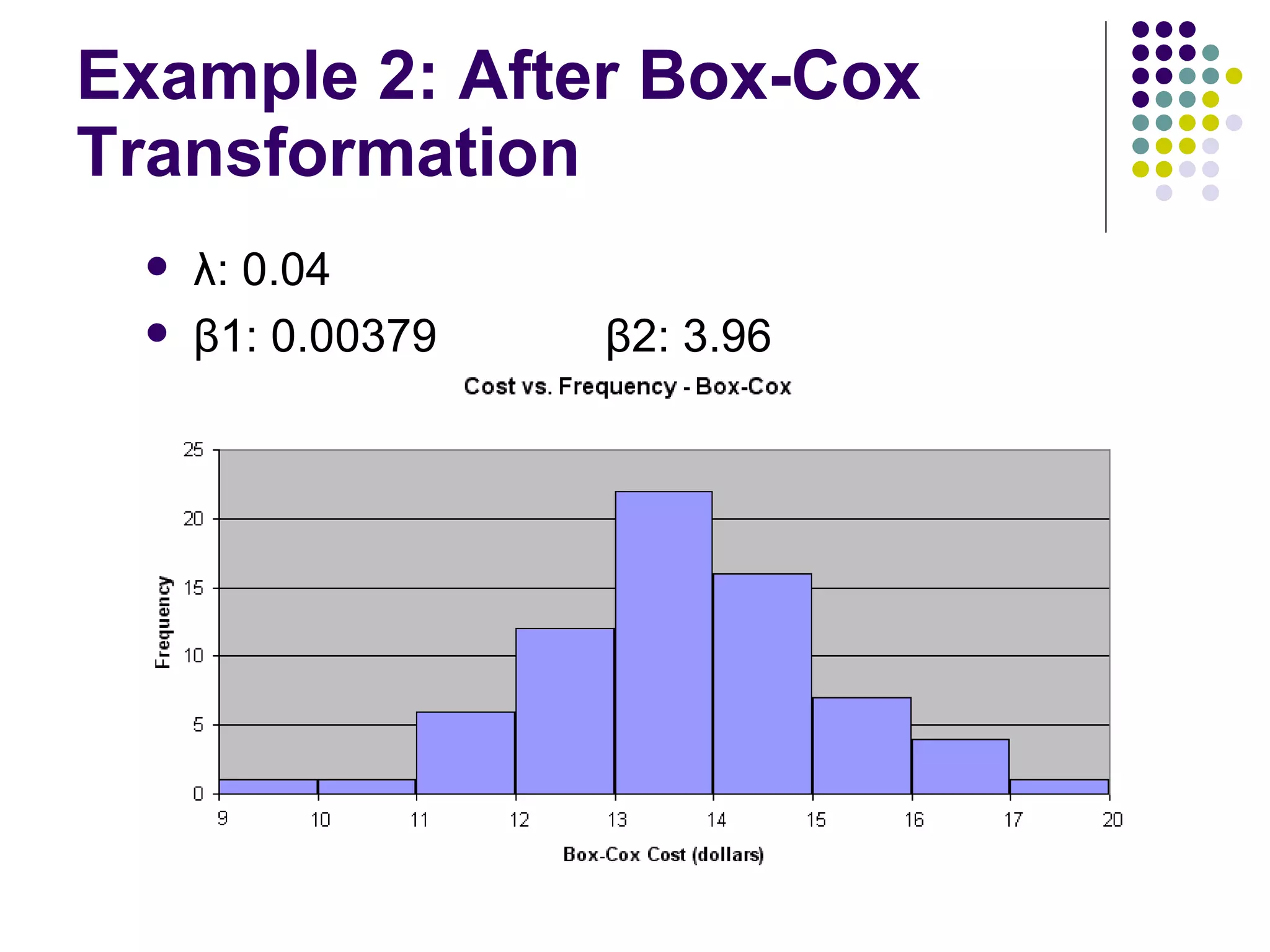
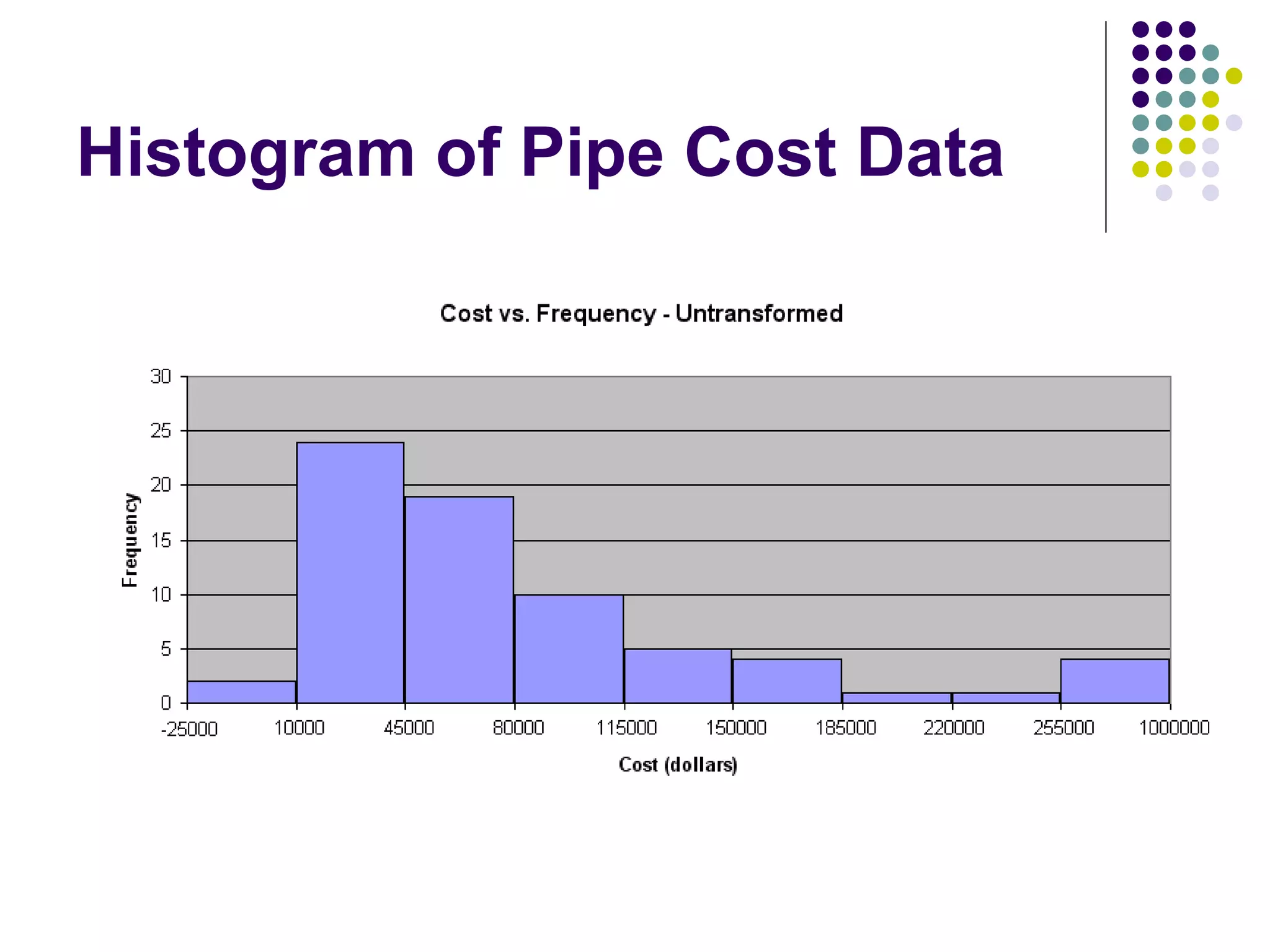
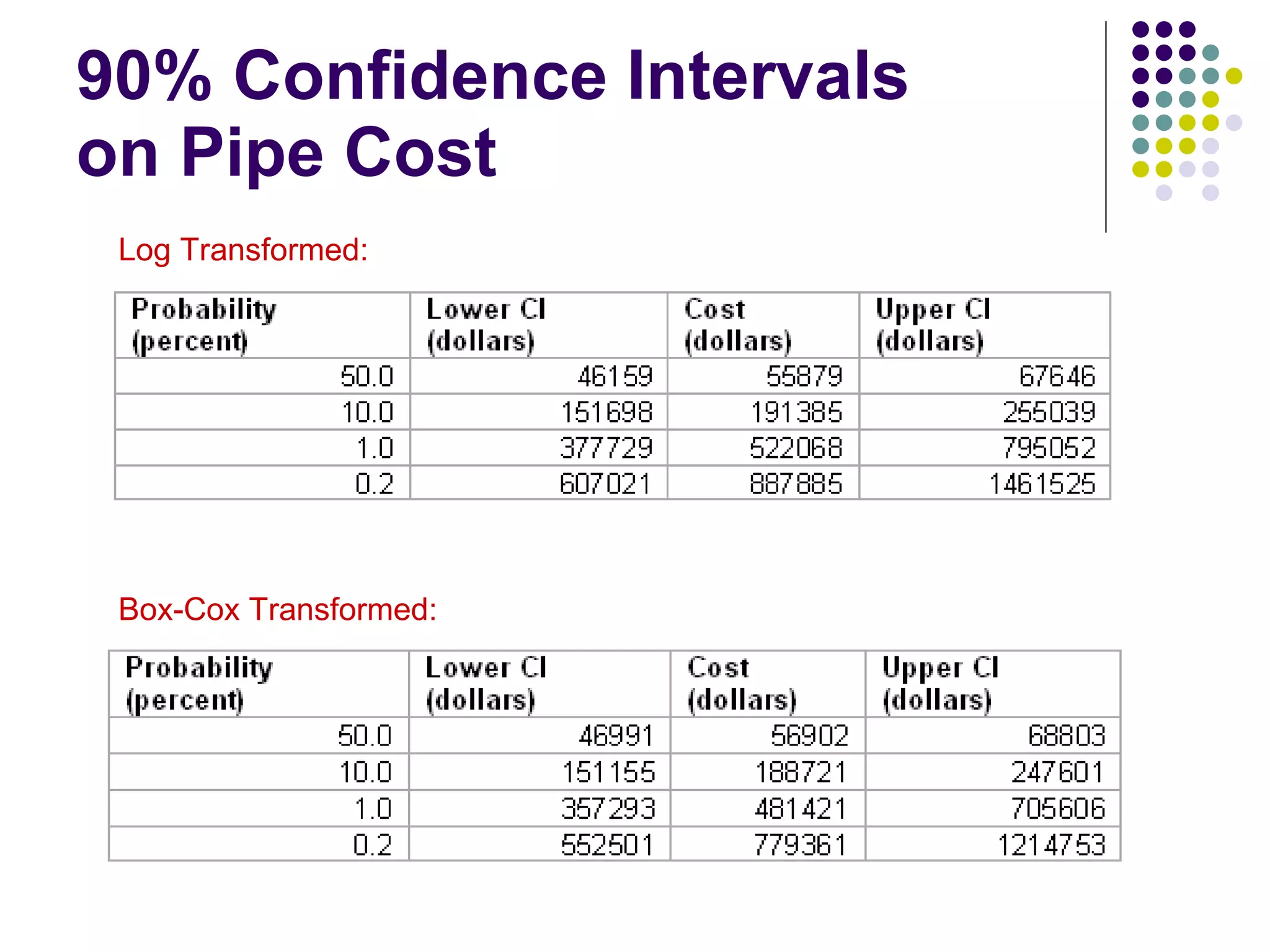
This document discusses methods for normalizing skewed hydrologic data using the Box-Cox transformation. It finds that the Box-Cox transformation provides a better normalization than the logarithmic transformation. Through simulations, it determines the sampling distributions of the Box-Cox parameter λ and how λ relates to measures of skewness and kurtosis. It then demonstrates applying the Box-Cox transformation and confidence intervals to examples of rainfall and drainage pipe cost data.

1. Estimation of the Box-Cox Transformation Parameter and Application to Hydrologic Data Melanie Wong Friday, August 29, 2008

2. Introduction Many statistical tests assume normality Most hydrologic data are highly skewed

3. Detecting Normality β1 (third moment) = skewness β2 (fourth moment) = kurtosis Characteristics of a normal distribution: β1=0 β2=3

4. Moment Ratio Diagram

5. Transformation to Normality Hydrologic data are not normal Various transformations available Logarithmic Box-Cox

6. The Box-Cox Transformation

7. Transformation Procedure Decide if sample data is normal Obtain value of λ Transform the data Apply confidence intervals, statistical tests, or tolerance limits Perform inverse transformation

8. Determining the Optimal λ “ Snap-to-the-grid” method Box and Cox (1967): “... fix one, or possibly a small number, of λ's and go ahead with the detailed estimation...” Distribution-based method λ=-1.0 reciprocal transform λ=-0.5 reciprocal square root transform λ=0 natural log transform λ=+0.5 square root transform λ=1.0 no transformation needed

9. Research Goal and Objectives Goal: To develop a better understanding of the Box-Cox transformation so that it can be applied with greater confidence Objectives: To characterize the sampling variation To provide a method for estimating the Box-Cox transformation parameter for any set of data

10. Sampling Variation 10,000 simulations

11. Second Objective To provide a method for estimating the Box-Cox transformation parameter for any set of data

12. The Importance of λ Small changes in λ  Large changes in sampling variation Need a more precise method to obtain optimum λ

13. Optimizing λ Procedure: Monte Carlo simulation to identify sampling distributions of β1 and β2 values for different λ values Distribution types: Gamma, exponential, uniform Population sizes: 1000, 500, 200, 100, 50, 10

14. Simulation Results β1 values ↔ β2 values ↕

15. Variation of λ

16. Confidence Intervals Procedure: Logarithmic 1) Make Logarithmic transformation of x 2) Use normal theory for confidence intervals on y 3) Inverse transform the confidence intervals to values of x

17. Confidence Interval Procedure: Box-Cox 1) Make BCT of x to y using optimum λ 2) Use normal theory for confidence intervals on y 3) Inverse transform the confidence intervals to values of x

18. Example 1: Monthly Rainfall Measurements 36 monthly rainfall measurements (mm/month) from Lawrenceville, GA β1: 0.56 β2: 2.91

19. Example 1: After Logarithmic Transformation β1: -1.12 β2: 4.40

20. Example 1: After Box-Cox Transformation λ: 0.55 β1: -0.09 β2: 2.82

21. Histogram of Rainfall Data

22. 90% Confidence Intervals on Rainfall Box-Cox Transformed: Log Transformed:

23. Example 2: Drainage Pipe Costs The costs of 70 drainage systems β1: 4.40 β2: 27.36

24. Example 2: After Logarithmic Transformation β1: -0.167 β2: 4.04

25. Example 2: After Box-Cox Transformation λ: 0.04 β1: 0.00379 β2: 3.96

26. Histogram of Pipe Cost Data

27. 90% Confidence Intervals on Pipe Cost Box-Cox Transformed: Log Transformed:

28. Conclusions Box-Cox transform is more suitable than logarithmic transform for: Normalizing data Determining confidence intervals, tolerance limits, outliers, and other tests Sampling distributions of λ were determined Optimum values of λ vs. β1 and β2 were developed

29. QUESTIONS?