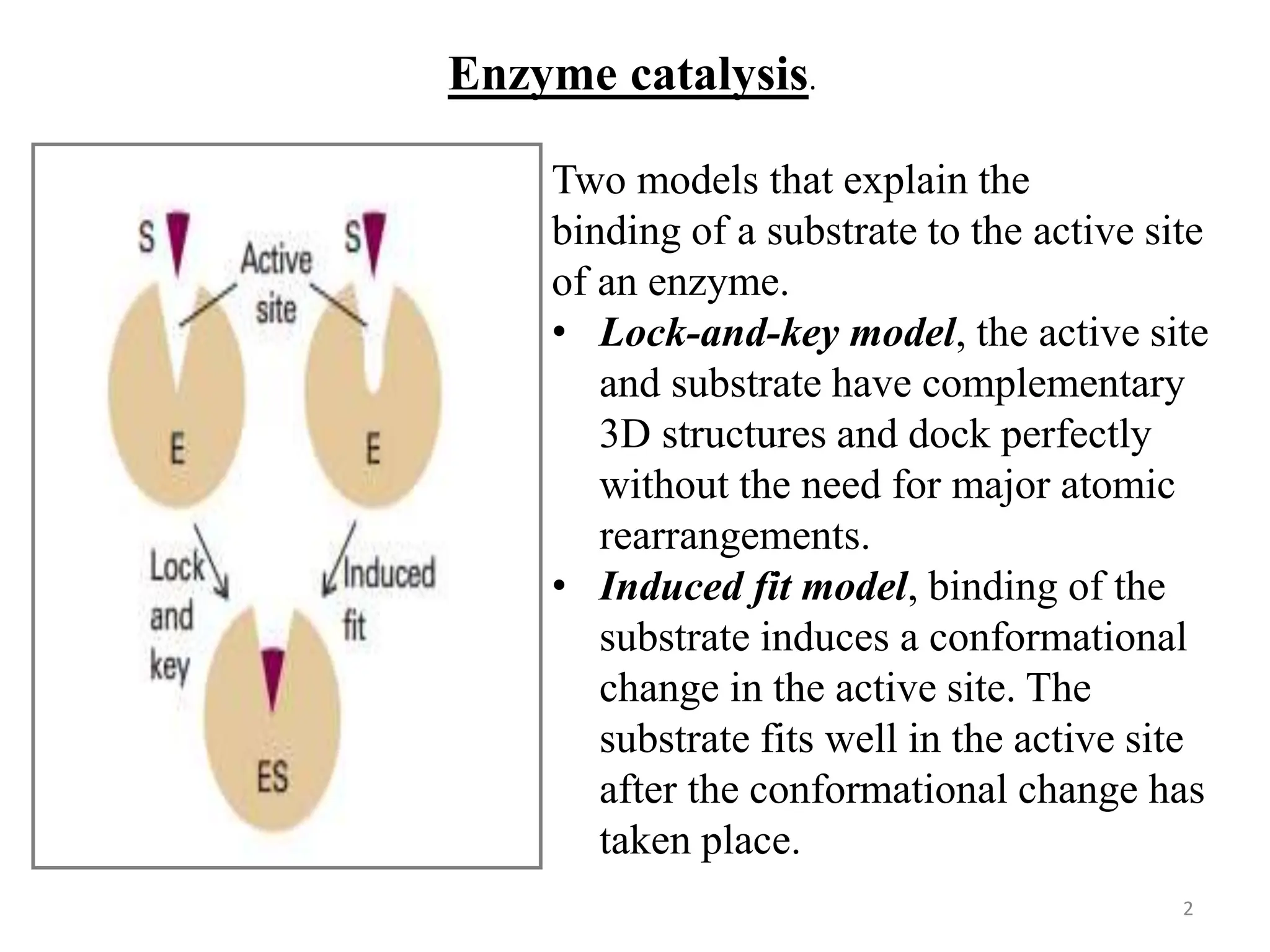
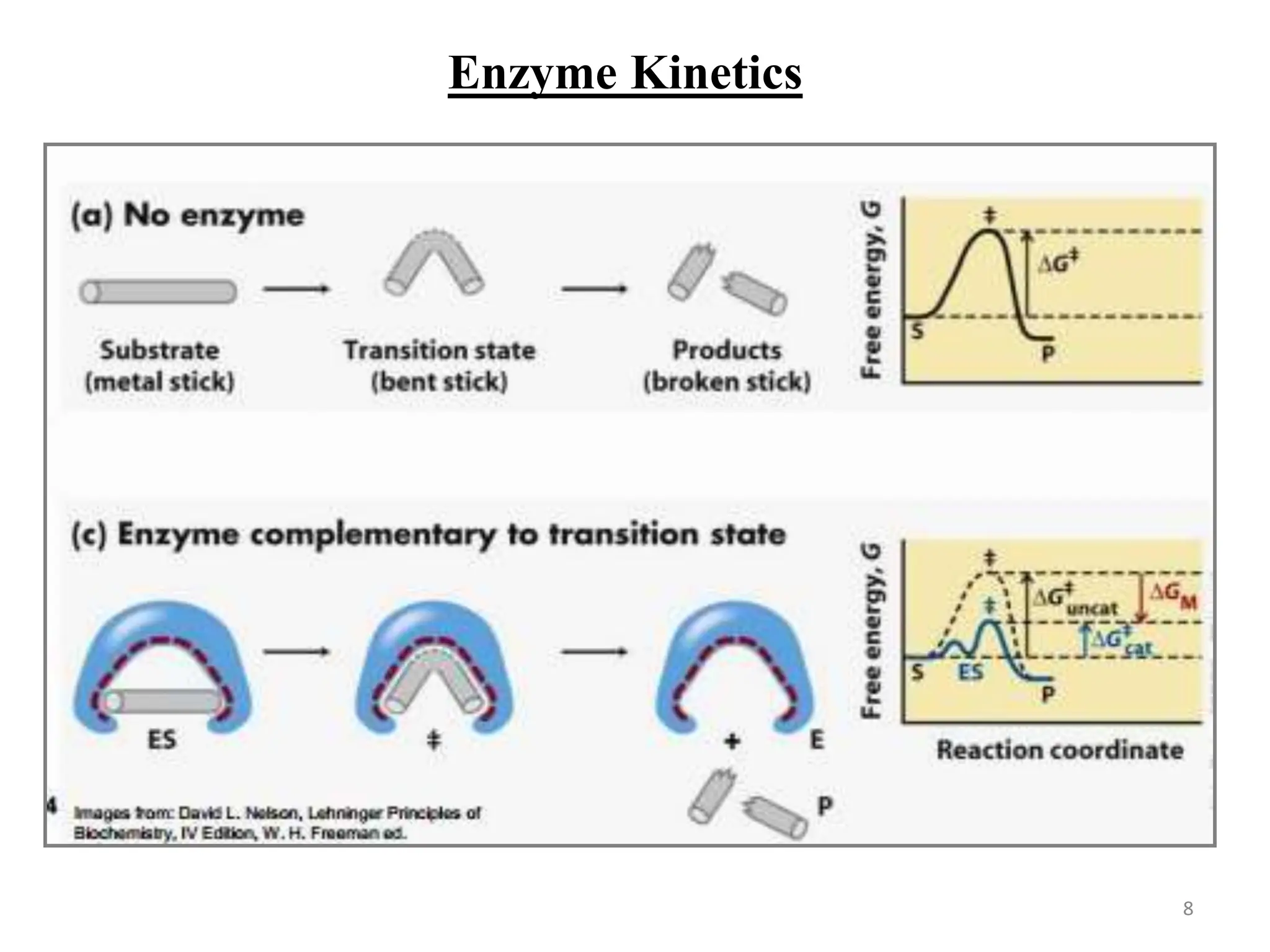
The document discusses enzyme catalysis, highlighting enzymes as biological catalysts with active sites that bind substrates and convert them into products. It elaborates on models that describe substrate binding, such as the lock-and-key and induced fit models, and explains the Michaelis-Menten mechanism for enzyme kinetics. Additionally, it covers the significance of the Michaelis constant (km) and catalytic efficiency (ε), detailing how they relate to enzyme activity and efficiency.

1. 1
Enzyme catalysis.
Enzymes are homogeneous biological catalysts. These ubiquitous
compounds are special proteins or nucleic acids that contain an active
site, which is responsible for binding the substrates, the reactants,
and processing them into products. As is true of any catalyst, the
active site returns to its original state after the products are released.
Many enzymes consist primarily of proteins, some featuring organic
or inorganic co-factors in their active sites. However, certain RNA
molecules can also be biological catalysts, forming ribozymes. A
very important example of a ribozyme is the ribosome, a large
assembly of proteins and catalytically active RNA molecules
responsible for the synthesis of proteins in the cell.

2. 2
Enzyme catalysis.
Two models that explain the
binding of a substrate to the active site
of an enzyme.
• Lock-and-key model, the active site
and substrate have complementary
3D structures and dock perfectly
without the need for major atomic
rearrangements.
• Induced fit model, binding of the
substrate induces a conformational
change in the active site. The
substrate fits well in the active site
after the conformational change has
taken place.

3. 3
• Based on transition state theory, the rate of a reaction is dependent
on the energy difference between the initial state and the highest
energy transient state along the reaction pathway. Thus, rate
enhancements by enzymes must be mediated by a decrease in the
energy of the highest energy transition state.
• A decrease in the energy of the highest energy transition state can
be accomplished;
I. The enzyme stabilizes the transition state. The same transition
II.The enzyme allows a different pathway for the process. In the
enzyme-catalyzed process, the highest energy transition state
(which does not exist in the non-catalyzed process) has a lower
energy than the energy of the transition state for the non-
catalyzed process.
Enzyme Kinetics

4. 4
Consider a reaction in which S is converted to P, either as a simple
chemical reaction or as an enzyme-catalyzed process. Instead of
merely stating S→P, for transition state theory we need to add an
additional term:
In each case, the reaction pathway passes through an identical
transition state, X‡ (in the uncatalyzed pathway, this species is not
bound to the enzyme, but it is the same species in both cases). In
each case in the scheme above, the rate constant shown is the one
for the slowest step in the forward direction reaction.
Enzyme Kinetics

5. 5
Enzyme Kinetics
The energy level diagram below demonstrate the binding of the
substrate and dissociation of the product from the enzyme explicitly.
Note that the ES complex is lower in energy than the free S, which is
why this complex forms spontaneously.
David L. Nelson, Lehninger Principles of Biochemistry, IV Edition, W. H. Freeman ed.

6. 6
Enzyme Kinetics
Using the principles of transition state theory, we can derive an
equation for the rate enhancement mediated by the enzyme.
Note that the rate constant is related to the difference in energy of
between the initial state and the transition state.
Arrhenius equation:
If the rate constant for the catalyzed reaction is divided by that of
the uncatalyzed reaction:
Simplifies to

7. 7
Enzyme Kinetics
At equilibrium Keq and ∆G° are related. Rearranging the standard
equation for ∆G° to solve for Keq, we obtain:
Comparing catalyzed and uncatalyzed Keq,
Thus, the ratio of the rate constant for the catalyzed reaction to that
of the uncatalyzed reaction is equal to the ratio of the equilibrium
constant for the binding of the enzyme to the transition state to that
for the binding to the substrate.

8. 8
Enzyme Kinetics

9. 9
The Michaelis–Menten Mechanism of Enzyme Catalysis
The principal features of many enzyme-catalysed reactions are as
follows:
I. For a given initial concentration of substrate, [S]0, the initial
rate of product formation is proportional to the total
concentration of enzyme, [E]0.
II. For a given [E]0 and low values of [S]0, the rate of product
formation is proportional to [S]0.
III. For a given [E]0 and high values of [S]0, the rate of product
formation becomes independent of [S]0, reaching a maximum
value known as the maximum velocity, vmax

10. 10
The Michaelis–Menten mechanism accounts for these features.
According to this mechanism, an enzyme–substrate complex is
formed in the first step and either the substrate is released
unchanged or after modification to form products:
Consider the following reaction mechanism:
This mechanism leads to the Michaelis– Menten equation for the
rate of product formation;
where Km = (k a′ + kb)/ka is the Michaelis constant, characteristic
of a given enzyme acting on a given substrate.
The Michaelis–Menten Mechanism of Enzyme Catalysis

11. 11
The Michaelis–Menten Mechanism of Enzyme Catalysis
Derivation of Equation:
The rate of product formation according to the Michaelis–Menten
mechanism is:
The concentration of the enzyme–substrate complex is obtained by
invoking the steady-state approximation and writing;
Simplifies to:
where [E] and [S] are the concentrations of free enzyme and
substrate, respectively. Now the Michaelis constant can be defined
as:
KM has the same units as molar concentration

12. 12
The Michaelis–Menten Mechanism of Enzyme Catalysis
To express the rate law in terms of the concentrations of enzyme and
substrate added, we note that: [E]0 =[E] + [ES].
In addition, because the substrate is typically in large excess relative
to the enzyme, the free substrate concentration is approximately equal
to the initial substrate concentration and we can write [S] ≈ [S]0. It
then follows that;
The Michaelis-Menten equation is then obtained by substituting [ES]
is the rate
The Michaelis–Menten Equation

13. 13
Significance of Michaelis–Menten constant, Km
Experimental observation show that:
I. When [S]0 << KM, the rate is proportional to [S]0
II. When [S]0 >> KM, the rate reaches its maximum value and is
independent of [S]0.

14. 14
Significance of Michaelis–Menten constant, Km
Substitution of the definitions of KM and vmax into the Michaelis –
Menten equation;
Rearranging the equation in linear form;
A Lineweaver–Burk plot for the
analysis of an enzyme-catalysed
reaction that proceeds by a
Michaelis–Menten mechanism
and the significance of the
intercepts and the slope.

15. 15
The Catalytic Efficiency of Enzymes
The turnover frequency, or catalytic constant, of an enzyme,
kcat, is the number of catalytic cycles (turnovers) performed by the
active site in a given interval divided by the duration of the
interval.
This quantity has units of a first-order rate constant and,
in terms of the Michaelis–Menten mechanism, is numerically
equivalent to kb, the rate constant for release of product from the
enzyme–substrate complex. It follows from the identification of
kcat with kb and from:
Thus:
# moles (equivalents) reactant (substrate)
# moles (equivalents) catalyst
Turnovers 

16. 16
The Catalytic Efficiency of Enzymes
The catalytic efficiency, ε(epsilon), of an enzyme is the ratio kcat/KM.
The higher the value of ε, the more efficient is the enzyme. We can
think of the catalytic activity as the effective rate constant of the
enzymatic reaction. From KM = (ka′ + kb)/ka and eqn kcat equation, it
follows that;
The efficiency reaches its maximum value of ka when kb >> ka′.
Because ka is the rate constant for the formation of a complex from
two species that are diffusing freely in solution, the maximum
efficiency is related to the maximum rate of diffusion of E and S in
solution.

17. 17
Determining the Catalytic Efficiency of an Enzyme
The enzyme carbonic anhydrase catalyses the hydration of CO2
in red blood cells to give bicarbonate (hydrogen carbonate) ion:
CO2(g) + H2O(l) → HCO3−
(aq) + H+
(aq)
The following data were obtained for the reaction at pH = 7.1,
273.5 K, and an enzyme concentration of 2.3 nmol dm−3
[CO2
]/(mmol dm3
) rate/(mmol dm3
s1
)
1.25 0.0278
2.5 0.05
5 0.0833
20 0.167
Atkins, Physical Chemistry , 8th Ed.

18. 18
Determining the Catalytic Efficiency of an Enzyme
Solution:
Draw a straight line graph to determine KM and Vmax.
[CO2
]/(mmol dm3
) rate/(mmol dm3
s1
) 1/(rate/(mmol dm3
s1
)
1/[CO2
]/(mmol dm3
)
1.25 0.0278 36.0 0.8
2.5 0.05 20.0 0.4
5 0.0833 12.0 0.2
20 0.167 6.0 0.05
Atkins, Physical Chemistry , 8th Ed.

19. 19
Determining the Catalytic Efficiency of an Enzyme...
y = 39.97x + 4.002
R² = 1
0.0
5.0
10.0
15.0
20.0
25.0
30.0
35.0
40.0
0 0.2 0.4 0.6 0.8 1
1/(v/mmol/dm
3
s
1
)
1/(mmol/dm3 [CO2]

20. 20
Determining the Catalytic Efficiency of an Enzyme...
Atkins, Physical Chemistry , 8th Ed.