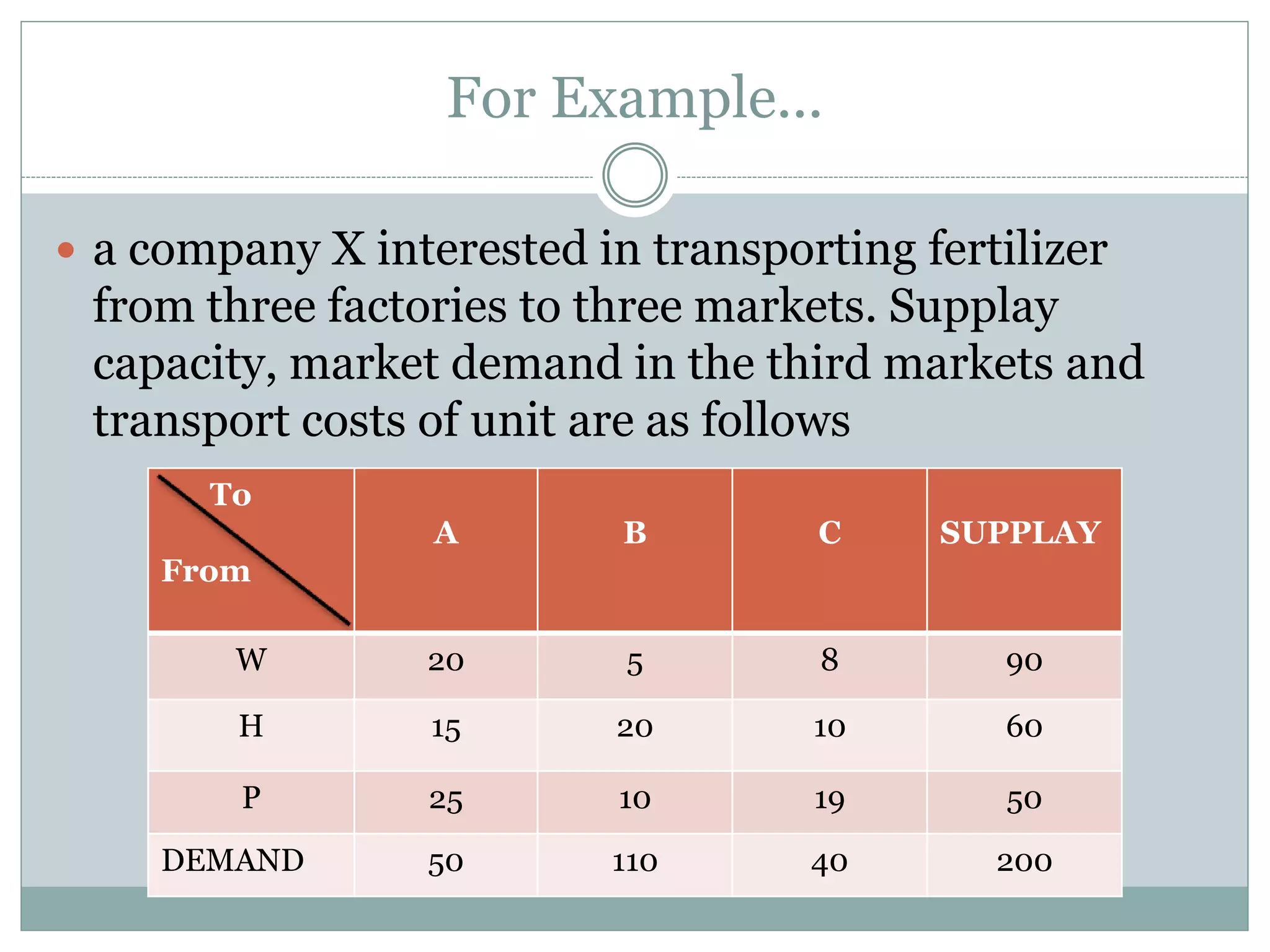
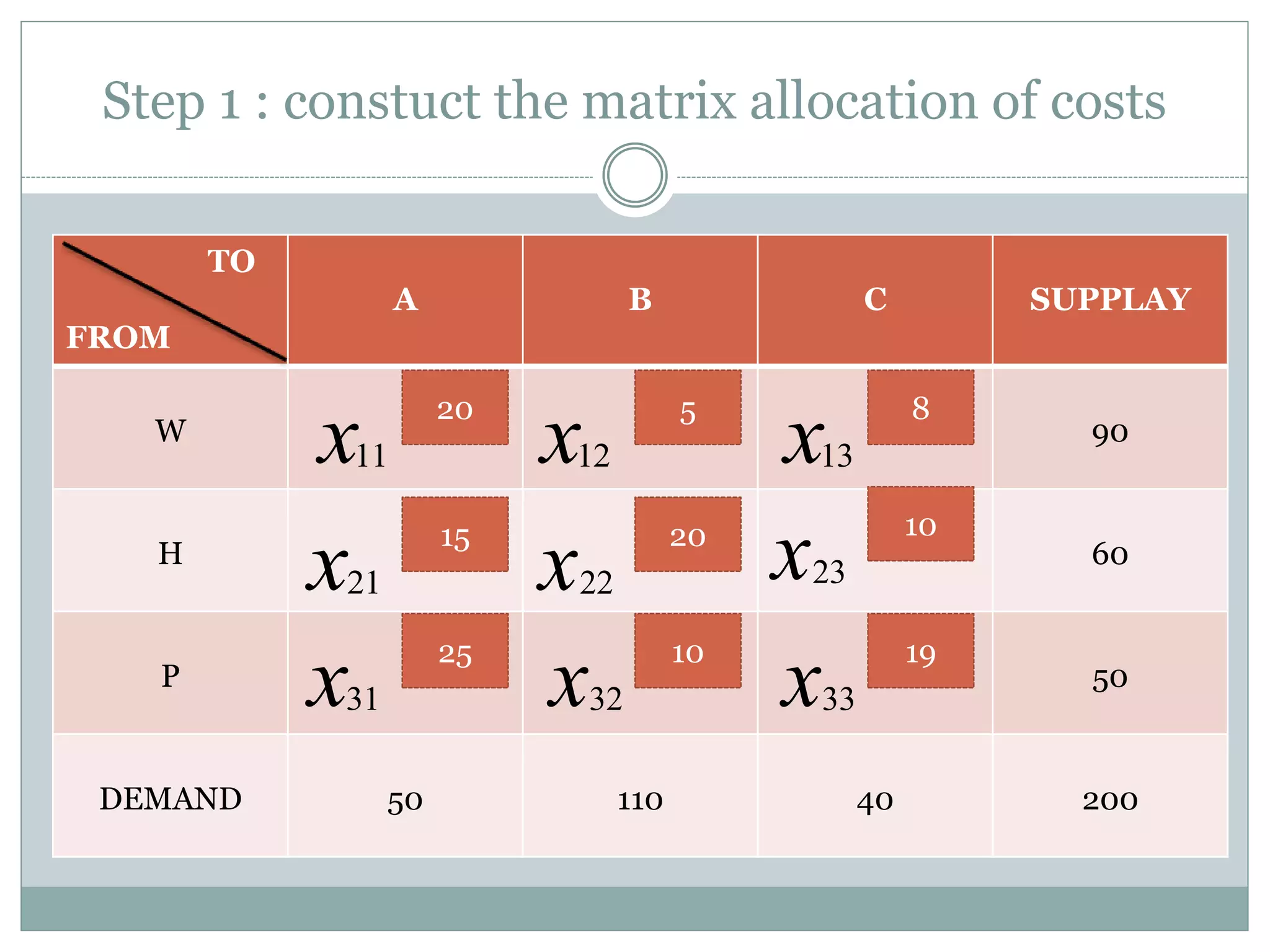
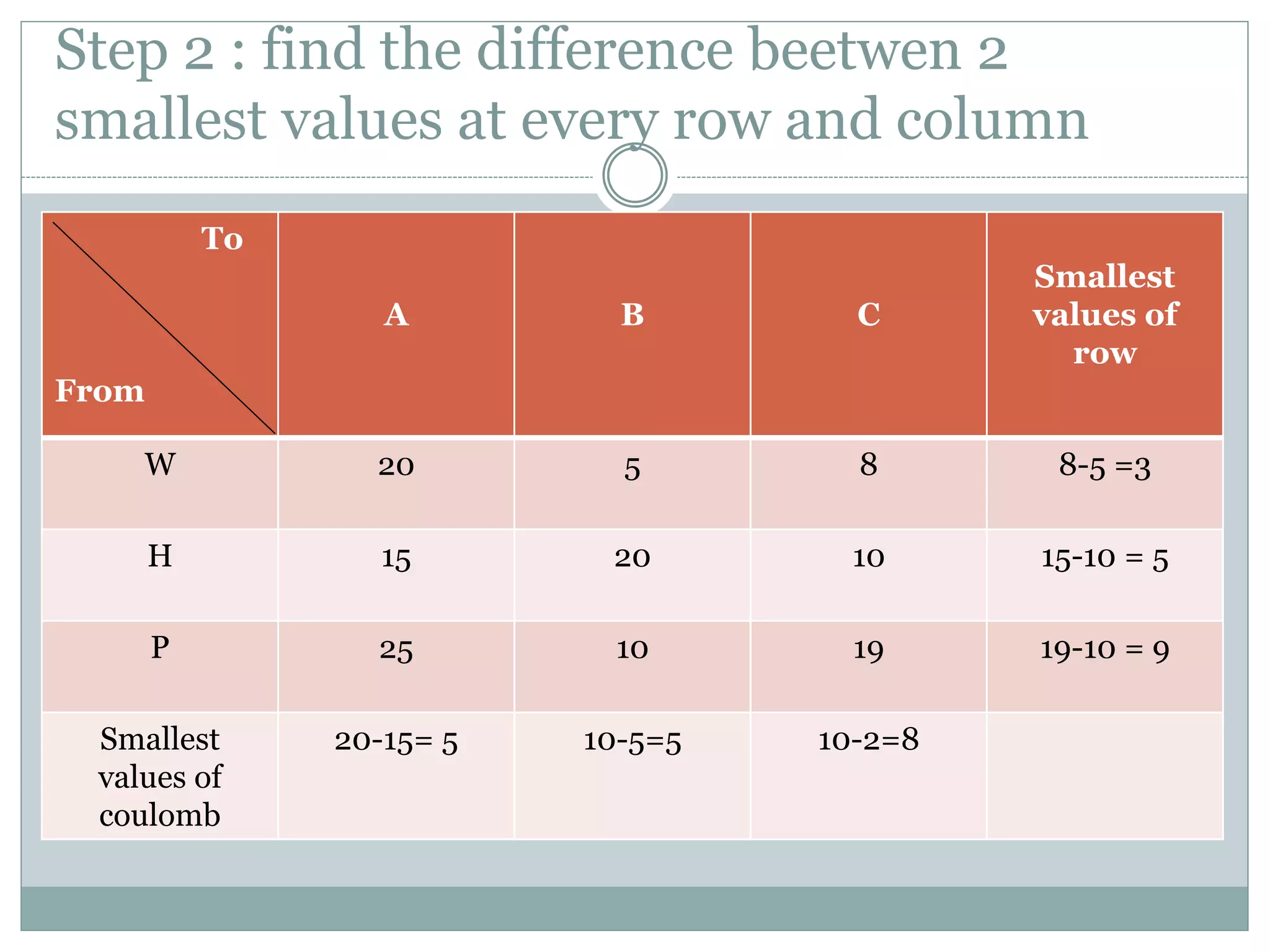
VAM (Vogel's Approximation Method) is a method for allocating resources from multiple sources to multiple destinations in a way that minimizes costs. It involves constructing a matrix of supply, demand, and transportation costs, then iteratively allocating quantities based on the lowest cost options until all supply and demand are balanced. The method is demonstrated on an example of transporting fertilizer from 3 factories to 3 markets, with the transportation costs minimized to a total of 1890 units.

1. V A M ( V O G E L ’ S A P R O X I M A T I O N M E T H O D )
English Mathematic

2. VAM (Vogel’s Approximation Method)
 The more easy and faster method for use in allocate
resources from multiple sources to multiple
destinations (market area)

3. For Example...
 a company X interested in transporting fertilizer
from three factories to three markets. Supplay
capacity, market demand in the third markets and
transport costs of unit are as follows
To
From
A B C SUPPLAY
W 20 5 8 90
H 15 20 10 60
P 25 10 19 50
DEMAND 50 110 40 200

4. Step 1 : constuct the matrix allocation of costs
TO
FROM
A B C SUPPLAY
W 90
H 60
P 50
DEMAND 50 110 40 200
20 5
15 20
25 10
8
10
19
x11
x21
x31 x32
x22
x12 x13
x23
x33

5. Step 2 : find the difference beetwen 2
smallest values at every row and column
To
From
A B C
Smallest
values of
row
W 20 5 8 8-5 =3
H 15 20 10 15-10 = 5
P 25 10 19 19-10 = 9
Smallest
values of
coulomb
20-15= 5 10-5=5 10-2=8

6. Step 3: choose the biggest difference
To
From
A B C
Smallest
values of
row
W 20 5 8 8-5 =3
H 15 20 10 15-10 = 5
P 25 10 19 19-10 = 9
Smallest
values of
coulomb
20-15= 5 10-5=5 10-2=8
Execution of value that was choosen (P row)

7. Step 4 : choose the square with lowest cost then
put it as much as you can
TO
FROM
A B C SUPPLAY
P
25 10 19
50
DEMAND 50 110 40 200
After that remove the row from table
5032
x
60

8. Step 5 : find the different again + execution again
To
From
A B C
Smallest
values of
row
W 20 5 8 8-5 =3
H 15 20 10 15-10 = 5
Smallest
values of
coulomb
20-15= 5 20-5=15 10-2=8
Remove this coulomb

9. Step 6 : find again....
To
From
A B C
Smallest
value of
row
Supplay
W 20 5 8 12 90
H 15 20 10 5 60
Smallest
value of
coulomb
5 8
Demand 50 60 40

10. Execution .........
To
From
A B C SUPPLAY
W
60 30
90
H 60
P
50
50
DEMAND
50 110 40
200
20 5
15 20
25 10
8
10
19

11. Finaalllllll.............
TO
FROM
A B C SUPPLAY
W 60 30
90
H 50 10
60
P 50
50
DEMAND 50 110 40
200
20 5
15 20
25 10
8
10
19
So the transportation cost = 60*5+30*8 + 50*15 + 10*10 + 50*10 = 1890