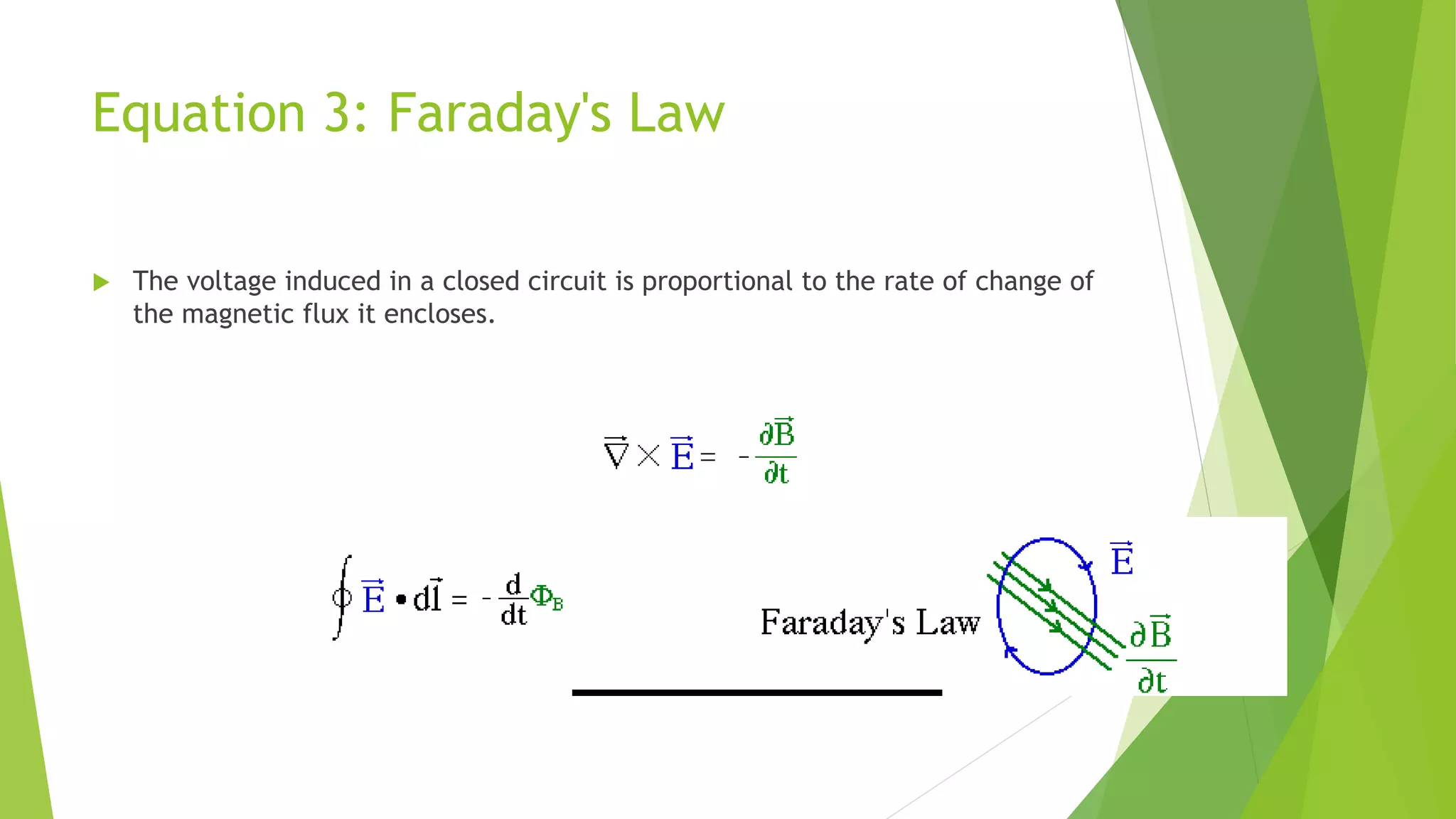
The document discusses the concepts of electrical conductivity, describing how materials conduct electricity and differentiating between conductors, insulators, and semiconductors. It explains Maxwell's equations, formulated by James Clerk Maxwell, which unify key electromagnetic principles and demonstrate the propagation and interaction of electric and magnetic fields. The summary of each of Maxwell's four equations is also provided, highlighting their significance in electromagnetics and antenna theory.

1. Electric Field in Material
Space
Irfan Sultan
Instructor

2. Conductivity and Types of Materials
 Electrical conductivity is a measure of a material's ability to conduct an electric
current. Its unit is mho/m or Siemens/m.
 Electrical conductance is an electrical phenomenon where a material contains
movable particles with electric charge (such as electrons), which can carry
electricity. When a difference of electrical potential is placed across a conductor,
its electrons flow, and an electric current appears.
 It normally varies with:
 Temperature
 Frequency
 Conductors: Conductivity >> 1
 Insulators: Conductivity <<1
 Semiconductors: Have conductivity values b/w those of conductors and insulators.

3. Maxwell’s Equations
 James Clerk Maxwell [1831-1879] was an Einstein/Newton-level genius who
took a set of known experimental laws (Faraday's Law, Ampere's Law) and
unified them into a symmetric coherent set of Equations known as Maxwell's
Equations. Maxwell was one of the first to determine the speed of
propagation of electromagnetic (EM) waves was the same as the speed of light
- and hence to conclude that EM waves and visible light were really the same
thing.
 Maxwell's Equations are a set of 4 complicated equations that describe the
world of electromagnetics. These equations describe how electric and
magnetic fields propagate, interact, and how they are influenced by objects.
 Maxwell's Equations are critical in understanding Antennas and
Electromagnetics.

4. Maxwell’s Equations
 Equation 1: Gauss’s Law
 Equation 2: Gauss’s Magnetism Law
 Equation 3: Faraday's Law
 Equation 4: Ampere's Law

5. Equation 1: Gauss’s Law
 The electric flux leaving a volume is proportional to the charge inside.

6. Equation 2: Gauss’s Law For Magnetism
 There are no magnetic monopoles; the total magnetic flux through a closed
surface is zero.

7. Equation 3: Faraday's Law
 The voltage induced in a closed circuit is proportional to the rate of change of
the magnetic flux it encloses.

8. Equation 4: Ampere's Law
 The magnetic field induced around a closed loop is proportional to the
electric current plus displacement current (rate of change of electric field) it
encloses.

9. Maxwell’s Equations: Summary