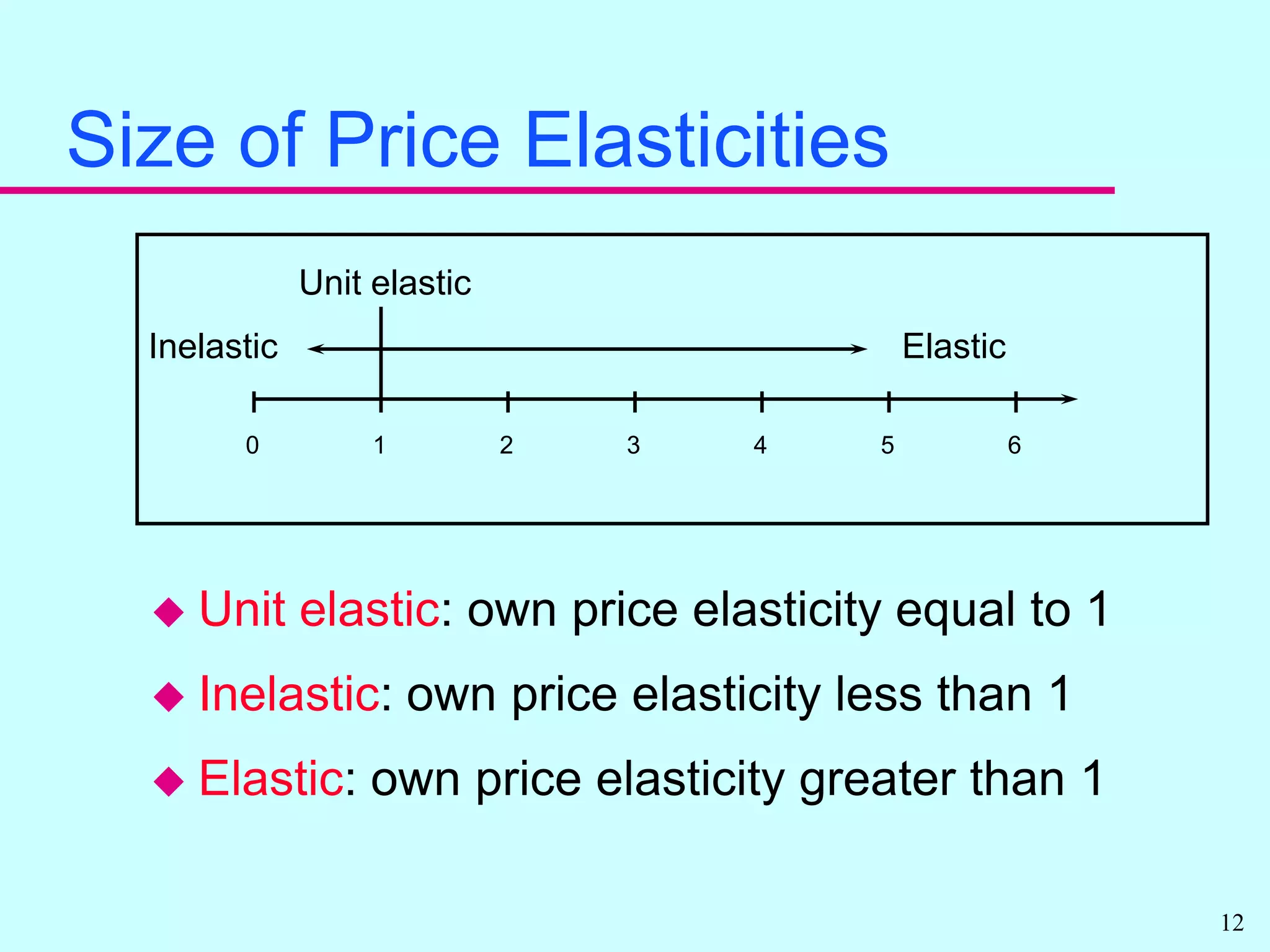
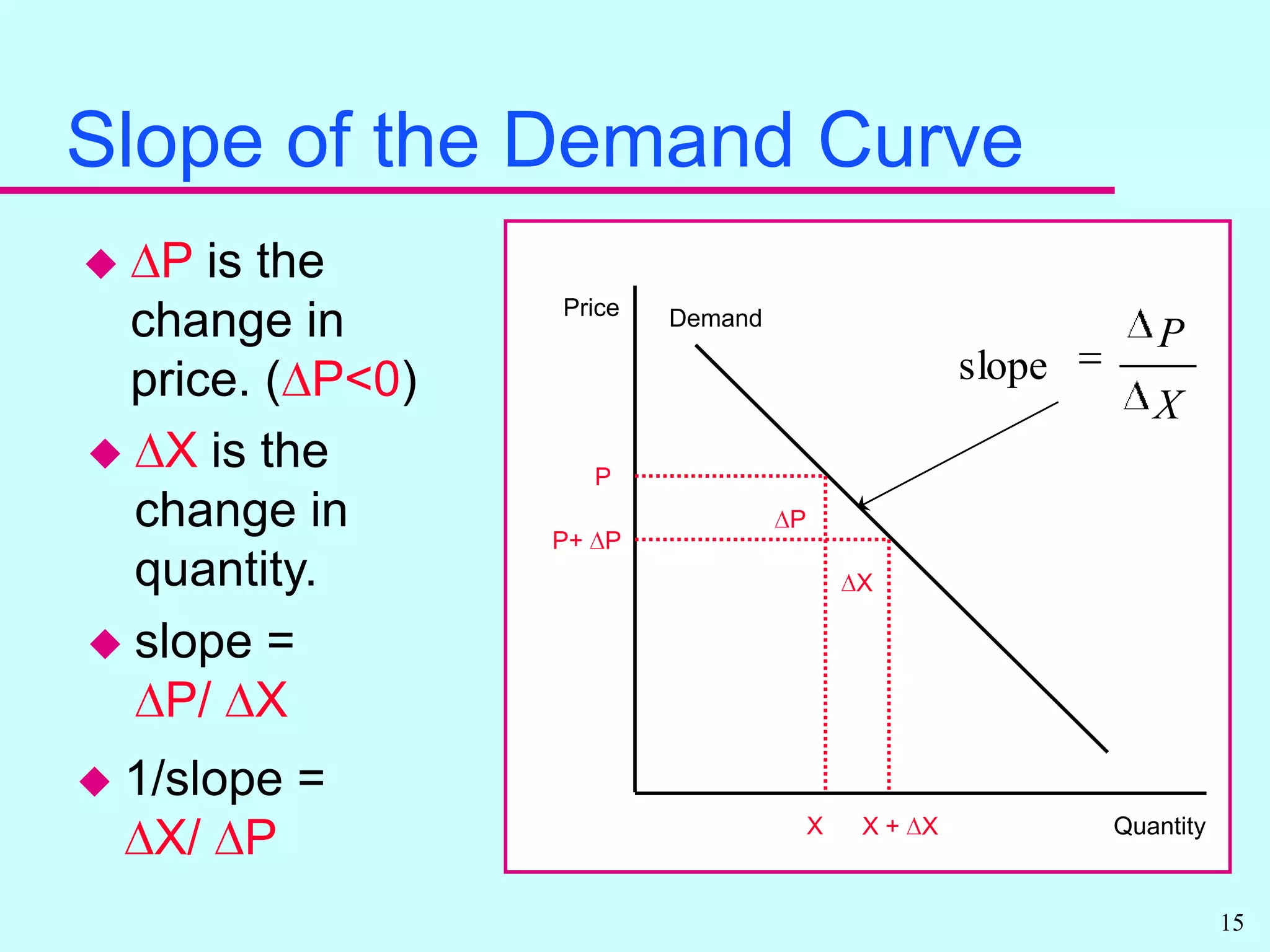
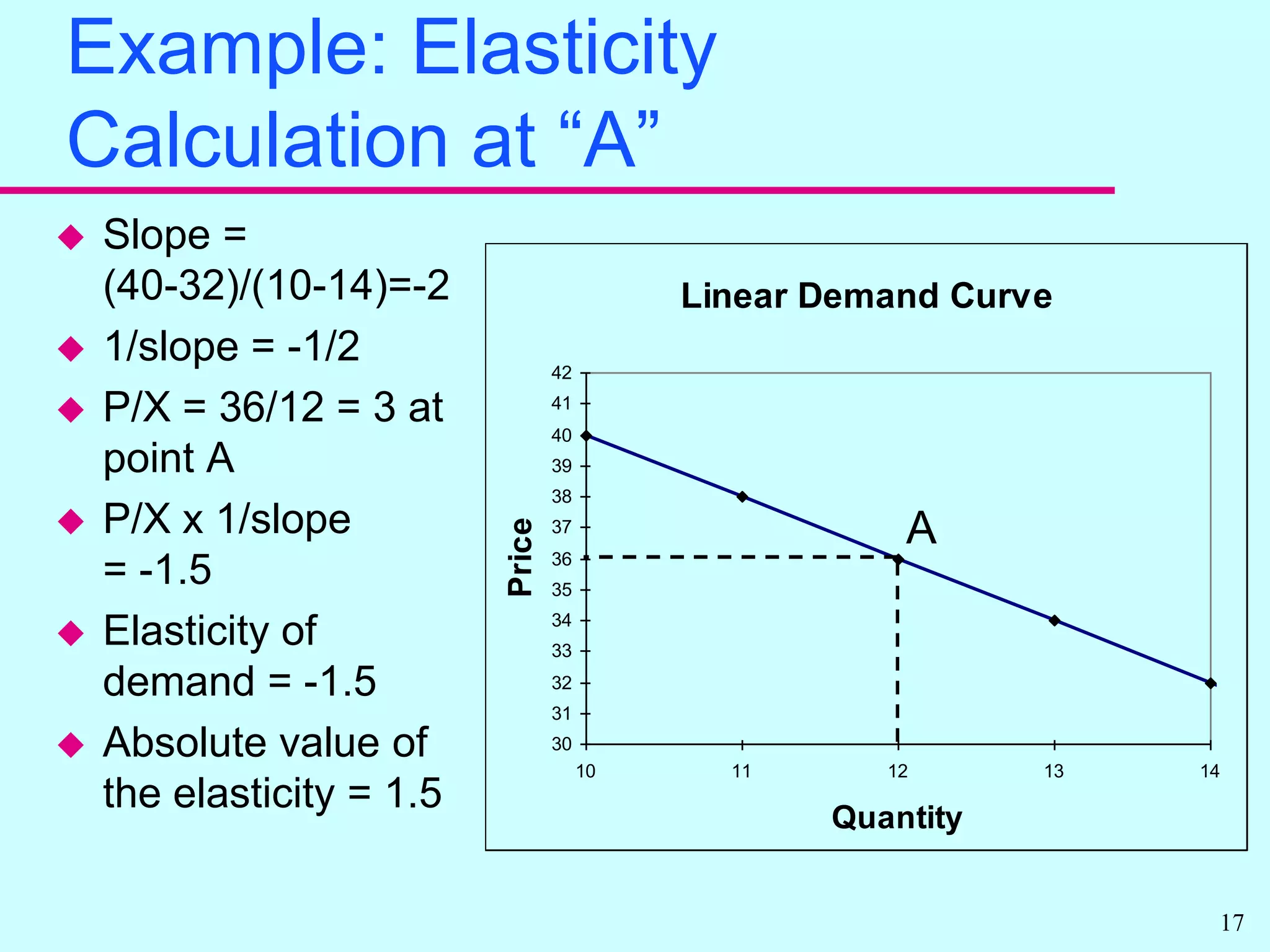
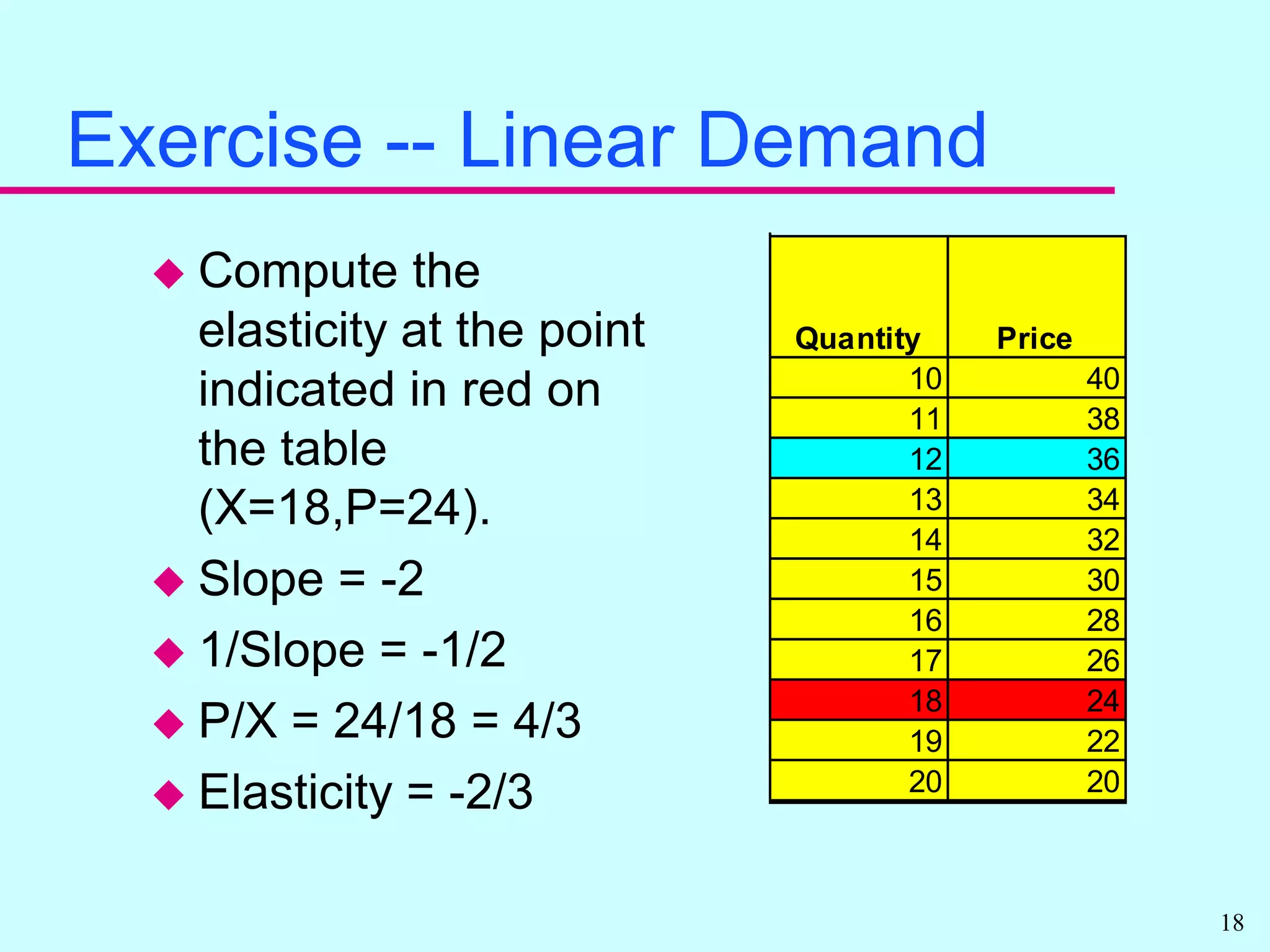
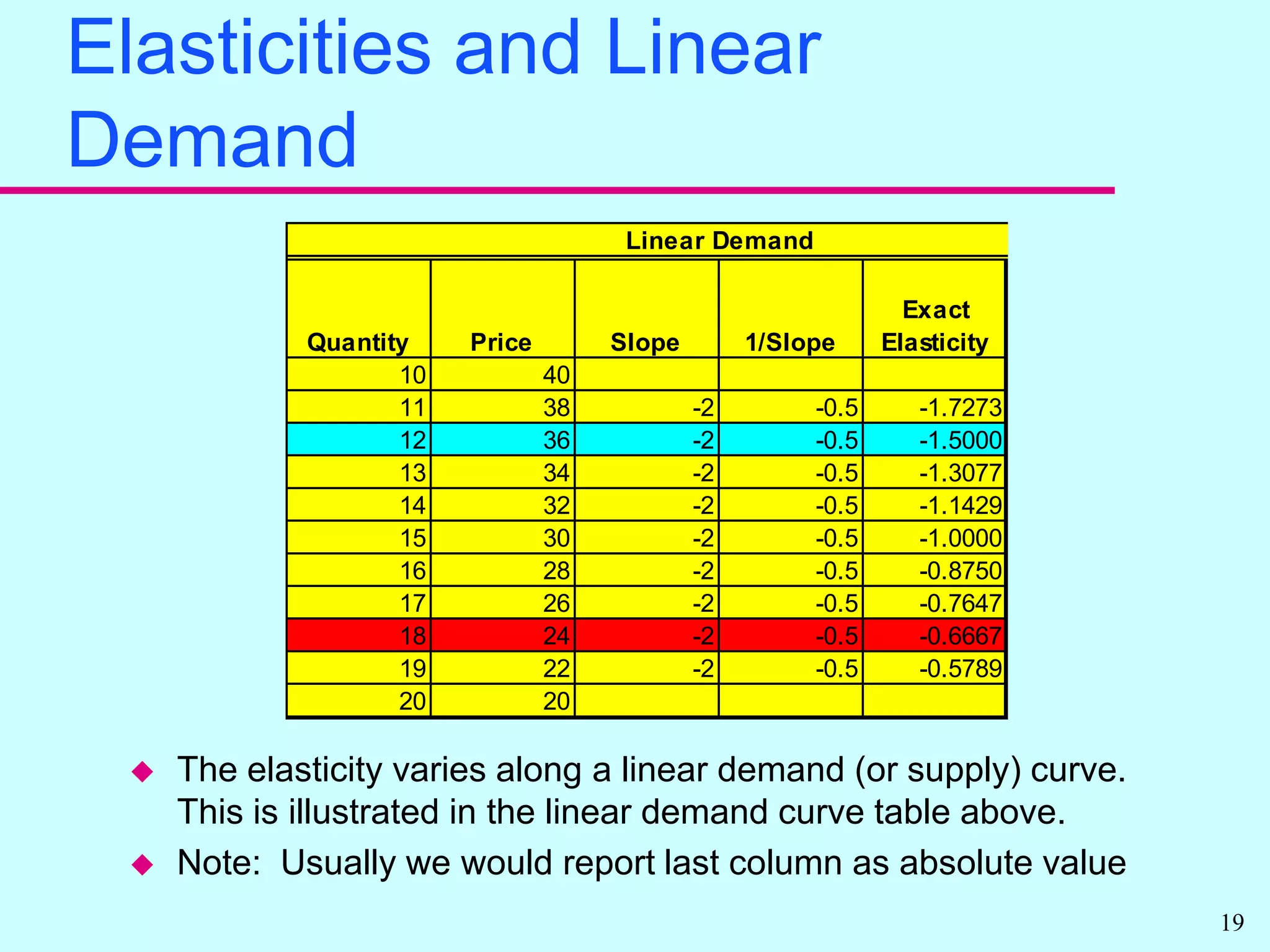
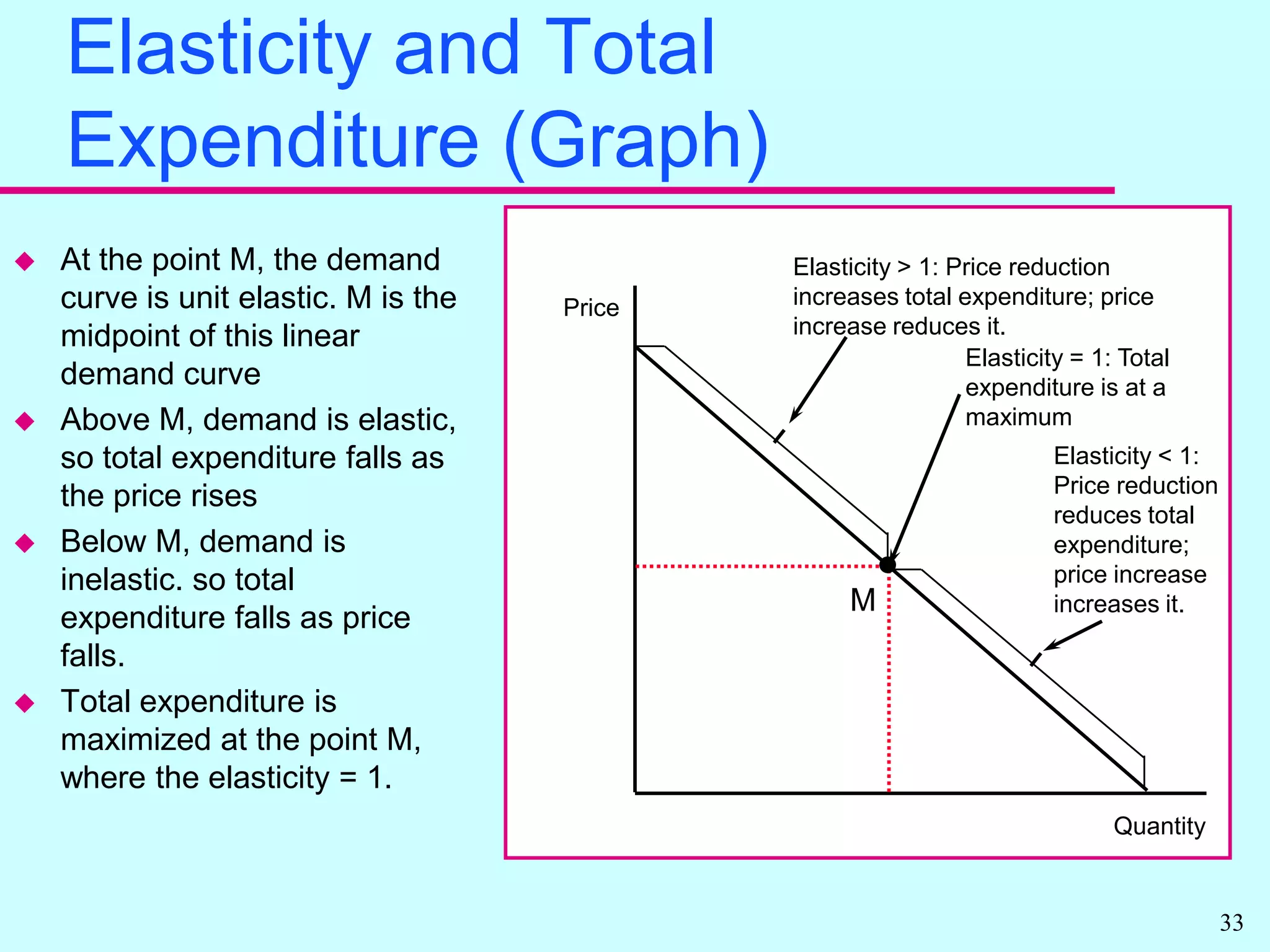
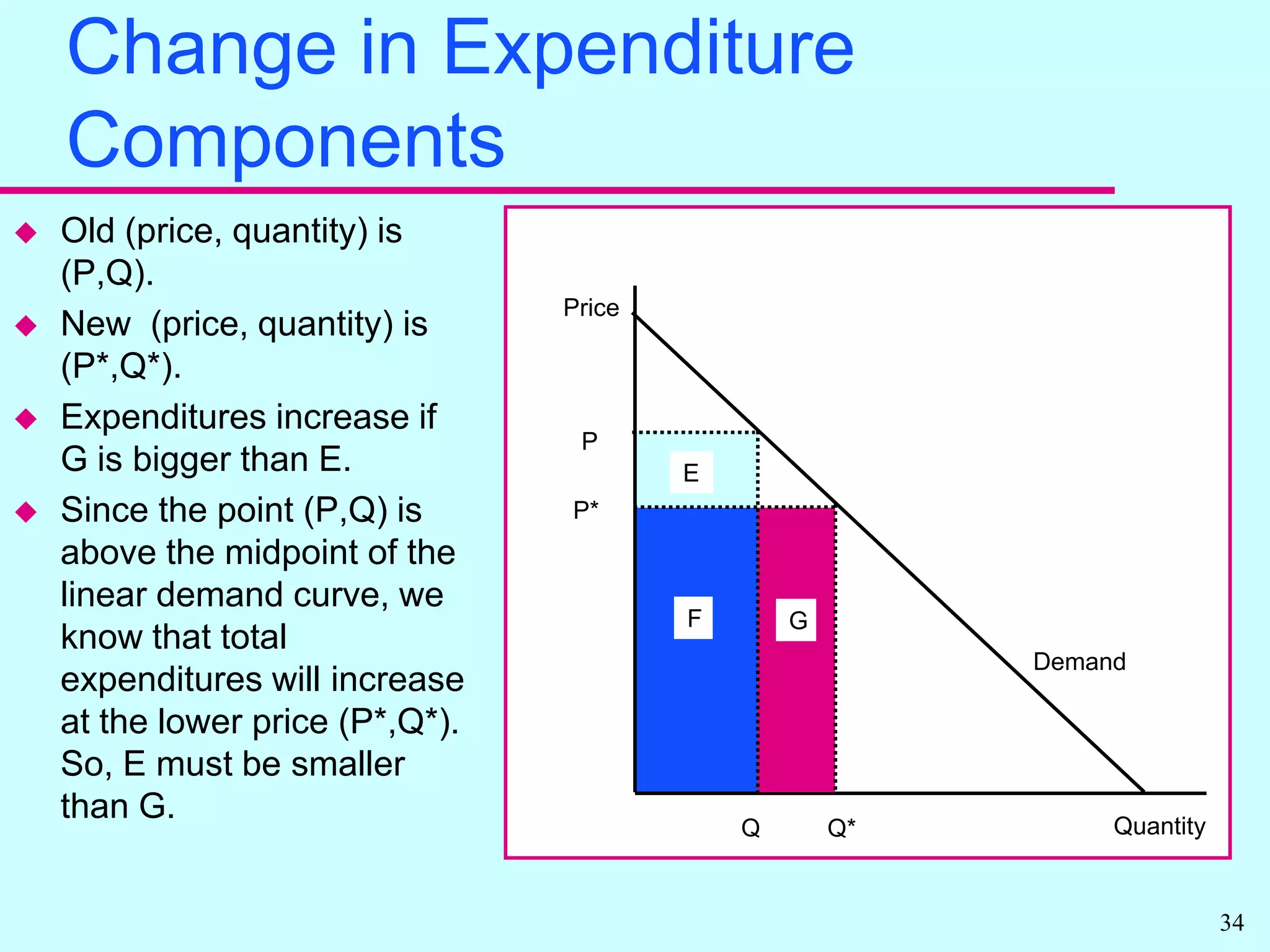
Elasticity measures the responsiveness of quantity to price changes. It allows economists to compare markets without standardizing units. There are own price elasticities of demand and supply that measure responsiveness of quantity to the good's own price. Demand is more price sensitive when elasticity is further from zero. Total expenditures can increase or decrease with price changes depending on elasticity. Other elasticities include cross price and income elasticities.

1. Elasticity

2. Elasticity measuresWhat are they?Responsiveness measuresWhy introduce them?Demand and supply responsiveness clearly matters for lots of market analyses.Why not just look at slope?Want to compare across markets: inter market Want to compare within markets: intra marketslope can be misleadingwant a unit free measure

3. Why Economists Use ElasticityAn elasticity is a unit-free measure.By comparing markets using elasticities it does not matter how we measure the price or the quantity in the two markets.Elasticities allow economists to quantify the differences among markets without standardizing the units of measurement.

4. What is an Elasticity?Measurement of the percentage change in one variable that results from a 1% change in another variable.Can come up with many elasticities.We will introduce four.three from the demand functionone from the supply function

5. 2 VIP ElasticitiesPrice elasticity of demand: how sensitive is the quantity demanded to a change in the price of the good.Price elasticity of supply: how sensitive is the quantity supplied to a change in the price of the good.Often referred to as “own” price elasticities.

6. Examples of Own Price Demand ElasticitiesWhen the price of gasoline rises by 1% the quantity demanded falls by 0.2%, so gasoline demand is not very price sensitive.Price elasticity of demand is -0.2 .When the price of gold jewelry rises by 1% the quantity demanded falls by 2.6%, so jewelry demand is very price sensitive.Price elasticity of demand is -2.6 .

7. Examples of Own PriceSupply ElasticitiesWhen the price of DaVinci paintings increases by 1% the quantity supplied doesn’t change at all, so the quantity supplied of DaVinci paintings is completely insensitive to the price.Price elasticity of supply is 0.When the price of beef increases by 1% the quantity supplied increases by 5%, so beef supply is very price sensitive.Price elasticity of supply is 5.

8. Examples of Unit-free ComparisonsGasoline and jewelry It doesn’t matter that gas is sold by the gallon for about $1.09 and gold is sold by the ounce for about $290.We compare the demand elasticities of -0.2 (gas) and -2.6 (gold jewelry).Gold jewelry demand is more price sensitive.

9. Examples of Unit-free ComparisonsPaintings and meat It doesn’t matter that classical paintings are sold by the canvas for millions of dollars each while beef is sold by the pound for about $1.50.We compare the supply elasticities of 0 (classical paintings) and 5 (beef).Beef supply is more price sensitive.

10. Inelastic Economic RelationsWhen an elasticity is small (between 0 and 1 in absolute value), we call the relation that it describes inelastic.Inelastic demand means that the quantity demanded is not very sensitive to the price.Inelastic supply means that the quantity supplied is not very sensitive to the price.

11. Elastic Economic RelationsWhen an elasticity is large (greater than 1 in absolute value), we call the relation that it describes elastic.Elastic demand means that the quantity demanded is sensitive to the price.Elastic supply means that the quantity supplied is sensitive to the price.

12. Size of Price Elasticities0123456Unit elasticInelasticElasticUnit elastic: own price elasticity equal to 1Inelastic: own price elasticity less than 1

13. Elastic: own price elasticity greater than 1General Formula for own price elasticity of demandP = Current price of good XXD = Quantity demanded at that priceDP = Small change in the current priceDXD= Resulting change in quantity demanded

14. Point Formula for Own Price Elasticity of DemandThe exact formula for calculating an elasticity at the point A on the demand curve.Note: we’ll take absolute value

15. Slope of the Demand CurvePriceDemandPDPP+ DPDXQuantityXX + DXDP is the change in price. (DP<0)DX is the change in quantity.

16. slope = DP/ DX

17. 1/slope = DX/ DPSlope Compared to ElasticityThe slope measures the rate of change of one variable (P, say) in terms of another (X, say).The elasticity measures the percentage change of one variable (X, say) in terms of another (P, say).

18. Example: Elasticity Calculation at “A”Slope = (40-32)/(10-14)=-21/slope = -1/2P/X = 36/12 = 3 at point AP/X x 1/slope= -1.5Elasticity of demand = -1.5 Absolute value of the elasticity = 1.5

19. Exercise -- Linear DemandCompute the elasticity at the point indicated in red on the table (X=18,P=24).Slope = -21/Slope = -1/2P/X = 24/18 = 4/3Elasticity = -2/3

20. Elasticities and Linear DemandThe elasticity varies along a linear demand (or supply) curve. This is illustrated in the linear demand curve table above. Note: Usually we would report last column as absolute value

21. Supply ElasticitiesThe price elasticity of supply is always positive.Economists refer to the price elasticity of supply by its actual value.Exactly the same type of point and arc formulas are used to compute and estimate supply elasticities as for demand elasticities.

22. Some Technical Definitions For Extreme Elasticity ValuesEconomists use the terms “perfectly elastic” and “perfectly inelastic” to describe extreme values of price elasticities. Perfectly elastic means the quantity (demanded or supplied) is as price sensitive as possible.Perfectly inelastic means that the quantity (demanded or supplied) has no price sensitivity at all.

23. Perfectly Elastic DemandPricePerfectly Elastic Demand (elasticity = ¥)QuantityWe say that demand is perfectly elastic when a 1% change in the price would result in an infinite change in quantity demanded.

24. Perfectly Inelastic DemandPricePerfectly Inelastic Demand (elasticity = 0)QuantityWe say that demand is perfectly inelastic when a 1% change in the price would result in no change in quantity demanded.

25. Perfectly Elastic SupplyPricePerfectly Elastic Supply (elasticity = ¥)QuantityWe say that supply is perfectly elastic when a 1% change in the price would result in an infinite change in quantity supplied.

26. Perfectly Inelastic SupplyPricePerfectly Inelastic Supply (elasticity = 0)QuantityWe say that supply is perfectly inelastic when a 1% change in the price would result in no change in quantity supplied.

27. Determinants of elasticityWhat is a major determinant of the own price elasticity of demand? Availability of substitutes in consumption.What is a major determinant of the own price elasticity of supply? Availability of alternatives in production.

28. Using Demand Elasticity: Total ExpendituresDo the total expenditures on a product go up or down when the price increases?The price increase means more spent for each unit.But, quantity demanded declines as price rises.So, we must measure the measure the price elasticity of demand to answer the question.

29. Bridge Toll ExampleCurrent toll for the George Washington Bridge is $2.00/trip. Suppose the quantity demanded at $2.00/trip is 100,000 trips/hour. If the price elasticity of demand for bridge trips is 2.0, what is the effect of a 10% toll increase?

30. Bridge Toll: Elastic DemandPrice elasticity of demand = 2.0Toll increase of 10% implies a 20% decline in the quantity demanded.Trips fall to 80,000/hour.Total expenditure falls to $176,000/hour (= 80,000 x $2.20).$176,000 < $200,000, the revenue from a $2.00 toll.

31. Bridge Toll Example, Part 2Now suppose the elasticity of demand for bridge trips is 0.5.How would the number of trips and the expenditure on tolls be affected by a 10% increase in the toll?

32. Bridge Toll: Inelastic DemandPrice elasticity of demand = 0.5Toll increase of 10% implies a 5% decline in the quantity demanded.Trips fall to 95,000/hour.Total expenditure rises to $209,000/hour (= 95,000 x $2.20).$209,000 > $200,000, the revenue from a $2.00 toll.

33. Elasticity and Total ExpendituresA price increase will increase total expenditures if, and only if, the price elasticity of demand is less than 1 in absolute value (between -1 and zero)Inelastic demandA price reduction will increase total expenditures if, and only if, the price elasticity of demand is greater than 1 in absolute value (less than -1).Elastic demand

34. Elasticity and Total Expenditure (Graph)At the point M, the demand curve is unit elastic. M is the midpoint of this linear demand curveAbove M, demand is elastic, so total expenditure falls as the price risesBelow M, demand is inelastic. so total expenditure falls as price falls.Total expenditure is maximized at the point M, where the elasticity = 1.Elasticity > 1: Price reduction increases total expenditure; price increase reduces it. PriceElasticity = 1: Total expenditure is at a maximumElasticity < 1: Price reduction reduces total expenditure; price increase increases it. MQuantity

35. Change in Expenditure ComponentsOld (price, quantity) is (P,Q).New (price, quantity) is (P*,Q*).Expenditures increase if G is bigger than E.Since the point (P,Q) is above the midpoint of the linear demand curve, we know that total expenditures will increase at the lower price (P*,Q*). So, E must be smaller than G.PricePEP*FGDemandQuantityQQ*

36. Two real world examplesGas taxes in Washington DCVanity plates in Virginia

37. Other Price Elasticities: Cross- Price Elasticity of DemandElasticity of demand with respect to the price of a complementary good (cross-price elasticity)This elasticity is negative because as the price of a complementary good rises, the quantity demanded of the good itself falls.Example (from last week) software is complementary with computers. When the price of software rises the quantity demanded of computers falls.Cross-price elasticity quantifies this effect.

38. Other Price Elasticities: Cross Price Elasticity of DemandElasticity of demand with respect to the price of a substitute good (also a cross-price elasticity)This elasticity is positive because as the price of a substitute good rises, the quantity demanded of the good itself rises.Example (from last week) hockey is substitute for basketball. When the price of hockey tickets rises the quantity demanded of basketball tickets rises.Cross-price elasticity quantifies this effect.

39. Other Elasticities: Income Elasticity of DemandThe elasticity of demand with respect to a consumer’s income is called the income elasticity.When the income elasticity of demand is positive (normal good), consumers increase their purchases of the good as their incomes rise (e.g. automobiles, clothing).When the income elasticity of demand is greater than 1 (luxury good), consumers increase their purchases of the good more than proportionate to the income increase (e.g. ski vacations).When the income elasticity of demand is negative (inferior good), consumers reduce their purchases of the good as their incomes rise (e.g. potatoes).