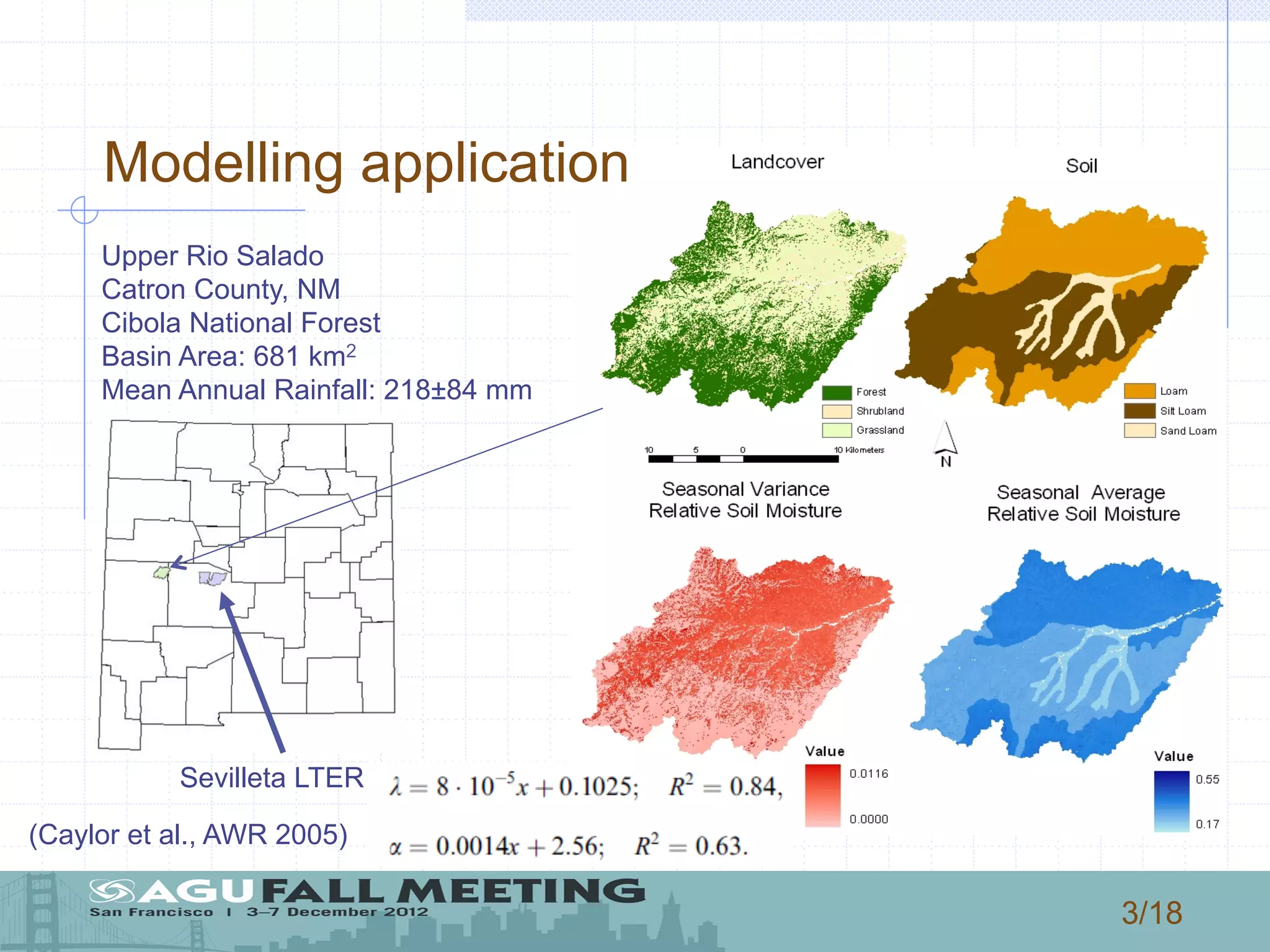
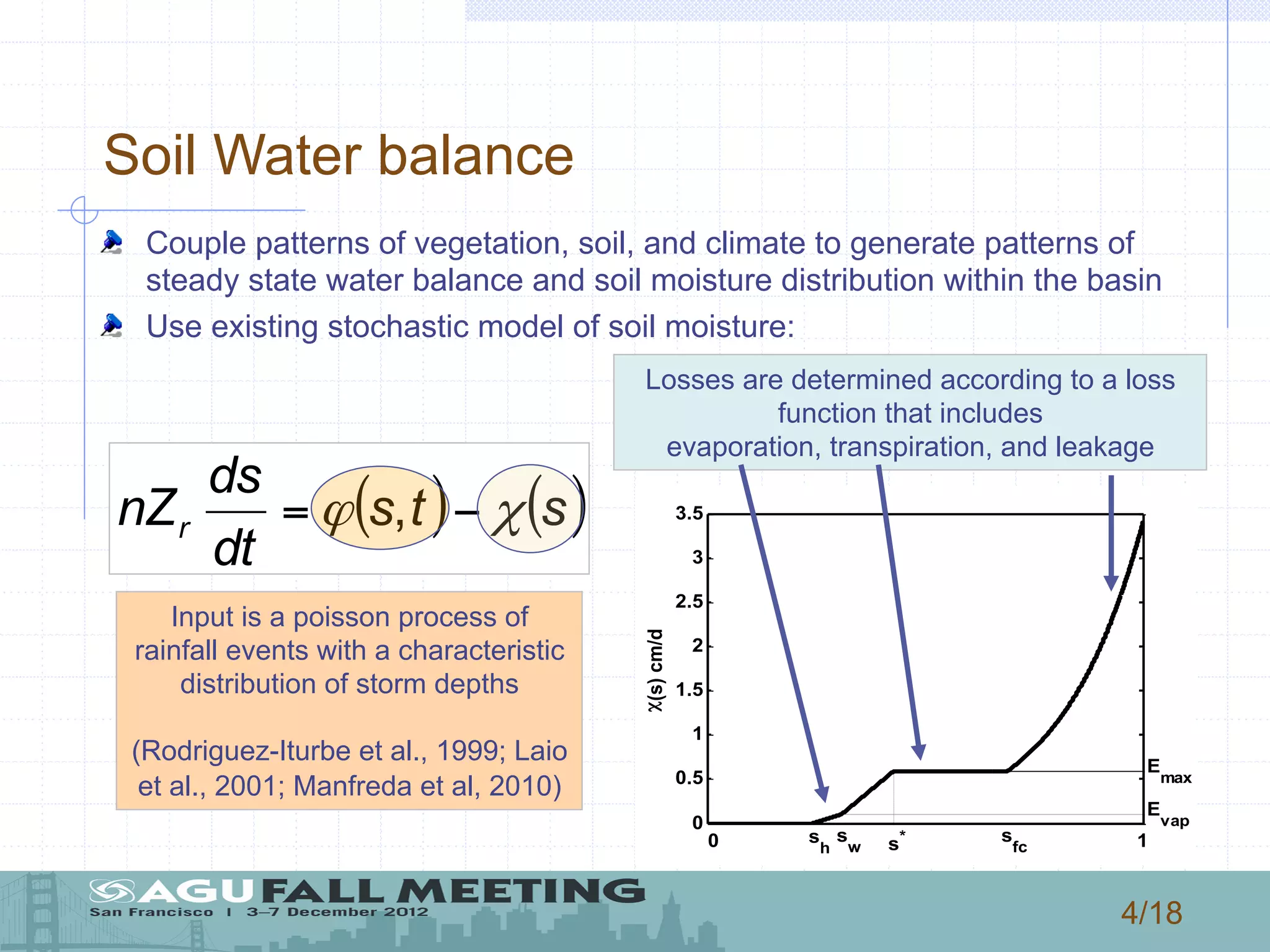
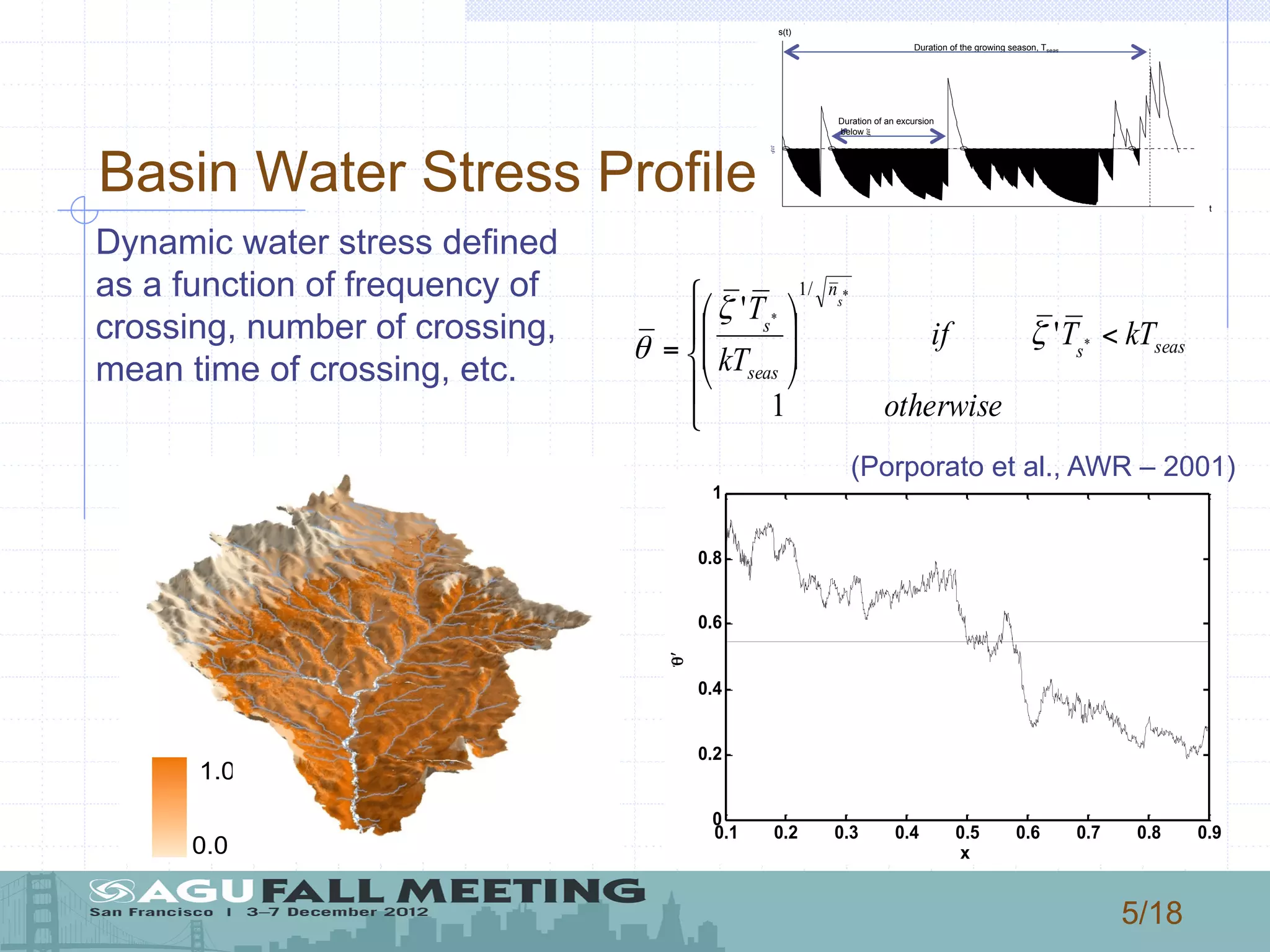
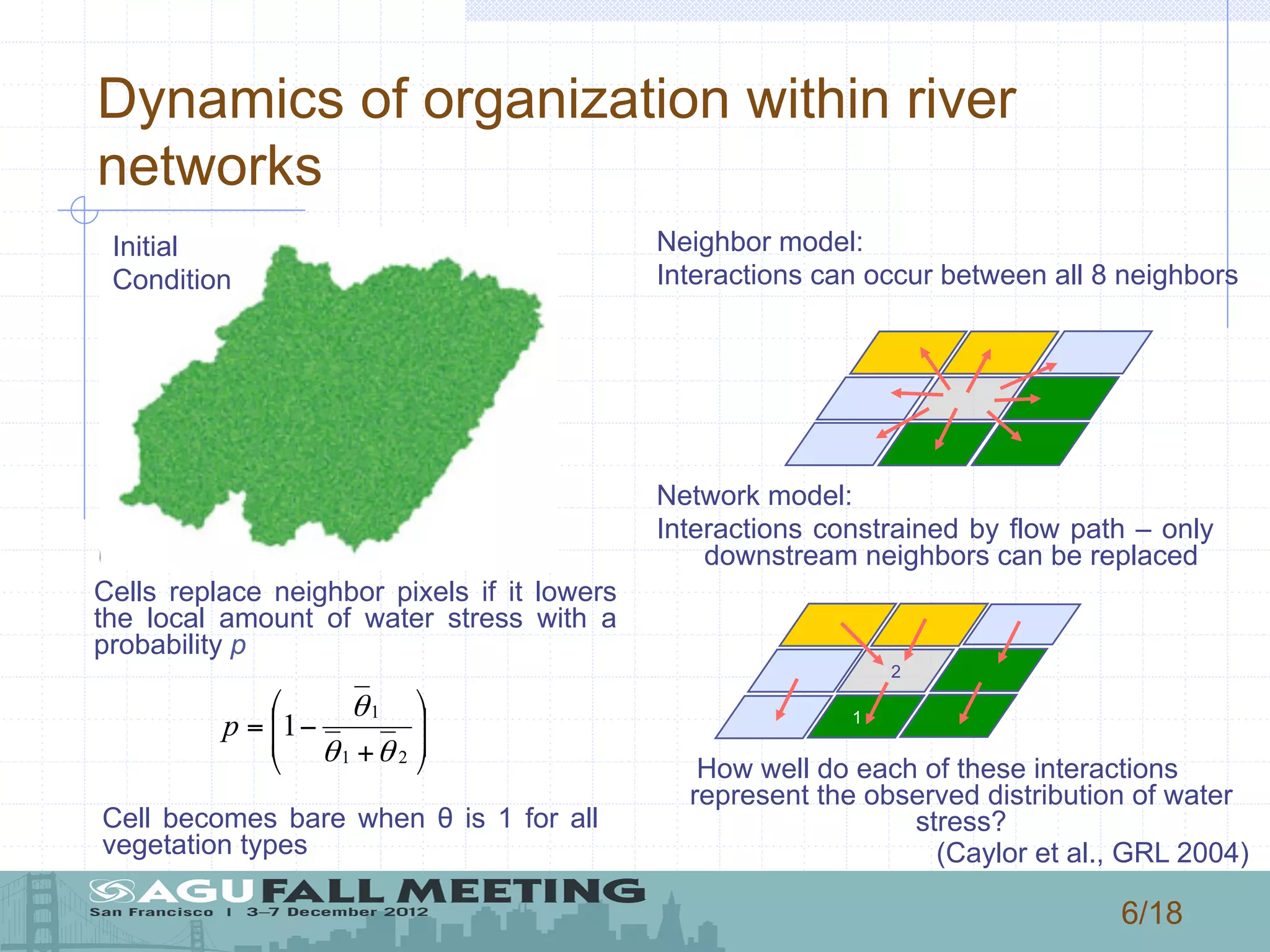
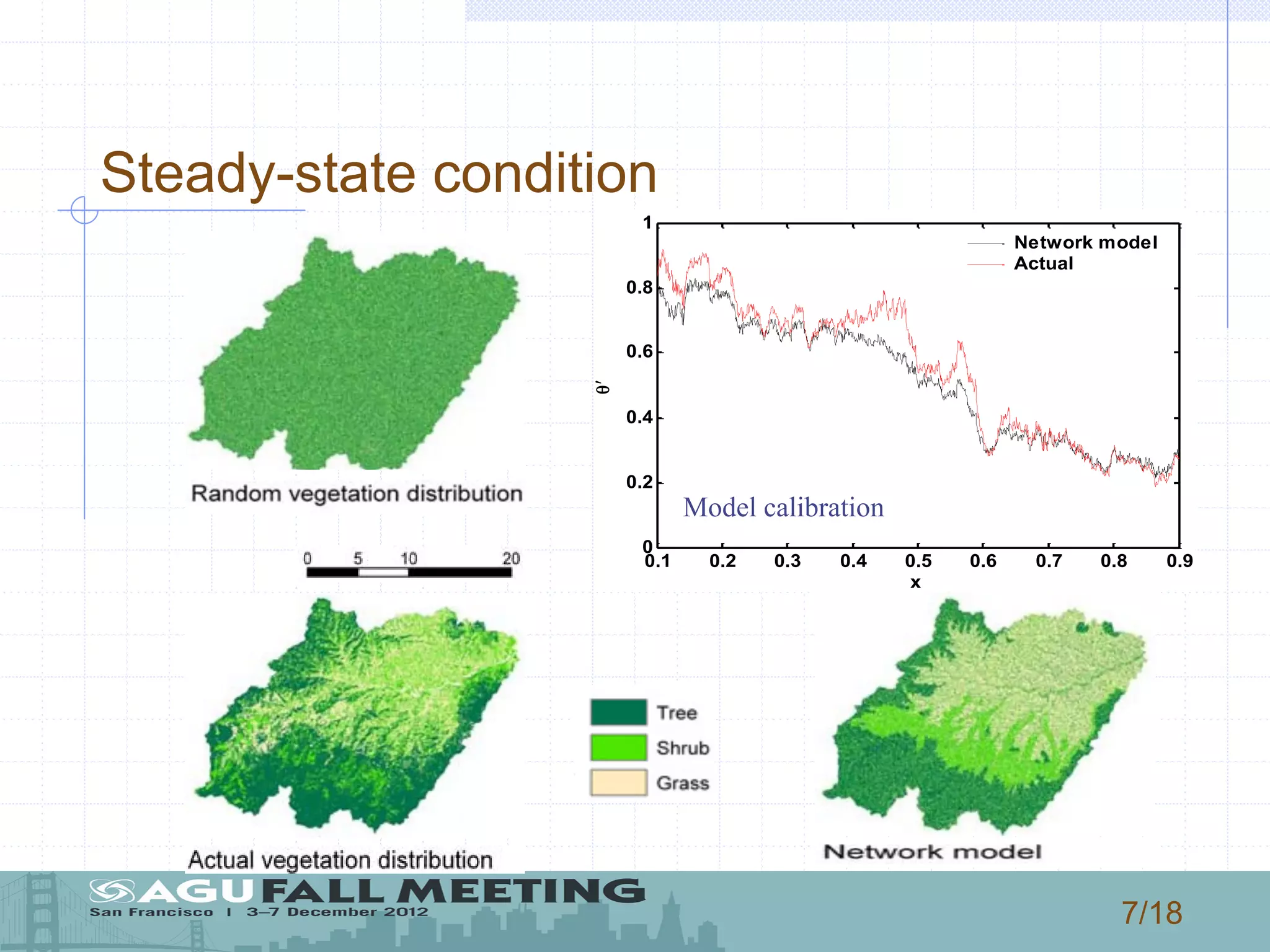
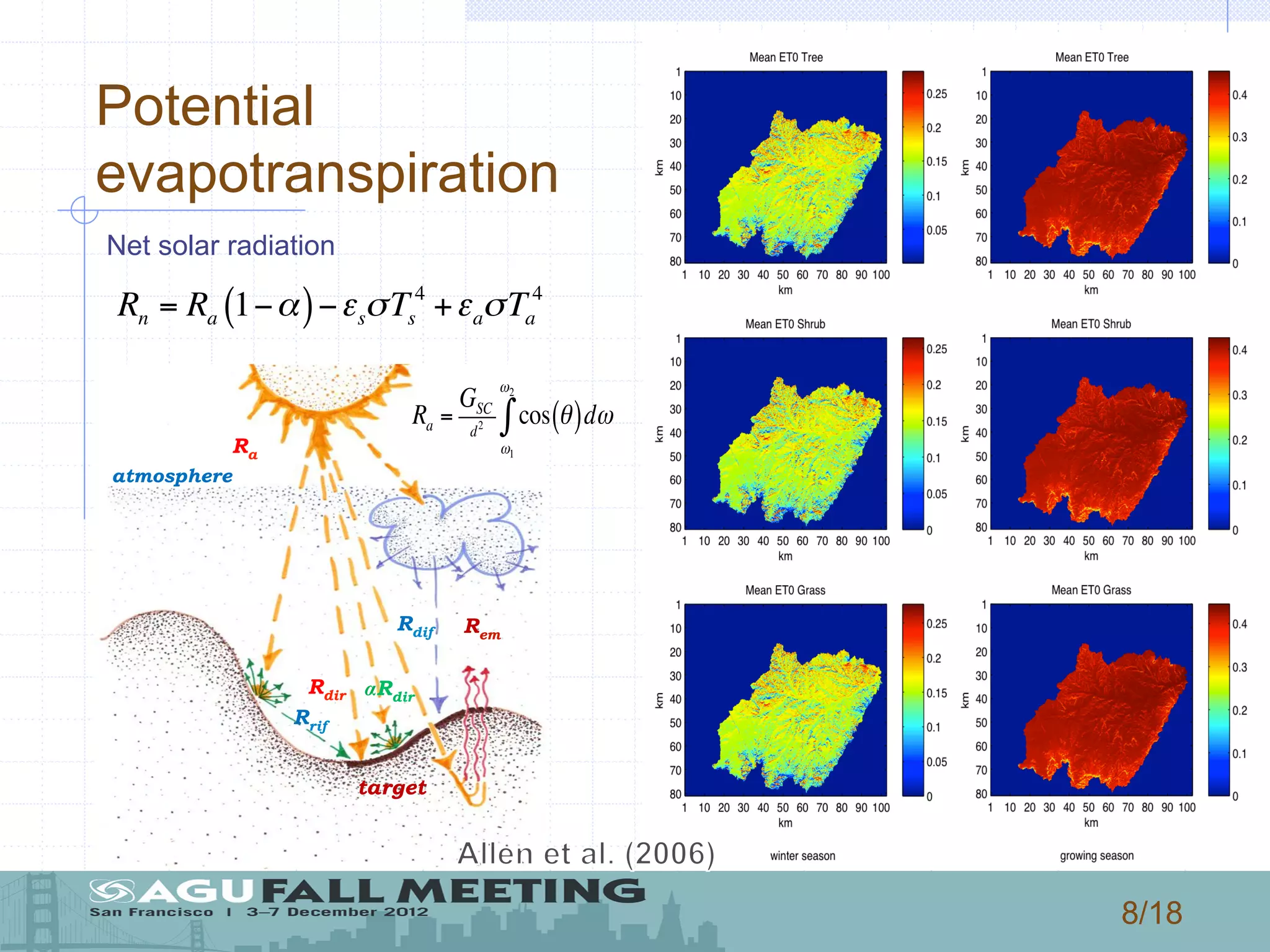
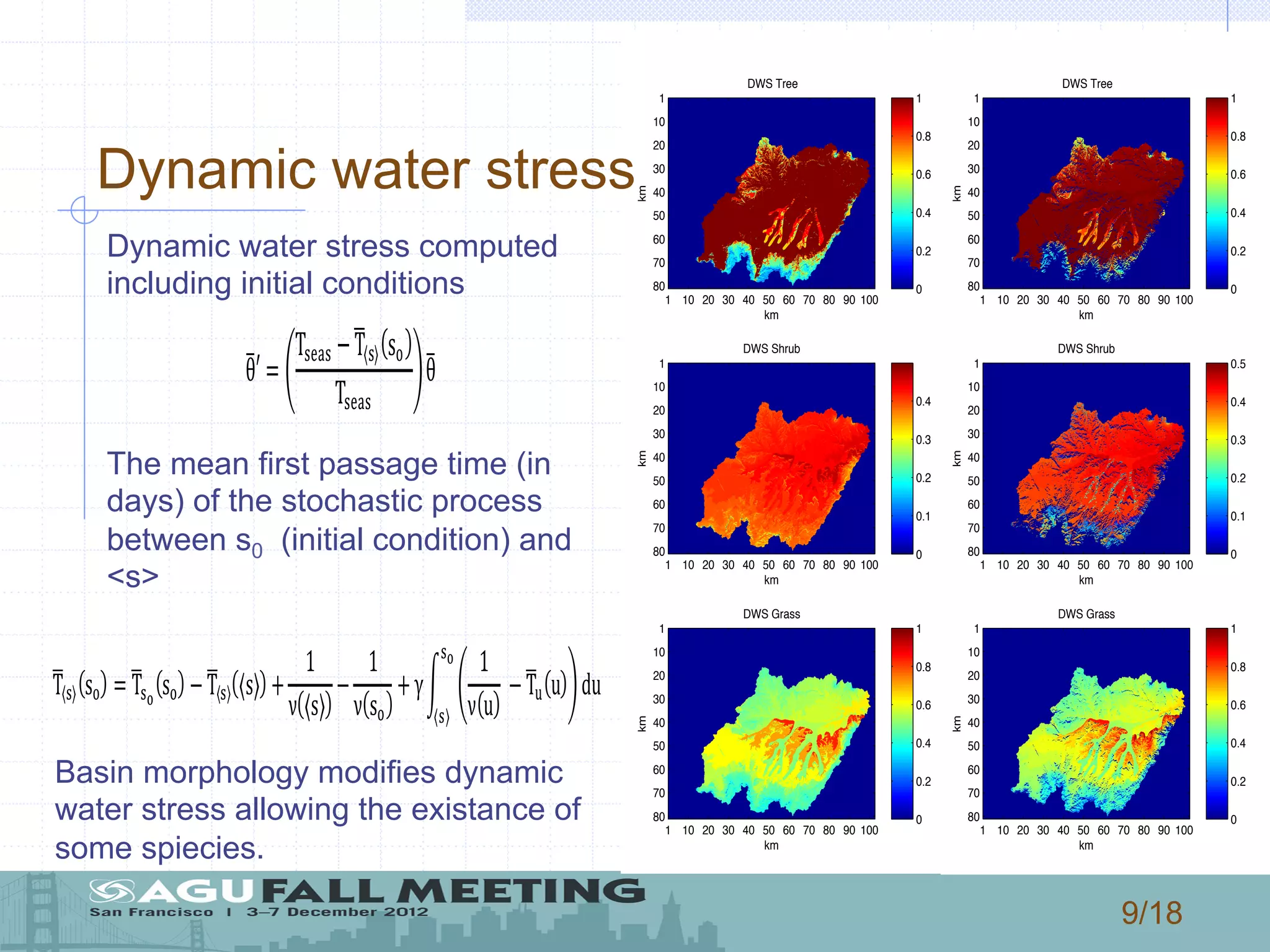
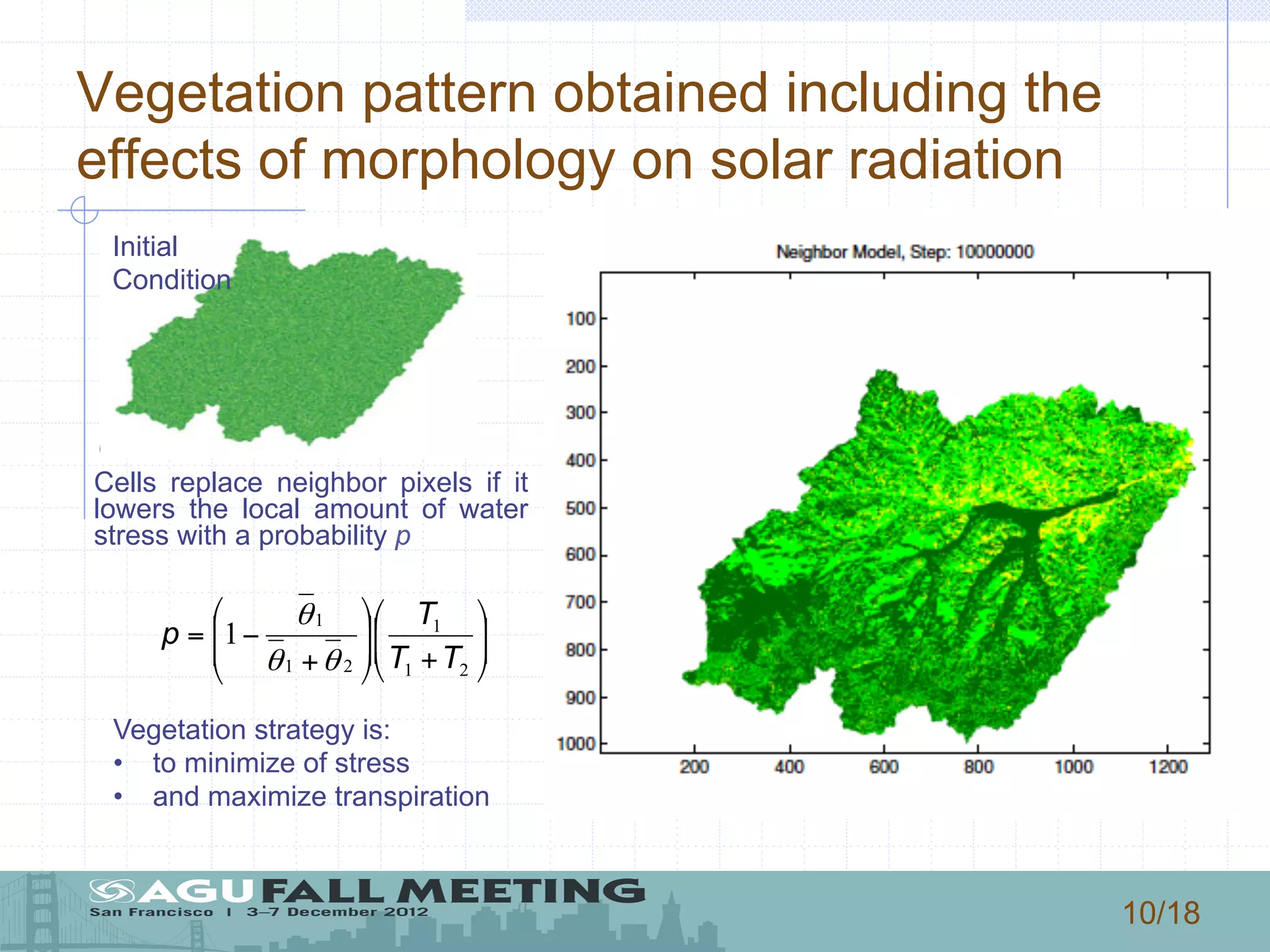
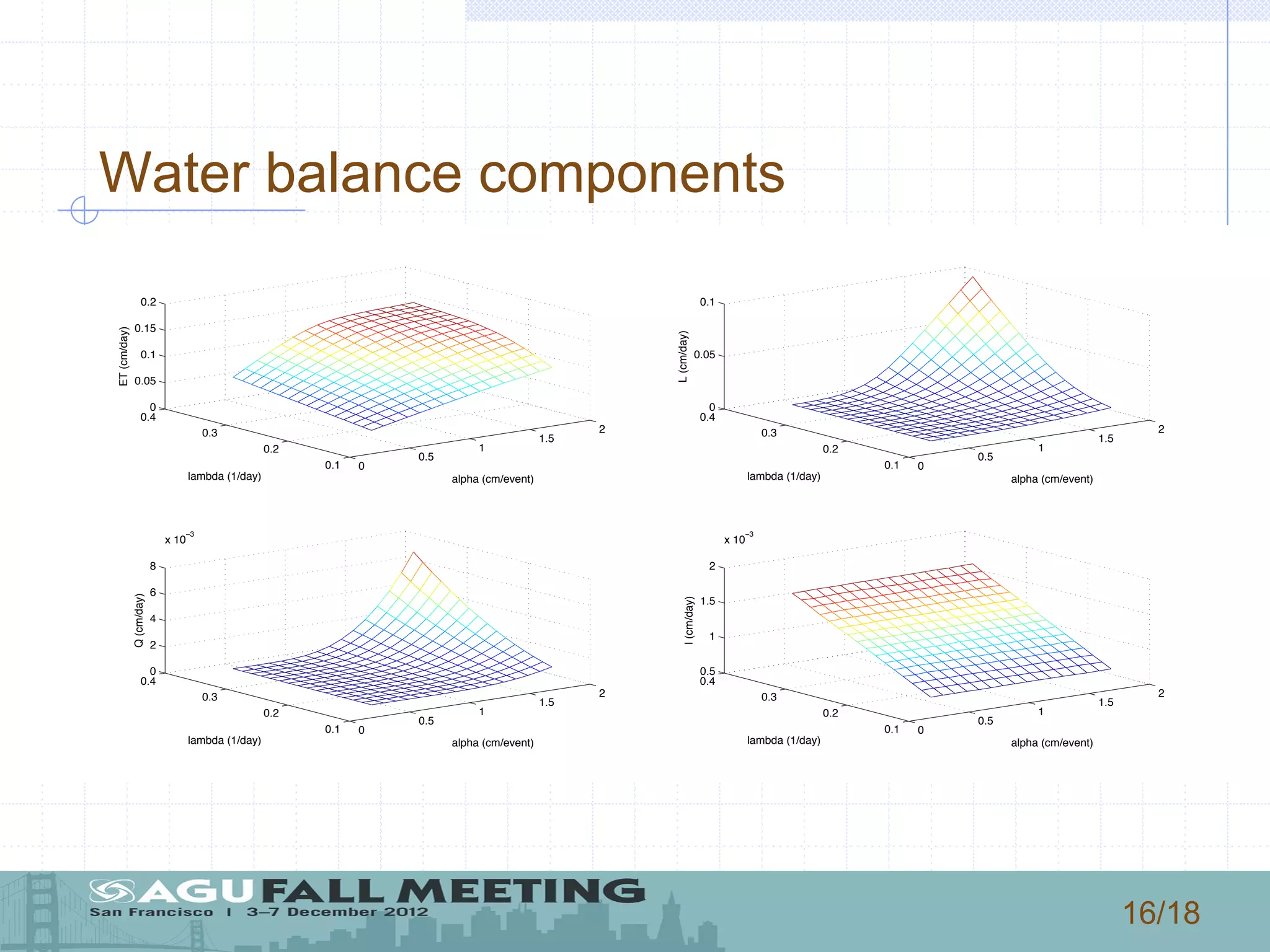
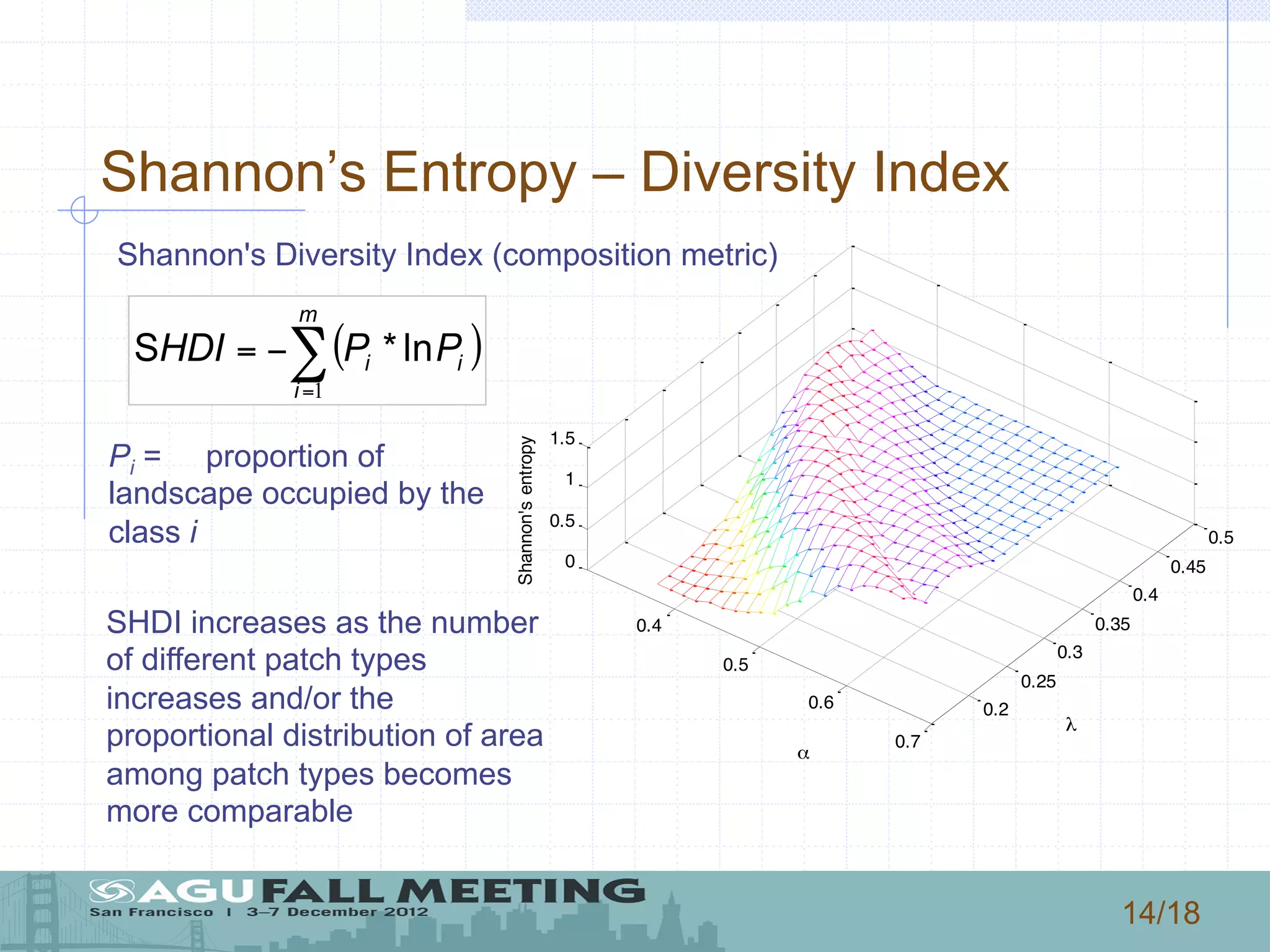
1) The document describes a model that couples patterns of vegetation, soil, and climate to generate patterns of water balance and soil moisture distribution within a basin in New Mexico. 2) The model uses a stochastic process to represent rainfall events and calculates water losses through evaporation, transpiration, and leakage to determine soil water balance. 3) The authors use the model to simulate how changes in rainfall characteristics, like rate and mean depth, could impact vegetation patterns, landscape diversity, and the water balance components of evapotranspiration, leakage, runoff, and infiltration.

1. 1/18
Salvatore Manfreda1, Teresa Pizzolla1, Kelly K. Caylor2
1) University of Basilicata, Italy.
2) Princeton University, USA.
EFFECTS CLIMATE CHANGE ON WATER
RESOURCES AVAILABILITY AND VEGETATION
PATTERNS
e-mail salvatore.manfreda@unibas.it

2. 2/18
Motivation
Global precipitation projections for
December, January, and February (top
map) and June, July, and August (bottom
map.) Blue and green areas are projected
to experience increases in precipitation by
the end of the century, while yellow and
pink areas are projected to experience
decreases.
Source: Christensen et al. (2007)
How climate change will impact
on vegetation patterns?
How this will modify water
resources?

3. 3/18
Modelling application
Upper Rio Salado
Catron County, NM
Cibola National Forest
Basin Area: 681 km2
Mean Annual Rainfall: 218±84 mm
Sevilleta LTER
(Caylor et al., AWR 2005)

4. 4/18
! Couple patterns of vegetation, soil, and climate to generate patterns of
steady state water balance and soil moisture distribution within the basin
! Use existing stochastic model of soil moisture:
( ) ( )sts
dt
ds
nZr χϕ −= ,
Input is a poisson process of
rainfall events with a characteristic
distribution of storm depths
(Rodriguez-Iturbe et al., 1999; Laio
et al., 2001; Manfreda et al, 2010)
Losses are determined according to a loss
function that includes
evaporation, transpiration, and leakage
0
0.5
1
1.5
2
2.5
3
3.5
0 s
h
s
w s* s
fc 1
χ(s)cm/d
E
max
E
vap
Soil Water balance

5. 5/18
Basin Water Stress Profile
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
0
0.2
0.4
0.6
0.8
1
x
θʹ′
1.0
0.0
⎪
⎩
⎪
⎨
⎧
<
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
otherwise
kTTif
kT
T
seass
n
seas
s
s
1
'
'
*
*
*
/1
ζ
ζ
θ
t
s(t)
Duration of the growing season, Tseas
ξ
Duration of an excursion
below ξ
(Porporato et al., AWR – 2001)
Dynamic water stress defined
as a function of frequency of
crossing, number of crossing,
mean time of crossing, etc.

6. 6/18
Dynamics of organization within river
networks
Initial
Condition
Neighbor model:
Interactions can occur between all 8 neighbors
Network model:
Interactions constrained by flow path – only
downstream neighbors can be replaced
2
1
Cells replace neighbor pixels if it lowers
the local amount of water stress with a
probability p
How well do each of these interactions
represent the observed distribution of water
stress?
(Caylor et al., GRL 2004)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−=
21
1
1
θθ
θ
p
Cell becomes bare when θ is 1 for all
vegetation types

7. 7/18
Neighbor Model
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
0
0.2
0.4
0.6
0.8
1
x
θʹ′
Network model
Actual
Steady-state condition
Model calibration

8. 8/18
Potential
evapotranspiration
Rn = Ra 1−α( )−εsσTs
4
+εaσTa
4
Rdir
Rdif Rem
αRdir
Rrif
Ra
atmosphere
target
Ra =
GSC
d2 cos θ( )dω
ω1
ω2
∫
Net solar radiation

9. 9/18
DWS Tree
km
km
1 10 20 30 40 50 60 70 80 90 100
1
10
20
30
40
50
60
70
80 0
0.2
0.4
0.6
0.8
1
DWS Shrub
km
km
1 10 20 30 40 50 60 70 80 90 100
1
10
20
30
40
50
60
70
80 0
0.1
0.2
0.3
0.4
DWS Grass
km
km
1 10 20 30 40 50 60 70 80 90 100
1
10
20
30
40
50
60
70
80 0
0.2
0.4
0.6
0.8
1
DWS Tree
km
km
1 10 20 30 40 50 60 70 80 90 100
1
10
20
30
40
50
60
70
80 0
0.2
0.4
0.6
0.8
1
DWS Shrub
km
km
1 10 20 30 40 50 60 70 80 90 100
1
10
20
30
40
50
60
70
80 0
0.1
0.2
0.3
0.4
0.5
DWS Grass
km
km
1 10 20 30 40 50 60 70 80 90 100
1
10
20
30
40
50
60
70
80 0
0.2
0.4
0.6
0.8
1
T! s! = T!!
s! −T! s +
1
ν s
−
1
ν s!
+γ
1
ν u
!−T! u
!!
!
du
θ′ =
T!"#! −T! s!
T!"#!
θ
Dynamic water stress
Dynamic water stress computed
including initial conditions
The mean first passage time (in
days) of the stochastic process
between s0 (initial condition) and
<s>
Basin morphology modifies dynamic
water stress allowing the existance of
some spiecies.

10. 10/18
Vegetation pattern obtained including the
effects of morphology on solar radiation
Initial
Condition
Cells replace neighbor pixels if it
lowers the local amount of water
stress with a probability p
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−=
21
1
21
1
1
TT
T
p
θθ
θ
Vegetation strategy is:
• to minimize of stress
• and maximize transpiration

11. 11/18
Ecohydrological Model: Simulation Results
200 400 600 800 1000 1200
100
200
300
400
500
600
700
800
900
1000
(Hurvitz, 2002)
The proposed model has been used to predict 256 scenario defined
changing both the mean rainfall rate (λ) and the mean rainfall depth (α).
Increasing mean annual rainfall

12. 12/18
Land Cover Changes with Rainfall Characteristics
(rainfall rate λ and mean depth α)
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.1
0.2
0.3
0.4
0.5
0
20
40
60
80
λα
Treecover(%)
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.1
0.2
0.3
0.4
0.5
0
20
40
60
λα
ShrubCover(%)
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.1
0.2
0.3
0.4
0.5
0
20
40
60
λα
Grasscover(%)
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.1
0.2
0.3
0.4
0.5
0
50
100
λα
Baresoil(%)

13. 13/18
Metrics of Landscape Ecology
Landscape Ecology Metrics allow these patterns in space to be described
quantitatively:
§ Quantification of patch configuration on the landscape
§ Central quantitative basis for much analysis & understanding in
Landscape Ecology
§ Attempt to quantify either individual patches, classes, or the entire
landscape
§ Assess continuity, contiguity, fragmentation and diversity of landscape
elements
(from Fragstats manual)
Landscape metrics

14. 14/18
Shannon’s Entropy – Diversity Index
0.4
0.5
0.6
0.7
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0
0.5
1
1.5
λ
α
Shannon'sentropy
( )∑=
−=
m
i
ii PPHDI
1
ln*S
SHDI increases as the number
of different patch types
increases and/or the
proportional distribution of area
among patch types becomes
more comparable
Pi = proportion of
landscape occupied by the
class i
Shannon's Diversity Index (composition metric)

15. 15/18
Same rainfall with different rate or mean
depth
10 12 14 16 18 20 22 24 26 28 30
0
0.2
0.4
0.6
0.8
1
1.2
1.4
α λ Ts
[cm]
Shannon'sentropy
λ =0.224
λ =0.299
λ =0.374
λ =0.449
α =0.428
α =0.503
α =0.578
α =0.653
…changes in α provides sharper modifications of landscape.
LandscapeDiversity
Annual rainfall
Changing α
Changing λ

16. 16/18
Water balance components
0
0.5
1
1.5
2
0.1
0.2
0.3
0.4
0
0.05
0.1
0.15
0.2
alpha (cm/event)lambda (1/day)
ET(cm/day)
0
0.5
1
1.5
2
0.1
0.2
0.3
0.4
0
0.05
0.1
alpha (cm/event)lambda (1/day)
L(cm/day)
0
0.5
1
1.5
2
0.1
0.2
0.3
0.4
0
2
4
6
8
x 10
−3
alpha (cm/event)lambda (1/day)
Q(cm/day)
0
0.5
1
1.5
2
0.1
0.2
0.3
0.4
0.5
1
1.5
2
x 10
−3
alpha (cm/event)lambda (1/day)
I(cm/day)

17. 17/18
Water balance components
0
0.5
1
1.5
2
0.1
0.2
0.3
0.4
40
60
80
100
alpha (cm/event)lambda (1/day)
ET(%)
0
0.5
1
1.5
2
0.1
0.2
0.3
0.4
0
10
20
30
40
alpha (cm/event)lambda (1/day)
L(%)
0
0.5
1
1.5
2
0.1
0.2
0.3
0.4
0
1
2
3
alpha (cm/event)lambda (1/day)
Q(%)
0
0.5
1
1.5
2
0.1
0.2
0.3
0.4
0.5
1
1.5
2
2.5
3
alpha (cm/event)lambda (1/day)
I(%)

18. 18/18
Conclusions
! Spatial distribution of vegetation is mainly controlled by local climate
and the basin morphology that plays a dual role influencing the local
climatic forcing on one hand and the amount of incoming radiation
on the other.
! Network structure constrains spatial interactions in catchments, with
important consequences on the evolution of spatial patterns within
the river basins.
! The landscape analysis, based on the modeling applications, show
that reduction of landscape diversity may occur rapidly for small
changes in the rainfall characteristics.
! These changes are exacerbated when rainfall modifications are due
to reduction in the mean rainfall depth.
! In semiarid environment vegetation pattern evolves maximizing
water use and most of the rainfall is transformed in
evapotranspiraton.

19. 19/18
Thanks for your attention…