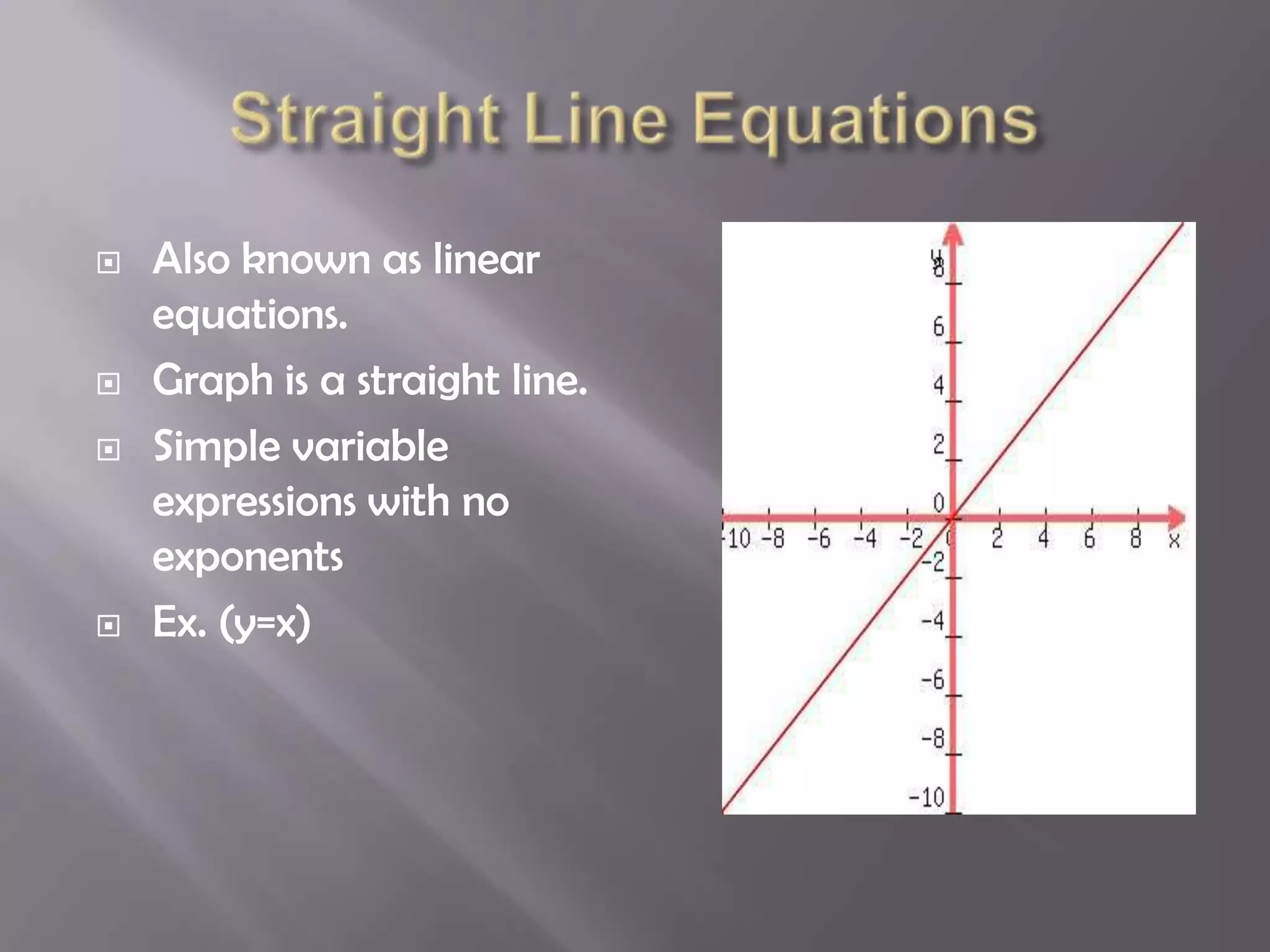
The document discusses linear equations and their two main forms - slope-intercept form (y=mx+b) and point-slope form (y-y1=m(x-x1)). It explains how to use each form to find the equation of a line given values for the slope and/or a point on the line. Examples are provided for finding linear equations using both forms.

1. Johnny Jones
EDU 290
11:00am

2.  Also known as linear
equations.
 Graph is a straight line.
 Simple variable
expressions with no
exponents
 Ex. (y=x)

3. SLOPE-INTERCEPT FORM POINT-SLOPE FORM
 Format used to solve the  The format used when
equation of a line in the slope is given along
relation to the slope and with a point along the
y-intercept. line.
 y=mx+b  (y-y1)= m(x-x1)

5.  The slope-intercept form is y=mx+b
 m stands for the slope of the line
 y is the output of the equation
 b is the y-intercept at which x=0
 x is the input of the equation

6.  Using the formula y=mx+b,
 Usually every variable, except for one, is given and
you have to solve for the remaining variable.
 The most dominant variables that need to be
solved for are x and y.
 But sometimes this can also include the slope and
y-intercept.

7.  Find the equation for  Find the equation of
the line where the the line where the
slope=2 and the y- slope=1/2 and the point
intercept= -4. given is (3,-2)
 Plug in the  Plug in the
givens, y=mx+b givens, y=mx+b
 y=2(0)+(-4)  -2=1/2(3)+b
 y=-4  -2=3/2+b
 -7/2=b

9.  y is the output of the equation at any point along the
line
 y1 is the output of a given point
 m is the slope
 x is the input of the equation at any point along the
line
 x1 is the input of a given point

10.  Using the formula y-y1=m(x-x1),
 Plug in any givens and solve for unknowns
 In the case that there is more than one
unknown, solve for y.

11.  Find the equation of  Find the equation of
the line with a slope of the line where the
2 and passes through slope=1/2 and the point
the point (2,0). given is (3,-2)
 y-y1=m(x-x1)  y-y1=m(x-x1)
 y-0=2(x-2)  y+2=(1/2)(x-3)
 y=2x-4  y+2=(x-3/2)
 y=(x-3/2)-2

14.  Find the equation for the line where the slope=2
and the y-intercept= -4.
 Find the equation of the line where the slope=1/2
and the point given is (3,-2)

15.  y=mx+b
 -4=2(0)-4
-4=-4
 -2=(3/2)-(7/2)
-2=(-4/2)
-2=-2

16.  Find the equation of the line with a slope of 2 and
passes through the point (2,0).
 Find the equation of the line where the slope=1/2
and the point given is (3,-2)

17.  y-y1=m(x-x1)
 0=2(2)-4
0=4-4
0=0
 -2=(3-3)/2-2
-2=(0/2)-2
-2=-2

18.  The 1st graph
http://www.algebra.com/algebra/homework
/quadratic/Quadratic_Equations.faq.question.
233197.html
 The content
purplemath.com
 The last two graphs
webgraphing.com