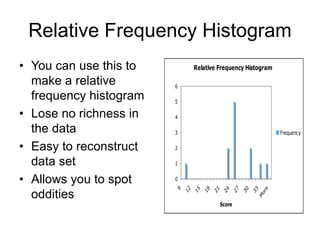
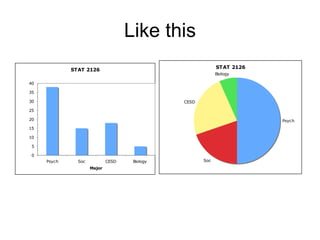
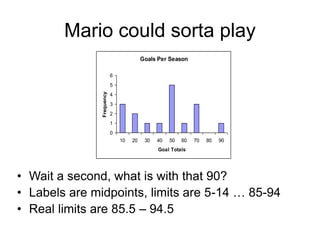
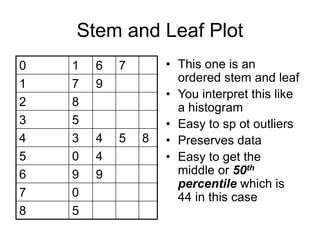
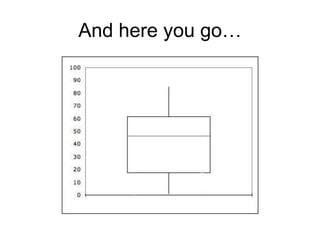
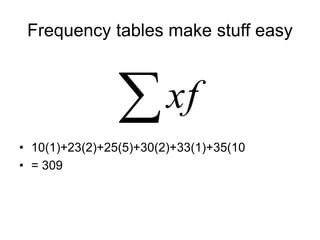This document provides an introduction to exploratory data analysis (EDA). It explains that EDA, developed by John Tukey, allows researchers to understand their data, find patterns and outliers, generate hypotheses without losing richness. Different techniques are demonstrated for different data types, including histograms, bar graphs, and stem-and-leaf plots to visualize quantitative and categorical variables, and identify distributions, central tendency, spread, and outliers. Care must be taken to ensure scales are appropriate. The five number summary and boxplots are also introduced.