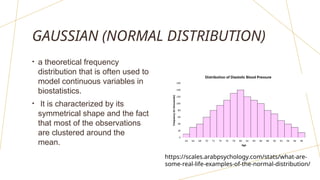
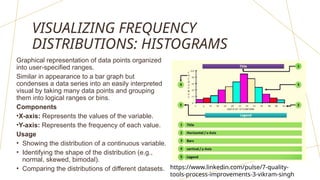
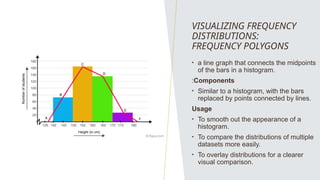
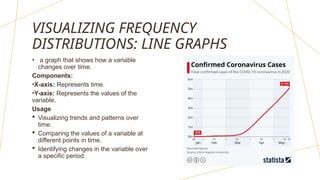
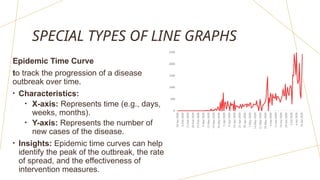
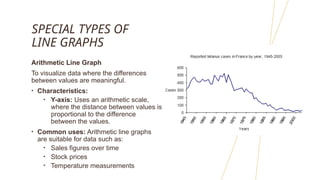
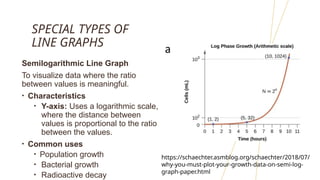
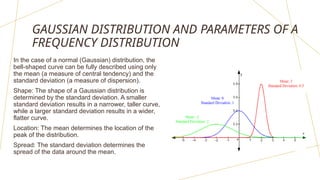
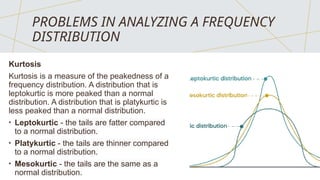
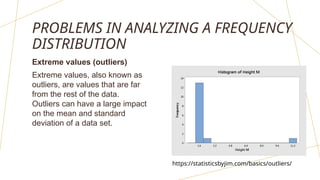
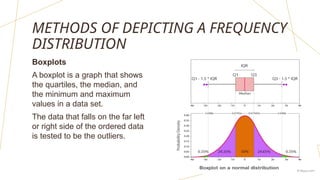
The document discusses frequency distributions of continuous variables, explaining the difference between real and theoretical distributions, along with the Gaussian distribution's characteristics. It covers methods for visualizing data, such as histograms, frequency polygons, and line graphs, along with key parameters like measures of central tendency and dispersion. The text also highlights potential issues in analysis, including skewness, kurtosis, and the impact of outliers.