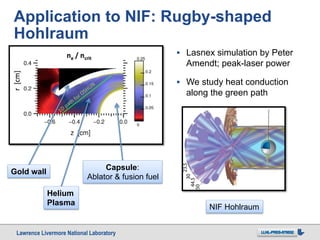
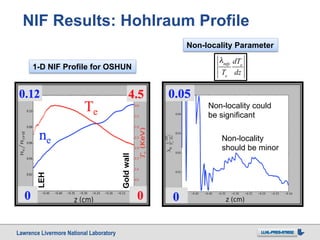
This work uses a Fokker-Planck (OSHUN) code to model electron heat conduction in National Ignition Facility (NIF) hohlraums. Clinical tests with OSHUN show significant non-local reduction in thermal conductivity for steep temperature gradients compared to the Spitzer-Härm theory. Application to 1D NIF hohlraum profiles in OSHUN demonstrates non-local reduction in the entrance hole region and heat flux exceeding Spitzer-Härm inside the hohlraum, possibly due to reflecting boundaries. Future work will include modeling return current instabilities, 2D simulations, and realistic gold wall conditions.

1. LLNL-PRES-XXXXXX
This work was performed under the auspices of the U.S. Department
of Energy by Lawrence Livermore National Laboratory under contract
DE-AC52-07NA27344. Lawrence Livermore National Security, LLC
Fokker-Planck Modeling of Heat
Conduction in NIF Hohlraums
HEDP Summer Student Presentation
25 August 2015
LLNL-PRES-676532

2. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
2
Thanks to
• Andy Cook and Summer Student Program
• D. J. Strozzi (LLNL) – mentor
• A. Tableman, B. Winjum (UCLA) – much help with OSHUN
• I. Heinz (LLNL) – computer support

3. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
3
Motivation
§ Electron heat conduction: long-standing issue in inertial fusion and
laser-produced plasmas
§ Local treatment for collision-dominated, short mean-free-path
plasma: Spitzer and Härm, Phys. Rev. 1953
§ Heat flux reduced from Spitzer-Härm by:
• Non-locality: electrons with v=(2-4) thermal speed carry flux.
Less collisional than thermals. Become “de-localized,” no net flux
• Return current instability: bulk electrons drift relative to ions
— Triggers ion-acoustic instability
— Recent interest on NIF and Omega: C. Thomas, M. Rosen
• Magnetic fields: reduce heat flux across field
( )
3
... heat flux thermal conductivity
2
e e e
d
n T T
dt
κ κ= ∇ ⋅ + ≡ ∇ = ≡Q Q

4. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
4
Relevance to NIF
§ Understanding heat flux is crucial to understanding ICF experiments
§ Electron Flux Limit f
• Traditional “kludge” to match experimental data:
§ Pre-2009, low (x-ray) flux model
• XSN atomic physics
• f=0.05
§ Post-2009, high flux model (M. Rosen et al., High Energy Density
Physics, 2011) to match NIF data
• DCA atomic physics
• f=0.15
Q = min{ f *ne
me
vTe
3
, QSpitzer−H!!arm
}
Goal of this work:
Fokker-Planck modeling of heat flux in NIF hohlraums

5. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
5
Kinetic Theory
§ Distribution function: f(x, v) = density of particles at phase-space
location (x, v)
§ Boltzmann equation: governs evolution of f for weak particle
correlations (for experts: f2 = f1* f1 molecular chaos assumption)
§ Fokker-Planck equation: small-angle scattering limit of
Boltzmann equation
§ Collisions entail many, small, independent momentum kicks,
e.g. weakly-coupled plasma (fails for strong coupling)
∂f
∂t
+ v⋅∇f +
q
m
E+
v×B
c
⋅∇v f =
δ f
δt collisions
δ f
δt collisions
= −
∂
∂v
⋅ f Δv%& '(+
1
2
∂
∂v
∂
∂v
: f ΔvΔv%& '(

6. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
6
§ Developed by M. Tzoufras, maintained at UCLA by Prof. W. Mori’s
group
§ We use 1D relativistic Python version, kinetic electrons, fixed ions:
§ Spherical harmonic expansion in velocity space:
§ Collision Operators:
• Electron-ion: immobile ions; pitch-angle scattering, or Lorentz gas:
damping rate increases with L mode number
• Electron-electron (self collisions): included, complicated…
OSHUN: Vlasov-Fokker-Planck code
∂fe
∂t
+ v⋅∇fe −
eE
me
⋅∇v fe = Cee +Cei
v = v(cosϕ sinθ,sinϕ sinθ,cosθ)fe (r,v,t) = fl
m
m=−l
l
∑ (r,v,t)Pl
m
(cosθ)eimϕ
l=0
∞
∑
δ f
δt collisions
=υpa
∂µ
(1−µ2
)∂µ
f#
$
%
& → Cei
[ fl
m
]=
δ fl
m
δt ei
= −l(l +1)
ni
Γei
2v3
fl
m
E = E(z)ˆz

7. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
7
§ Fluid variables: velocity moments of distribution
§ Fluid equations: moments of Boltzmann equation
Fluid Description, e.g. rad-hydro codes
Number density: n = f d3
∫ v
Drift velocity: u =
1
n
v∫ f d3
v
Temperature: T =
m
3n
| v − u |2
∫ f d3
v
Heat Flux: Q = (v − u)
m
2
| v − u |2
f d3
∫ v
Continuity Equation (n=0):
∂n
∂t
+ ∇⋅(nu) = 0
Momentum Transfer Equation (n=1): mn
∂
∂t
+ v⋅∇
$
%
&
'
(
)v = qn(E+ v×B)− ∇p+ R
Energy Transfer Equation (n=2):
∂
∂t
nmv2
2
+
3nkT
2
$
%
&
'
(
)− nqE⋅v + ∇⋅Q =
∂
∂t
nmv2
2
$
%
&
'
(
)
collisions
vn
f d3
v∫
Subject of
this work

8. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
8
Spitzer-Härm Theory of Heat Flux
§ Local theory: mean free path << gradient scale lengths
§ Diffusive approximation: keep L=0,1:
§ Linearize f1 << f0, steady state d/dt=0, neglect e-e collisions here:
§ Steady-state: E field develops, so no net current
0 1
2
0 3/2
1 1
( , ) ( , ) ( , )
( , ) exp / 2 Maxwellian, ( ), ( ) vary in z
( , ) ( )cos
e
e e e e
e
f z f v z f z
n
f v z m v T n z T z
T
f z F v θ
= +
⎡ ⎤∝ −⎣ ⎦
=
v v
v
0 0
1z
z
f feE
v f
z m v
υ
∂ ∂
− ≅
∂ ∂
1
0
5
0
2
e e e
e
T dn dTE
J E
t en dz e dz
ε −∂
= − = → = − −
∂

9. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
9
Spitzer-Härm heat flux carried by electrons
with vz = (2-4)x thermal speed
f0
f1
f0 + f1
qz0
qz0 + qz1
qz1
( )z x yf dv dv f= ∫ v
2
( )
2
z
x y z
z
q m
dv dv v v f
v
∂
=
∂ ∫ v
eT∇
Heat flux from f0(vz > 0) and f0(vz < 0) cancel.
Heat flux from f1 symmetric à net flux = red curve

10. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
10
Clinical non-local test with OSHUN:
Epperlein-Short1 Test
§ Significant non-local reduction in thermal conductivity for steep
temperature gradients
§ Why is L = 1 different? Likely code setup issue in Python version
1E. Epperlein and R. Short, Phys. Fluids B (1991)
Spitzer-Härm result
Non-local
reduction in κ

11. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
11
Application to NIF: Rugby-shaped
Hohlraum
§ Lasnex simulation by Peter
Amendt; peak-laser power
§ We study heat conduction
along the green path
Capsule:
Ablator & fusion fuel
Helium
Plasma
Gold wall
NIF Hohlraum

12. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
12
NIF Results: Hohlraum Profile
1-D NIF Profile for OSHUN
Non-locality Parameter
λmfp
Te
dTe
dz
Non-locality
should be minor
Non-locality could
be significant
LEH
Goldwall

13. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
13
NIF Results: thermal conductivity
L = 2
L = 3
L = 4
Conductivity does not vary with
more L-modes
Spitzer-Härm Value
LEH:
Non-local
reduction
Gold wall:
Exceeds
Spitzer-Härm
Reflecting (non-periodic) boundaries
dx, dp, dt
dx/2, dp, dt
dx, dp/2, dt
dx, dp, dt/2
Grid size: Converged w.r.t. dx, dp
Slight dependence on dt

14. Lawrence Livermore National Laboratory LLNL-PRES-xxxxxx
14
Conclusions
• OSHUN gives well-known non-local reduction of heat conduction with
steep temperature gradients
• 1D OSHUN runs on NIF profiles:
• computationally cheap: less than 100 CPU-hours
• Non-local reduction in heat conductivity in entrance hole
• Exceeds Spitzer-Härm inside hohlraum - reflecting boundaries?
• Mobile ions: capability being developed in OSHUN
• Allow study of return current instability
• 2D simulations
• Gold wall conditions
Future Work