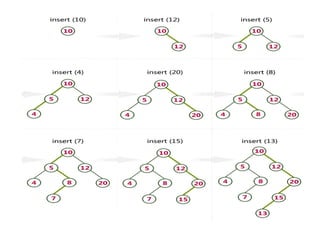
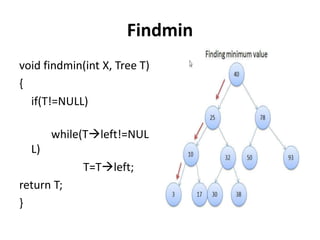
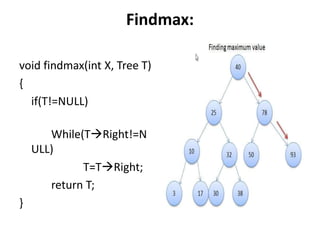
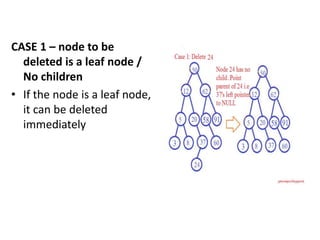
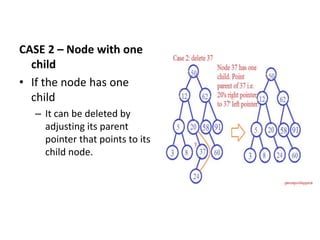
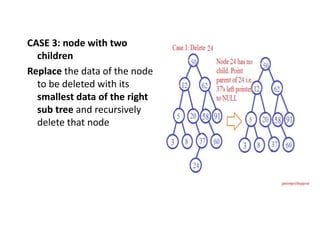
Binary search trees have nodes where the left child is less than the root and the right child is greater than the root. Nodes are inserted by traversing the tree recursively to find an empty spot. Values are found by recursively searching and comparing to the root. Minimum and maximum values are found by traversing all the way left or right. Nodes are deleted by case analysis on whether they have 0, 1, or 2 children and adjusting pointers or replacing with children accordingly.

1. Binary Search Trees
Definition:
Binary search tree is a binary tree in
which the key values in the left node is
less than the root and the key values in
the right node is greater than the root.

2. Struct treenode
{
int Element;
SearchTree Left;
SearchTree Right;
}

3. insert
• To insert the element X into the tree
– Check with the root node T
– If it is less than the root
• Traverse the left sub tree recursively until it reaches
The TLeft ==NULL.
• Then X is placed in T Left
– If X is greater than the root
• Traverse the right sub tree recursively until it reaches
The TrRght ==NULL.
• Then X is placed in T Right

5. Void insert(int X, Tree T)
{
If(T==NULL)
{
T=malloc(sizeof(struct TreeNode));
if(T!=NULL)
{
TElement= X
T Left = NULL
T Right =NULL
}
}
else if (X<TElement)
Tleft=insert(X,Tleft)
Else if(X>TElement)
Tright=insert(X,Tright)
}

6. Find
– Check the value X with the root node value
• If X is equal to T data, return T
• If X is less than T data, traverse the left of T
recursively
• If X is greater than T data, traverse the right of T
recursively

7. Find
void find(int x, tree t)
{
if(T==NULL)
return NULL
if (X<Telement)
return find(X,Tleft)
else if(X>TElement)
return find(X,Tright)
else
return T
}

8. Findmin
– start from root go left as long as there is left child.
– Returns the position of the smallest element in
the tree

9. Findmin
void findmin(int X, Tree T)
{
if(T!=NULL)
while(Tleft!=NUL
L)
T=Tleft;
return T;
}

10. Findmax
• Return the position of largest in the tree
• start from root go left as long as there is left child.

11. Findmax:
void findmax(int X, Tree T)
{
if(T!=NULL)
While(TRight!=N
ULL)
T=TRight;
return T;
}

12. CASE 1 – node to be
deleted is a leaf node /
No children
• If the node is a leaf node,
it can be deleted
immediately

13. CASE 2 – Node with one
child
• If the node has one
child
– It can be deleted by
adjusting its parent
pointer that points to its
child node.

14. CASE 3: node with two
children
Replace the data of the node
to be deleted with its
smallest data of the right
sub tree and recursively
delete that node

15. void delete(int X, Tree T)
{
if(T==NULL)
Error “No tree value”;
else if (X<T-->Element)
T--> Left = Delete(X,T--> Left)
else
if(X> T> T--> Element)
T--> Right = Delete(X, T--> Right)
else
if(T--> Left && T--> Right)
{
Tmpcell = FindMin (T-->Right)
T-->Element = Tmpcell-->Element
T-->Right = Delete(T-->Element; T-->Right)
}

16. else
{
Tmpcell =T
if(T-->Left == NULL)
T=T-->Right
else if(T-->Right==NULL)
T=T--> Left
free(Tmpcell);
}
return T
}