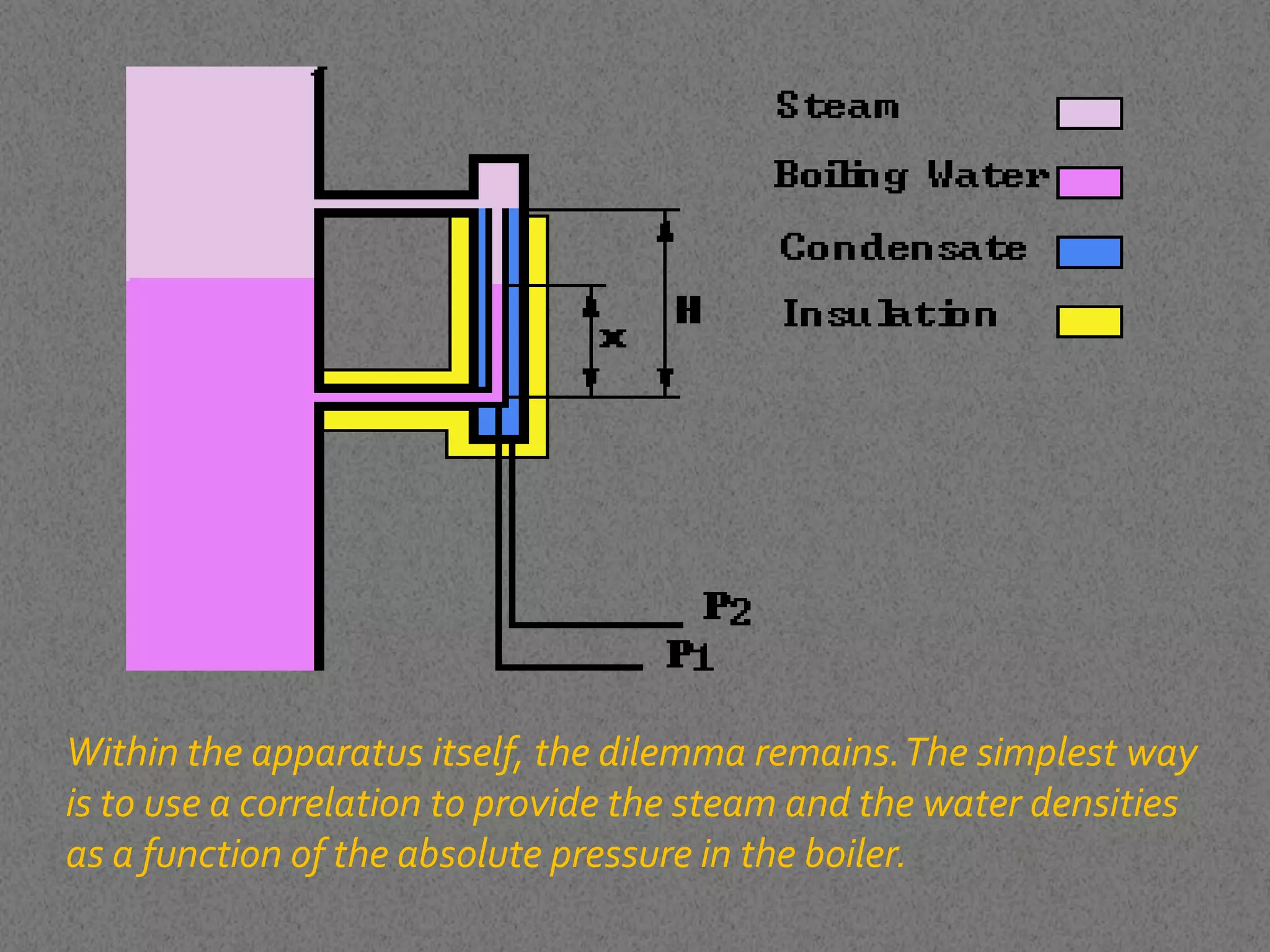
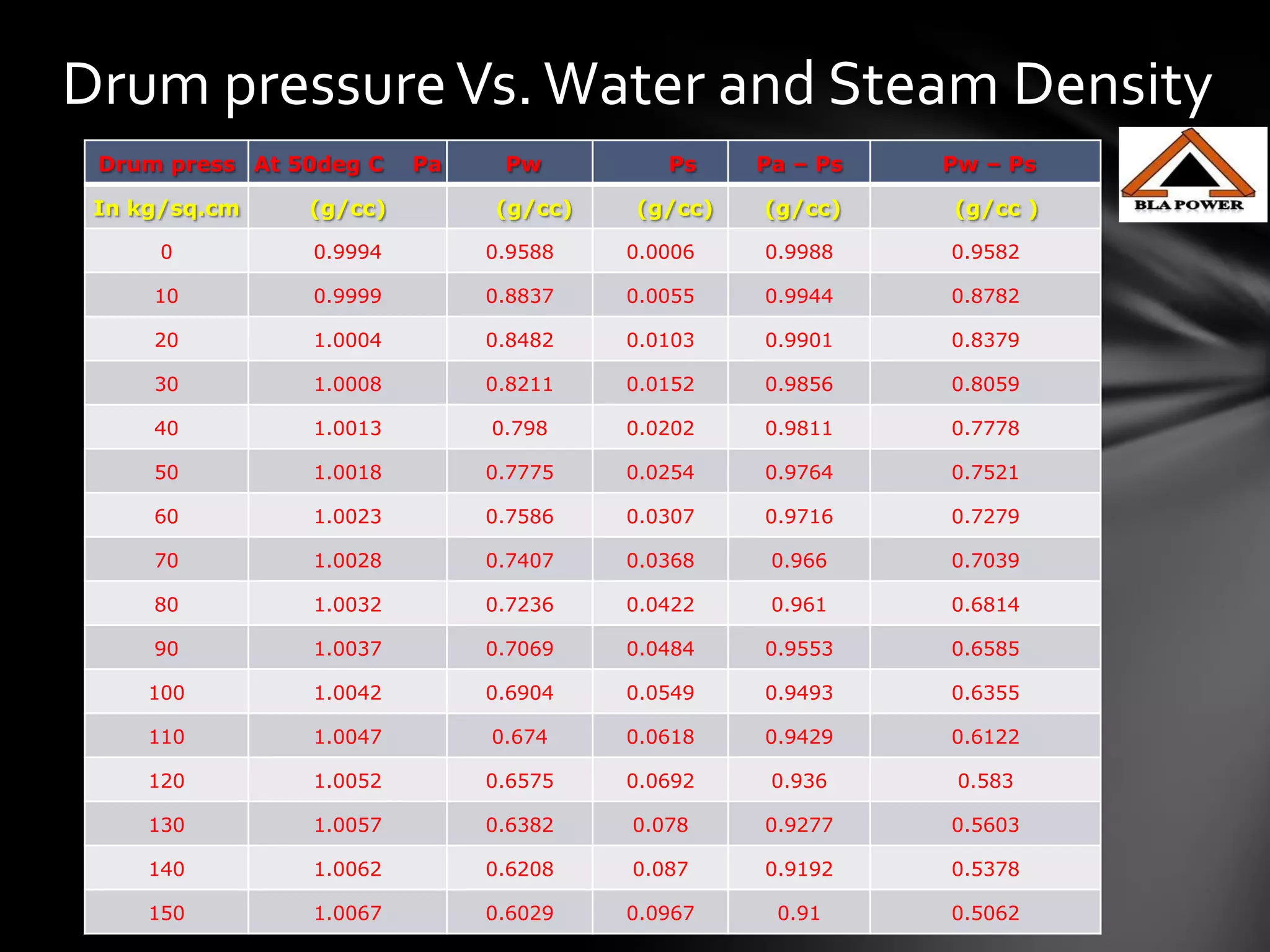
The level measurement in a steam drum is complex due to changing densities of water and steam with temperature. A level capture apparatus maintains a constant wet leg temperature by condensation to ensure consistent densities. The level can be calculated using a correlation of steam and water densities with pressure. The level percentage is determined by subtracting the raw transmitter output from 100%, divided by the difference between water and steam densities.

1. Lalit Singh
Control and Instrumentation

2. Steam drum level measurement with a differential pressure transmitter
can be a tricky business when the pressure is higher than for "low"
pressure steam. What happens is that as the temperature rises, the
density of water drops while at the same time that of steam rises. To
compound the problem, the wet leg temperature is not well defined and
its density is a third variable.
A technical way around the wet leg problem is to use the following level
capture apparatus. fig.. The constant condensation in the top
connection maintains a constant influx of hot water at equilibrium with
the steam. This maintains the heat and ensures both wet leg and
measurement sections are at the same temperature (that of the water in
the steam drum), below the apparatus, the two impulse lines are in close
contact and therefore at the same temperature. Whatever the density of
the water is, it is the same in both legs and cancels out in the differential
measurement
WHYTHE LEVEL MEASURENT IS
COMPLEX

3. Within the apparatus itself, the dilemma remains.The simplest way
is to use a correlation to provide the steam and the water densities
as a function of the absolute pressure in the boiler.

4. Looking at figure, we see that the differential pressure, P2 - P1 is:
∆P=g.(pw –ps). (H-X)
where g is the gravitational acceleration constant: 9.807 m/s2, and
pw =Is The Water Density at Operating Condition.
ps =Is The Steam Density at Operating Condition.
Furthermore we assume the transmitter is calibrated with cold water which has a
density of Pc=998.2 Kg/m3
We note that when the level is 100%, the differential pressure is 0, regardless of
whether the water is hot or cold. When the level is 0%, the differential pressure is
maximum although this maximum value depends on the pressure in the steam
drum. Now, assuming the transmitter has a reversed output, Lraw, calibrated with
cold water, so that when the level increases so does the analog signal, then it is
possible to express the level, L, in % as a function of the densities of the water
(both hot and cold) and of the steam:
L=100-(100-Lraw)/K , Where K= (pw –ps)/ Pc
Than L= 100-(100-Lraw)/ (pw –ps) ,Where Assuming Pc=1 g/cc
Formula Derive

5. Lvl = (dRefCol – dDrmStm – LvlIn * dTransWtr) / (dDrmWtr – dDrmStm)
Lvl = the percentage of the distance between the level measurement
taps of the water level above the lower level measurement tap –
expressed as 0 – 1.0.
dRefCol is the density of the reference column water
dDrmWtr is the density of the drum water
dDrmStm is the density of the drum steam
dTransWtr is the density of the transmitter calibration water
Lvl= (dRefCol – dDrmStm – LvlIn) / (dDrmWtr – dDrmStm)
Where dTransWtr= 1 g/cc
Formula in Our DCS

6. Lvl= 100(pa-ps)-(100-Dp%)
(pw-ps)
pw =Is The Water Density at Operating Condition.
ps =Is The Steam Density at Operating Condition.
pa=Is The wet Density.
Dp %= Raw value of Transmitter out put.
We are assuming here the drum pressure is 120 Kg/Cm2 and Dp
% is 30 %
Than pa-ps=0.936 and pw-ps=0.583
Lvl={100x0.936-(100-30)}/0.583
Lvl=40.48 %
How calculate the Level in DCS

7. L= 100-(100-Lraw)
(pw –ps)
We are assuming here the drum pressure is 120 Kg/Cm2 and Lraw
is 30 %
Than at 120 kg/cm2 ,pw-ps=0.583
L= 100-(100-30)
(0.583)
L=51.45 %
How to calculate the Level if wet leg
Density not Compensated

8. Calculation Of Level By IJT Formula
LEVEL SIGNAL AFTER PRESSURE COMPENSATION = {DP +(Pa-Ps)}/ (Pw-Ps)
PW = Water Density in gm/cc
PS = Steam Density in gm/cc
DP= LEVEL IN DP TRANSMITTER
Pa = Wet Leg Density in gm/cc
We are assuming here the drum pressure is 120 Kg/Cm2 and
Lraw is 30 % Than at 120 kg/cm2 ,pw-ps=0.583, pa-
ps=0.936
L =(30+0.936)/0.583
L=53.06

9. Drum press At 50deg C Pa Pw Ps Pa – Ps Pw – Ps
In kg/sq.cm (g/cc) (g/cc) (g/cc) (g/cc) (g/cc )
0 0.9994 0.9588 0.0006 0.9988 0.9582
10 0.9999 0.8837 0.0055 0.9944 0.8782
20 1.0004 0.8482 0.0103 0.9901 0.8379
30 1.0008 0.8211 0.0152 0.9856 0.8059
40 1.0013 0.798 0.0202 0.9811 0.7778
50 1.0018 0.7775 0.0254 0.9764 0.7521
60 1.0023 0.7586 0.0307 0.9716 0.7279
70 1.0028 0.7407 0.0368 0.966 0.7039
80 1.0032 0.7236 0.0422 0.961 0.6814
90 1.0037 0.7069 0.0484 0.9553 0.6585
100 1.0042 0.6904 0.0549 0.9493 0.6355
110 1.0047 0.674 0.0618 0.9429 0.6122
120 1.0052 0.6575 0.0692 0.936 0.583
130 1.0057 0.6382 0.078 0.9277 0.5603
140 1.0062 0.6208 0.087 0.9192 0.5378
150 1.0067 0.6029 0.0967 0.91 0.5062
Drum pressureVs.Water and Steam Density