The document discusses the investigation of quantum coherence in arrays of superconducting qubits, focusing on dynamic localization effects within these systems. It presents mathematical models and results demonstrating how oscillatory behaviors of current and mean-square displacement are influenced by specific parameters like electric field modulation and dephasing rates. Furthermore, it highlights the potential of using current measurements to estimate coherence and incoherence within the superconducting qubit chain.


![Dynamic localisation on infinite chain
Time-dependent Hamiltonian ( = 1)
H(t) = V
m=+∞
m=−∞
(σ+
mσ−
m+1 + σ−
mσ+
m+1
) −
m=+∞
m=−∞
(E0 + E1) cos(ωt)σ+
mσ−
m ,
V coupling strength between nearest-neighbours
σ±
m = (σx
m ± iσy
m)/2 acting on m-th site (σx
and σy
Pauli matrices)
E0 energy difference between adjacent sites, ω frequency
Mean-square displacement as function of E1 oscillates sinusoidally
Interaction picture → effective Hamiltonian with JE0
ω
Bessel function
Heff
I = V
m=+∞
m=−∞
JE0
ω
(
E1
ω
)(σ+
mσ−
m+1 + σ−
mσ+
m+1) ,
RESULTS [Dunlap&Kenkre, PRB (1986); Holthaus&Hone, Phil. Mag. B (1996)]
Argument of Bessel function is oscillatory function of time, with oscillation
frequency proportional to magnitude of electric field, i.e.
if E0 = nω, n ∈ R, and E1/ω is a zero of Bessel function J
then mean-square displacement oscillates sinusoidally ⇒ initially localised
particle remains localised ⇔ DYNAMICAL LOCALISATION
A. Liguori Probing quantum coherence in arrays of superconducting qubits](https://image.slidesharecdn.com/dpgtalkmarch2011-150314105234-conversion-gate01/75/DPG_Talk_March2011_AlexandraM_Liguori-3-2048.jpg)
![Dynamic localisation on infinite chain
Time-dependent Hamiltonian ( = 1)
H(t) = V
m=+∞
m=−∞
(σ+
mσ−
m+1 + σ−
mσ+
m+1
) −
m=+∞
m=−∞
(E0 + E1) cos(ωt)σ+
mσ−
m ,
V coupling strength between nearest-neighbours
σ±
m = (σx
m ± iσy
m)/2 acting on m-th site (σx
and σy
Pauli matrices)
E0 energy difference between adjacent sites, ω frequency
Mean-square displacement as function of E1 oscillates sinusoidally
Interaction picture → effective Hamiltonian with JE0
ω
Bessel function
Heff
I = V
m=+∞
m=−∞
JE0
ω
(
E1
ω
)(σ+
mσ−
m+1 + σ−
mσ+
m+1) ,
RESULTS [Dunlap&Kenkre, PRB (1986); Holthaus&Hone, Phil. Mag. B (1996)]
Argument of Bessel function is oscillatory function of time, with oscillation
frequency proportional to magnitude of electric field, i.e.
if E0 = nω, n ∈ R, and E1/ω is a zero of Bessel function J
then mean-square displacement oscillates sinusoidally ⇒ initially localised
particle remains localised ⇔ DYNAMICAL LOCALISATION
A. Liguori Probing quantum coherence in arrays of superconducting qubits](https://image.slidesharecdn.com/dpgtalkmarch2011-150314105234-conversion-gate01/75/DPG_Talk_March2011_AlexandraM_Liguori-4-2048.jpg)


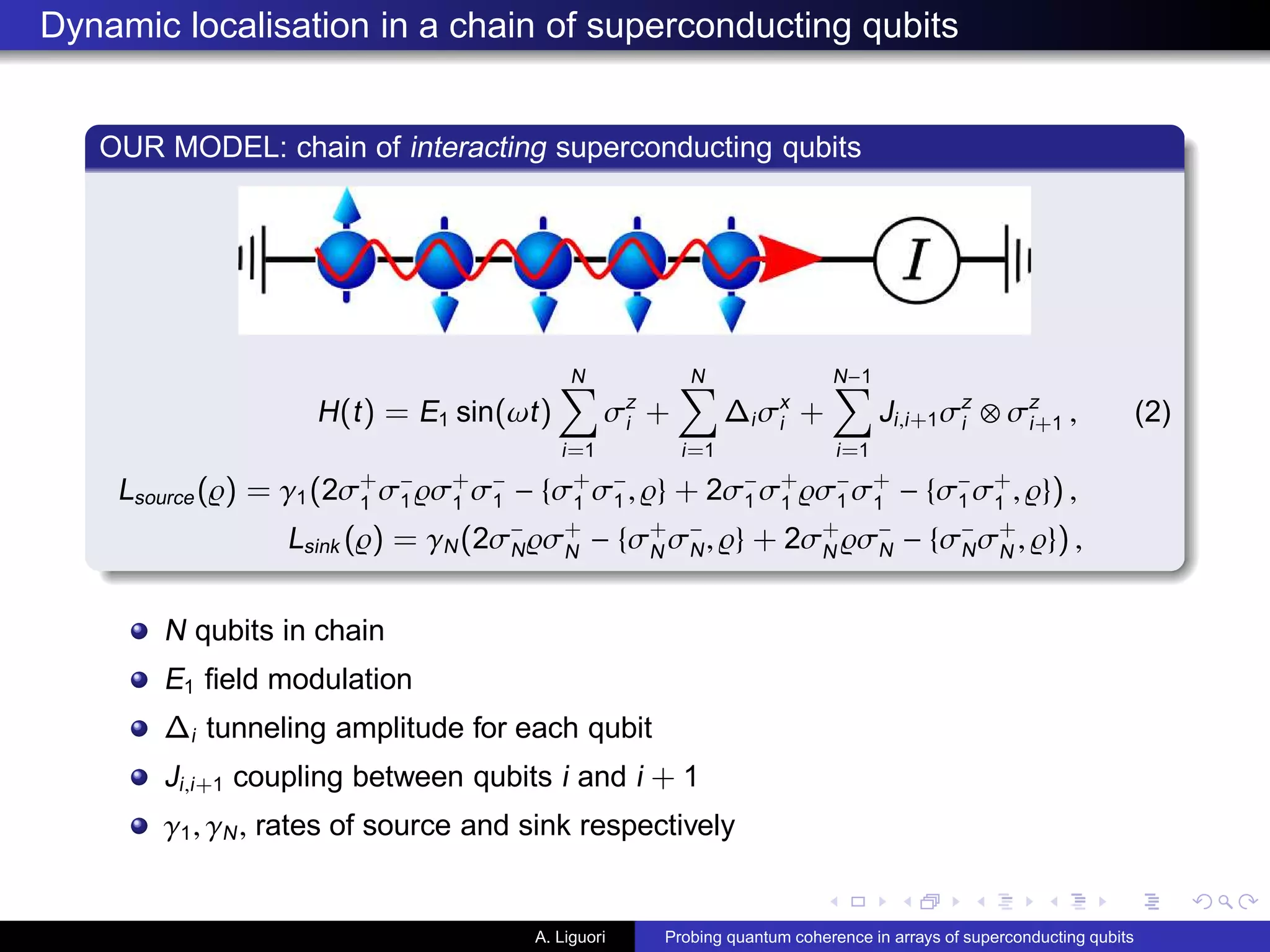
![Dynamic localisation in a chain of superconducting qubits
Quantum dynamical eq. for finite chain interacting with environment ( = 1)
d̺
dt
= −i[H, ̺] + Lsource(̺) + Lsink (̺) + Ldeph (̺)
with
Ldeph (̺) = γdeph
N
i=1
(2σ+
i
σ−
i ̺σ+
i
σ−
i − {σ+
i
σ−
i , ̺})
γdeph rate of dephasing noise.
Study current I as function of field modulation E1 in (2):
I = lim
t→∞
dpsink
dt
(t)
with psink (t) =
T
0
2γN̺N,N (t)dt, ̺N,N reduced density matrix of last site of chain.
A. Liguori Probing quantum coherence in arrays of superconducting qubits](https://image.slidesharecdn.com/dpgtalkmarch2011-150314105234-conversion-gate01/75/DPG_Talk_March2011_AlexandraM_Liguori-8-2048.jpg)
![Dynamic localisation in a chain of superconducting qubits
Quantum dynamical eq. for finite chain interacting with environment ( = 1)
d̺
dt
= −i[H, ̺] + Lsource(̺) + Lsink (̺) + Ldeph (̺)
with
Ldeph (̺) = γdeph
N
i=1
(2σ+
i
σ−
i ̺σ+
i
σ−
i − {σ+
i
σ−
i , ̺})
γdeph rate of dephasing noise.
Study current I as function of field modulation E1 in (2):
I = lim
t→∞
dpsink
dt
(t)
with psink (t) =
T
0
2γN̺N,N (t)dt, ̺N,N reduced density matrix of last site of chain.
A. Liguori Probing quantum coherence in arrays of superconducting qubits](https://image.slidesharecdn.com/dpgtalkmarch2011-150314105234-conversion-gate01/75/DPG_Talk_March2011_AlexandraM_Liguori-9-2048.jpg)
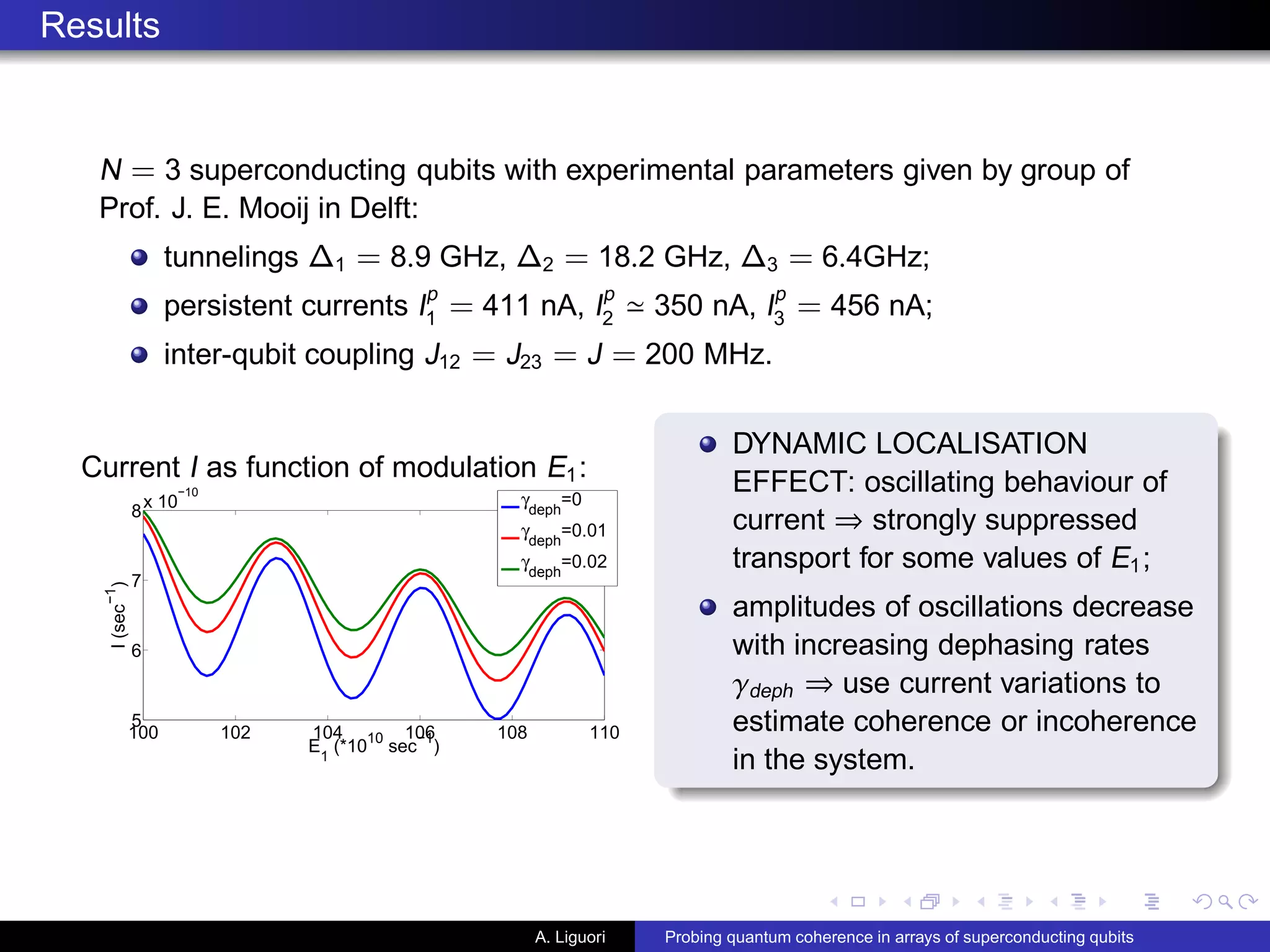
![5 5.2 5.4 5.6 5.8 6
6.7
6.8
6.9
7
7.1
7.2
I (sec*10
−10
)
C(*10
−4
) Incoherence measure C [Vaziri&Plenio,
New J. Phys. (2010)]:
C =
k l
|̺k,k ̺l,l − ̺k,l̺l,k |
⇒ C as function of I for given value of E1
at which first resonance can be found
Conclusions
1 DYNAMIC LOCALISATION IN SUPERCONDUCTING QUBIT CHAIN:
oscillating behaviour of current ⇒ strongly suppressed transport for some
values of E1;
2 amplitudes of oscillations decrease with increasing dephasing ⇒ use current
variations to estimate coherence or incoherence in the system;
3 (2) ⇒ incoherence measure C can be used as effective tool to estimate
presence of coherence in superconducting qubit chain by measuring current
I at fixed E1.
A. Liguori Probing quantum coherence in arrays of superconducting qubits](https://image.slidesharecdn.com/dpgtalkmarch2011-150314105234-conversion-gate01/75/DPG_Talk_March2011_AlexandraM_Liguori-11-2048.jpg)
![5 5.2 5.4 5.6 5.8 6
6.7
6.8
6.9
7
7.1
7.2
I (sec*10
−10
)
C(*10
−4
) Incoherence measure C [Vaziri&Plenio,
New J. Phys. (2010)]:
C =
k l
|̺k,k ̺l,l − ̺k,l̺l,k |
⇒ C as function of I for given value of E1
at which first resonance can be found
Conclusions
1 DYNAMIC LOCALISATION IN SUPERCONDUCTING QUBIT CHAIN:
oscillating behaviour of current ⇒ strongly suppressed transport for some
values of E1;
2 amplitudes of oscillations decrease with increasing dephasing ⇒ use current
variations to estimate coherence or incoherence in the system;
3 (2) ⇒ incoherence measure C can be used as effective tool to estimate
presence of coherence in superconducting qubit chain by measuring current
I at fixed E1.
A. Liguori Probing quantum coherence in arrays of superconducting qubits](https://image.slidesharecdn.com/dpgtalkmarch2011-150314105234-conversion-gate01/75/DPG_Talk_March2011_AlexandraM_Liguori-12-2048.jpg)