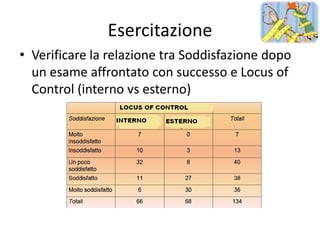
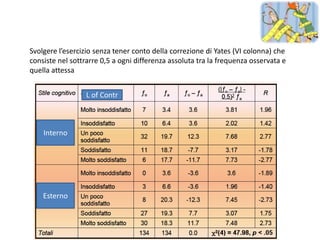
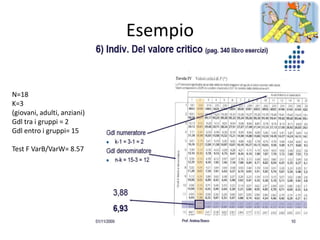
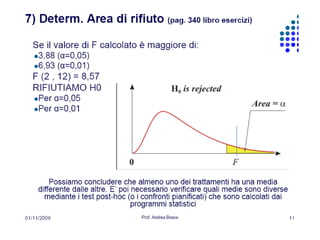
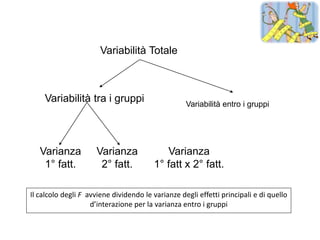
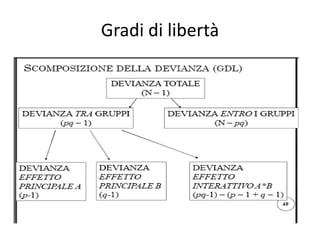
Il documento tratta della statistica inferenziale e dei vari test statistici utilizzati per verificare ipotesi sperimentali, come il test z, t, chi quadrato e F (ANOVA). Descrive come questi test confrontano le differenze tra campioni e popolazioni, stabilendo l'importanza di verificare la significatività statistica. Inoltre, discute le ipotesi nulla e alternativa, insieme all'uso delle tavole statistiche per determinare la probabilità che i risultati ottenuti siano dovuti al caso.


























































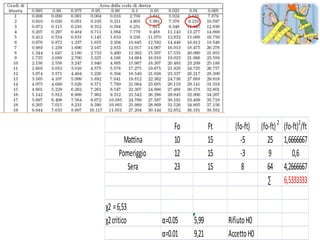



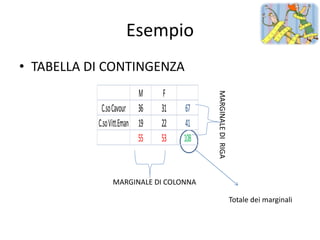

![Calcolo χ2
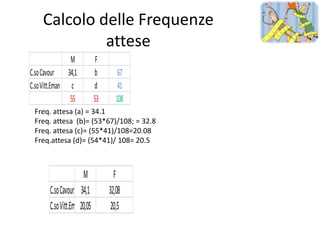
M F M F
C.so Cavour 36 31 67 C.so Cavour 34,1 32,08
C.so Vitt.Eman 19 22 41 C.so Vitt.Eman20,05 20,5
55 53 108
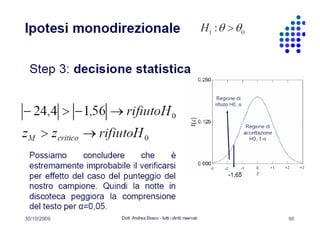
Χ2 =[(36-34,1) 2 /34,1 ]+[(31-32,8) 2 /32,8 ]+[(19-20,05) 2 /20,05]+[(22-20,5) 2 /20,5 ]
=0,34
Gdl= (c-1) *(r-1); 2
α=0.05
Χ2critico = 5.99 0,34<5,99; ACCETTO Ho](https://image.slidesharecdn.com/dott-ssapicuccistatisticainferenziale-111204151120-phpapp02/85/Dott-ssa-Picucci-Statistica-Inferenziale-75-320.jpg)