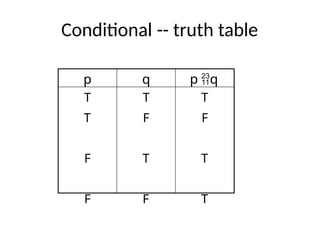
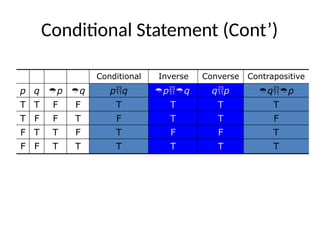
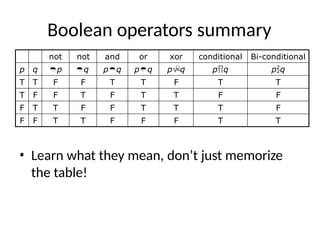
The document is a lecture on logic and proof in discrete mathematics, focusing on propositions and logical connectives. It covers types of propositions, the formation of compound propositions using operators like negation, conjunction, disjunction, and discusses conditional statements and their various forms. The lecture also includes examples of translating English sentences into logical expressions and the concept of truth tables for compound propositions.

1. Discrete Mathematics
Lecture 1: Logic and Proof
Lecturer: Suresh Khadka
February 08, 2023

3. Propositions
• A proposition is a statement that can be either
true or false
– “Yongdae has an Apple laptop.”
– “Yongdae is a professor.”
– “3 = 2 + 1”
– “3 = 2 + 2”
• Not propositions:
– “Are you Bob?”
– “x = 7”
– “I am heavy.”

4. Propositions (Cont.)
Are the following sentences propositions?
• Toronto is the capital of Canada. (Yes)
• Read this carefully. (No)
• 1+2=3 (Yes)
• x+1=2 (No)
• What time is it? (No)

5. Example :
Which of the following are propositions? Give the truth
value of the propositions.
a. 5 - 11 = 7.
b. Sydney is a city in Australia.
c. How do you do?
d. Look at the weather!

6. Propositional variables
• We use propositional variables to refer to
propositions
– Usually are lower case letters starting with p
(i.e.,
p, q, r, s, etc.)
– A propositional variable can have one of two
values: true (T) or false (F)
• A proposition can be…
– A single variable: p
– An operation of multiple variables:
p(qr)

7. Compound Propositions
In Propositional Logic, we assume a collection of
atomic propositions are given: p, q, r, s, t, ….
Then we form compound propositions by using
logical connectives (logical operators) to form
propositional “molecules”.

8. Logical Connectives
Operator Symbol Usage
Negation  not
Conjunction  and
Disjunction  or
Exclusive or  xor
Conditional  if,then
Biconditiona
l
 iff

9. Compound Propositions:
Examples
p = “Cruise ships only go on big rivers.”
q = “Cruise ships go on the Hudson.”
r = “The Hudson is a big river.”
r = “The Hudson is not a big river.”
pq = “Cruise ships only go on big rivers and go on
the Hudson.”
pq r = “If cruise ships only go on big rivers and
go on the Hudson, then the Hudson is a big river.”

10. Logical operators: Not
• A “not” operation switches (negates) the truth
value
• Symbol:  or ~
• p = “Today is not Friday”
p p
T F
F T

11. Logical operators: And (Conjunction)
• An “and” operation is true if both operands
are true
• Symbol: 
• pq = “Today is Friday
and today is my birthday”
p q pq
T T T
T F F
F T F
F F F

12. Conjunction
EG. p = “Clinton was the president.”
q = “Monica was the president.”
r = “The meaning of is is important.”
Assuming p and r are true, while q false.
Out of pq, pr, qr
only pr is true.

13. Logical operators: Or (Disjunction)
• An “or” operation is true if either operands
are true
• Symbol: 
• pq = “Today is Friday
or today is my birthday
(or possibly both)”
p q pq
T T T
T F T
F T T
F F F

14. Compound Statement (Example)
p = “It is hot” q = “It is sunny”
It is hot and sunny
It is not hot but sunny
It is neither hot nor sunny

15. Exclusive-Or – truth table
p q p q
T
T
F
T
F
T
F
T
T
Let p and q be propositions. The exclusive or of p and q,
denoted by p  q, is the proposition that is true
when exactly one of p and q is true and is false otherwise.

16. Conditional Statements
1.
A conditional statement is a statement that
can be expressed in “if-then” form.
2. A conditional statement has two
parts . The hypothesis is the “if”
part. The conclusion is the “then”
part.

17. Conditional Statements
Example:
(Original)
(Conditional)
I breathe when I sleep
If I am sleeping, then I
am breathing.

18. Conditional (Implication)
A conditional statement is also called an implication.
Example: “If I am elected, then I will lower taxes.”
p→ q
implication:
elected, lower taxes.
not elected, lower taxes.
T T | T
F T |
T
not elected, not lower taxes. F F |
T elected, not lower taxes. T F |
F

19. Conditional -- truth table
p q p q
T
T
F
F
T
F
T
F
T
F
T
T

20. Conditional Statement (Cont’)
Example:
Let p be the statement “Maria learns discrete mathematics.”
and q the statement “Maria will find a good job.” Express the
statement p→q as a statement in English.
Solution: Any of the following -
• “If Maria learns discrete mathematics, then she will find a
good job.
• “Maria will find a good job when she learns discrete
mathematics.”
• “For Maria to get a good job, it is sufficient for her to learn
discrete mathematics.”

21. Conditional Statements
To fully analyze this conditional statement, we
need to find three new conditionals:
Converse
Inverse
Contrapositiv
e

22. Conditional Statements
• The converse of a conditional statement is
formed by switching the hypothesis and the
conclusion.
• Example:
(Conditional)
(Converse)
If I am sleeping, then I
am breathing.
If I am breathing, then I am
sleeping.

23. Conditional Statements
• The inverse of a conditional statement
is formed by negating (inserting “not”) the
hypothesis and the conclusion.
• Example:
(Conditional) If I am sleeping, then I
am breathing.
(Inverse) If I am not sleeping, then
I am not breathing.

24. Conditional Statements
• The contrapositiv_e_ of a conditional statement is
formed by negating the hypothesis and the
conclusion of the converse.
• Example:
(Converse) If I am breathing, then I am
sleeping.
(Contrapositive) If I am not breathing,
then I am not sleeping.

25. Conditional Statements
Conditional
( if…then )
If I am sleeping, then I am
breathing.
Inverse
( insert not )
If I am not sleeping, then I am
not breathing.
Converse
( switch )
If I am breathing, then I
am sleeping.
Contrapositive
( switch and
insert not
)
If I am not breathing, then I am
not sleeping.

26. Conditional Statement (Cont’)
Converse of p→q: q→p
Contrapositive of p→q: ¬ q→¬ p
Inverse of p→q: ¬ p→¬ q

27. • Write the
– a) inverse
– b) converse
– c) contrapositive
If there is snow on the ground, then flowers are
not in bloom.
a) If there is no snow on the ground, then flowers are in
bloom.
b) If flowers are not in bloom, then there is snow on the
ground.
c) If flowers are in bloom, then there is no snow on the
ground.

28. Conditional Inverse Converse Contrapositive
p q p q pq pq qp qp
T T F F T T T T
T F F T F T T F
F T T F T F F T
F F T T T T T T
Conditional Statement (Cont’)

29. Logical operators: Bi-conditional 1
• A bi-conditional means “p if and only if q”
• Symbol: 
• Alternatively, it means
“(if p then q) and
(if q then p)”
• Note that a bi-conditional
has the opposite truth values
of the exclusive or
p q pq
T T T
T F F
F T F
F F T

30. Logical operators: Bi-conditional 2
• Let p = “You take this class” and q = “You get a
grade”
• Then pq means
“You take this class if
and only if you get a
grade”
• Alternatively, it
means “If
you take this class,
then
you get a grade and
if you get a grade
then
p q pq
T T T
T F F
F T F
F F T

31. Boolean operators summary
• Learn what they mean, don’t just memorize
the table!
not not and or xor conditional Bi-conditional
p q p q pq pq pq pq pq
T T F F T T F T T
T F F T F T T F F
F T T F F T T T F
F F T T F F F T T

32. Truth Tables of Compound
Propositions
We can use connectives to build up
complicated compound propositions involving
any number of propositional variables, then
use truth tables to determine the truth value
of these compound propositions.

33. Truth Tables of Compound
Propositions
Example: Construct the truth table of the
compound proposition : (pν ¬q) →(p Λ q).
(p Λ q)
p q ¬q p ν ¬q p Λ q (p ν ¬q)
→
T T F T T T
T F T T F F
F T F F F T
F F T T F F

34. Example
Construct the truth table of [~ (p Λ q)] V
r.

35. p q r p Λ q ~ (p Λ q) [~ (p Λ q)] V r
T T T T F T
T T F T F F
T F T F T T
T F F F T T
F T T F T T
F T F F T T
F F T F T T
F F F F T T

36. Precedence of Logical Operators
• We can use parentheses to specify the order
in which logical operators in a compound
proposition are to be applied.
• To reduce the number of parentheses, the
precedence order is defined for logical
operators.

37. Precedence of Logical Operators.
Operator Precedence
¬ 1
Λ 2
V 3
→ 4
↔ 5

38. Precedence of Logical Operators.
E.g. ¬p Λ q = (¬p ) Λ q
p Λ q V r = (p Λ q ) V r
p V q Λ r = p V (q Λ r)

39. Translating English Sentences
– p = “It is below freezing”
– q = “It is snowing”
• That it is below freezing is necessary and
sufficient for it to be snowing
pq
p¬
q
¬p
¬q
pq
p→q
• It is below freezing and it is snowing
• It is below freezing but not snowing
• It is not below freezing and it is not snowing
• It is either snowing or below freezing (or both)
• If it is below freezing, it is also snowing
p↔q

40. Translation Example
• “I have neither given nor received help on this
exam”
• Let p = “I have given help on this exam”
• Let q = “I have received help on this exam”
• ¬p¬q

41. Translating English Sentences
English (and every other human language) is
often ambiguous. Translating sentences into
compound statements removes the ambiguity.
How can these English sentences be
translated into a logical expression?
“You cannot ride the roller coaster if you are
under 4 feet tall unless you are older than 16
years old.”

42. Translating English Sentences
Solution: Let q, r, and s
q. represent “You can ride the roller coaster,”
r. “You are under 4 feet tall,” and
s. “You are older than 16 years old.”
The sentence can be translated into:
(r Λ ¬ s) → ¬q

43. Translating English Sentences
“You can access the Internet from campus only if
you are a computer science major or you are
not a freshman.”
Solution: Let a, c, and f represent “You can
access the Internet from campus,” “You are a
computer science major,” and “You are a
freshman.” The sentence can be translated
into: a  (c   f)

44. Bit Operations
• Boolean values can be represented as 1 (true)
and 0 (false)
• A bitstring is a series of Boolean
values. Length of the string is the number of
bits.
– 10110100 is eight Boolean values in one string
• We can then do operations on these Boolean
strings
– Each column is its own
Boolean operation
01011010
10110100
11101110